了解定时任务
我们在开发系统的时候,常常会遇到需要定时的去执行一些业务,例如:定时备份数据库、定时生成报告、定时发送通知、定时批处理等各种自动化操作。
那此时我们就需要通过使用定时任务来完成这些业务需求。并且在日常的开发中定时任务可以提高系统的效率、自动化重复性操作,极大程度上减少了人工工作量。
定时任务种类
常见的定时任务分别有Timer,ScheduledThreadPoolExecutor(定时任务线程池),Spring Task,Quartz,elastic-job……
在这么多的定时任务中,基本上都是两种理论基础实现的,分别是:小顶堆算法和时间轮算法
其中Timer,ScheduledThreadPoolExecutor(定时任务线程池),Spring Task都是基于小顶堆算法实现的
Quartz,elastic-job包括还有一些更为复杂的定时任务大部分都是基于时间轮算法实现的
(PS:Spring Task 中的@Scheduled注解严格意义上并不能说是基于小顶堆算法,@Scheduled主要是依赖于Spring框架中的ThreadPoolExecutor的TaskScheduler作为默认的任务调度器实现。它会根据指定的任务触发规则,将定时任务封装成一个Runnable,然后提交给线程池执行。但是TaskScheduler的底层实现是ThreadPoolTaskScheduler,它使用了ScheduledThreadPoolExecutor作为线程池。所以说它虽然没有直接使用小顶堆算法,但是底层使用了基于小顶堆算法的ScheduledThreadPoolExecutor,我这边就把他归为小顶堆了)
接下来就开始介绍小顶堆
小顶堆
了解小顶堆之前,我们首先要了解堆
堆是一种特殊的树,只要满足以下两个条件,它就是一个堆:
- 堆是一颗完全二叉树
- 堆中某个节点的值总是不大于(或不小于)其父节点的值
其中,根节点最大的堆叫做大顶堆,根节点最小的对叫做小顶堆
满二叉树:所有层都达到最大节点数
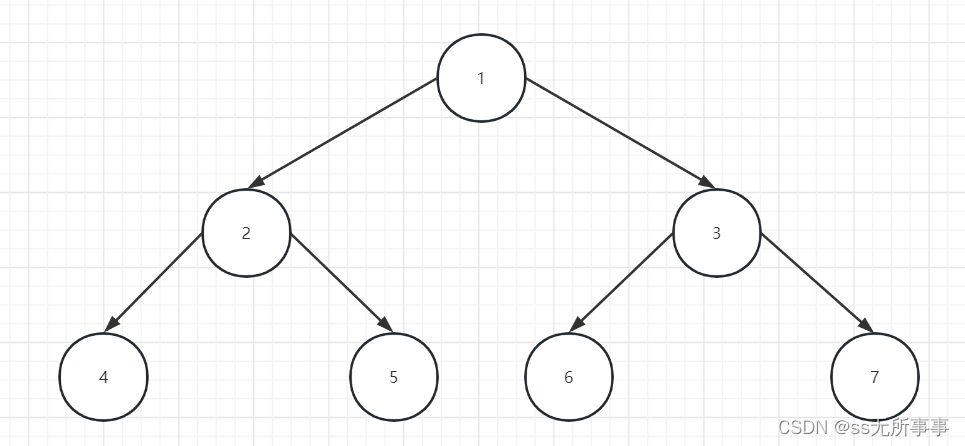
完全二叉树:除了最后一层外其他层达到最大节点数,且最后一层节点都靠左排列
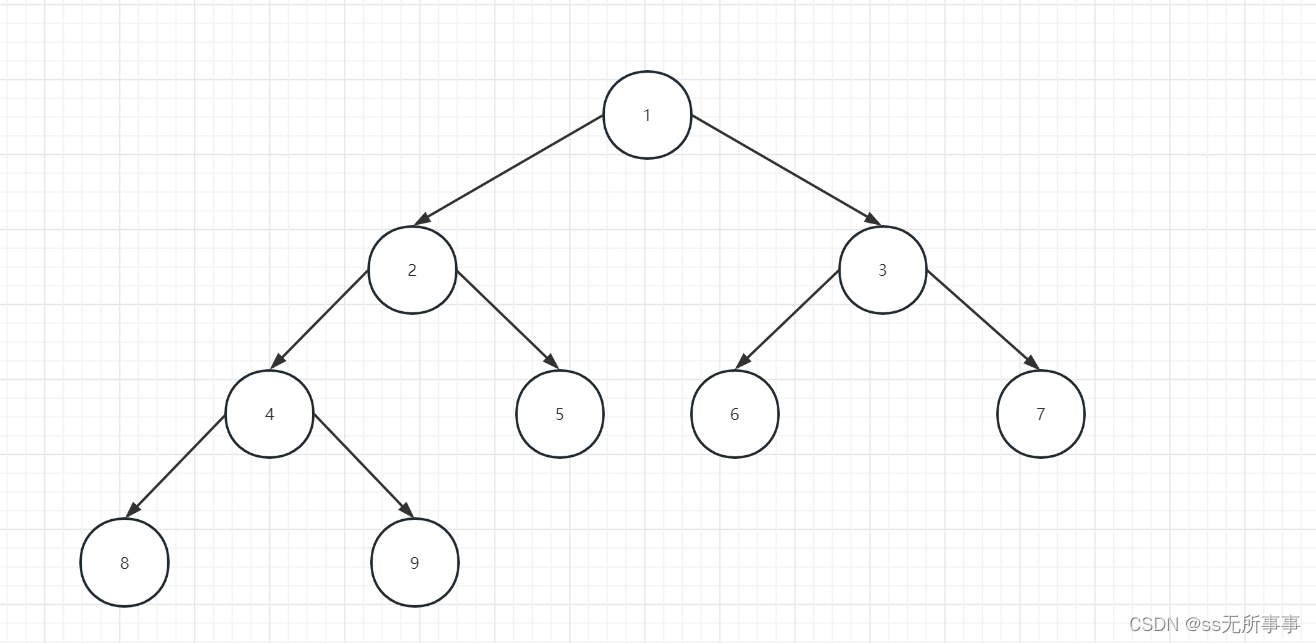
完全二叉树最适合用数组作为存储,因为它的节点都是紧凑的,并且只有最后一层节点数不满

为什么0节点不存储数据呢?
这是为了让我们可以更快更方便的去找到它的父节点(只需要将其下标除2),例如5的父节点就是5/2=2,6的父节点就是6/2=3,它们父节点的位置一目了然。
那我们的定时任务和这个堆又有什么关系呢?
实际上我们的定时任务每一个任务(Job)都对应这我们堆里的一个节点,就相当于每个节点都存放着一个Job。
那Job是如何存放的呢,难道是随便放吗?
实际上是Job的存放顺序是基于我们小顶堆的特性:最顶上的元素是最小的,这个就对应着我们定时任务的过期时间,最短的就放在最上面。当时间到了之后就直接去取对顶的元素执行就好了。堆顶元素执行之后,那下一次定时任务又改如何去拿呢?这个就需要取了解堆的存取元素的方法
插入元素
8字真言:尾部插入,然后上浮
为什么要从尾部插入,从顶部插入不行吗?
答:如果从顶部插入的话,如果顶部存在其他元素,就需要将所有的元素都往后移一位,而从尾部插入元素的话就不存在移位的操作。
插入元素后不一定满足堆的特性,为了继续满足堆的特性,我们就需要堆化。
样例:
往这个堆里插入元素2,我们把它放在9的后面,但是此时它并不满足(堆中某个节点的值总是不大于(或不小于)其父节点的值)这个条件,于是我们就需要将其进行堆化
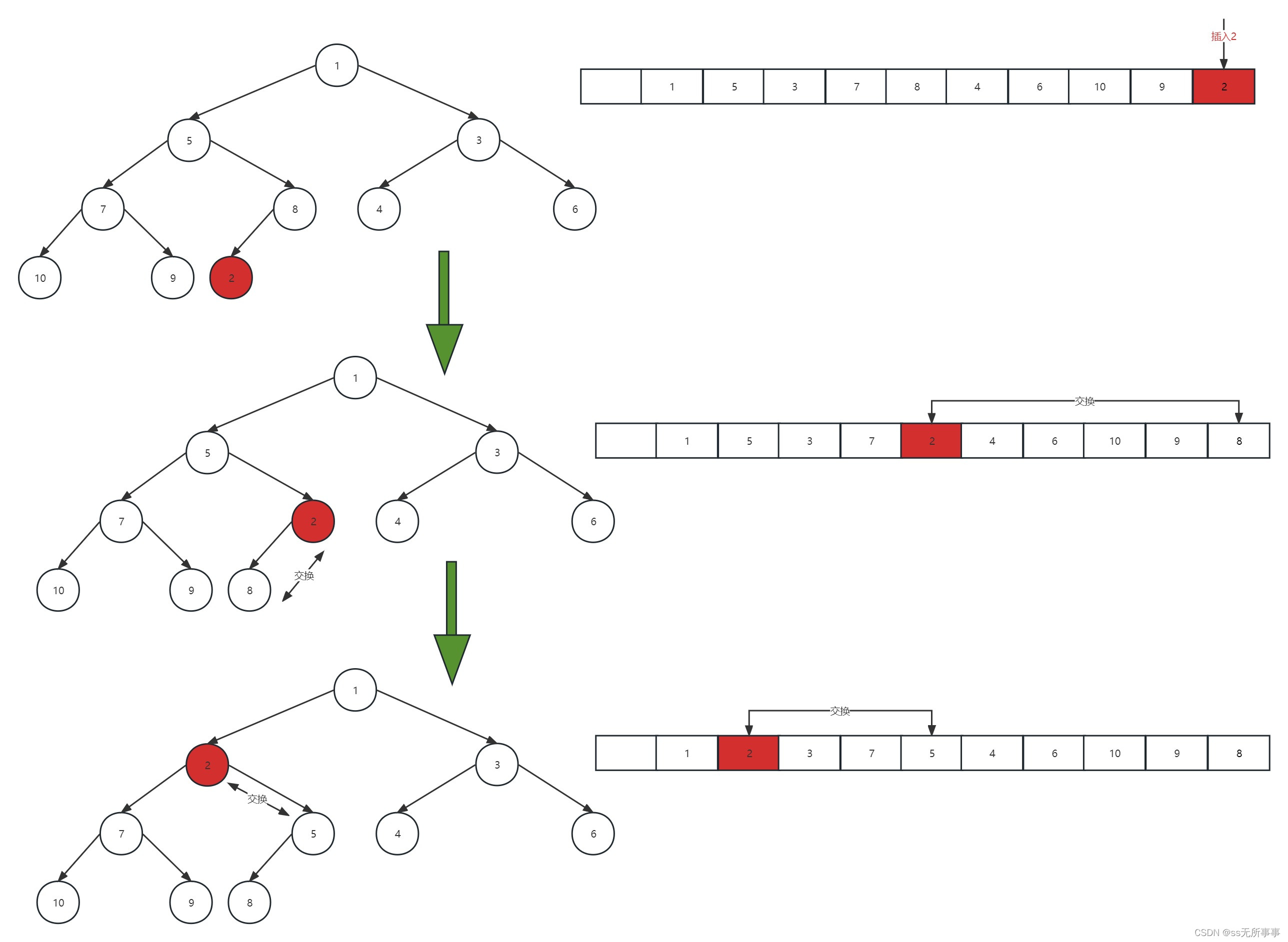
在完全二叉树中,插入的节点与它的父节点相比,如果比父节点小,就交换他们的位置,交换后再比较再交换,直到它比父节点大为止。
这就是插入元素时进行的堆化,也叫自下而上的堆化。
删除元素
!记住只能删除堆顶的元素
尾部(最大的元素)放到堆顶,然后下沉
如果小顶堆中堆顶存储是最小的元素,这时候我们把它删除会怎么样呢?
删除元素后,我们需要继续满足堆的特性,首先先把最后一个元素移到根节点的位置,这个就满足了第一个条件(完全二叉树),之后就是满足另一个父节点大于子节点的条件,于是我们就需要进行堆化。
示例:
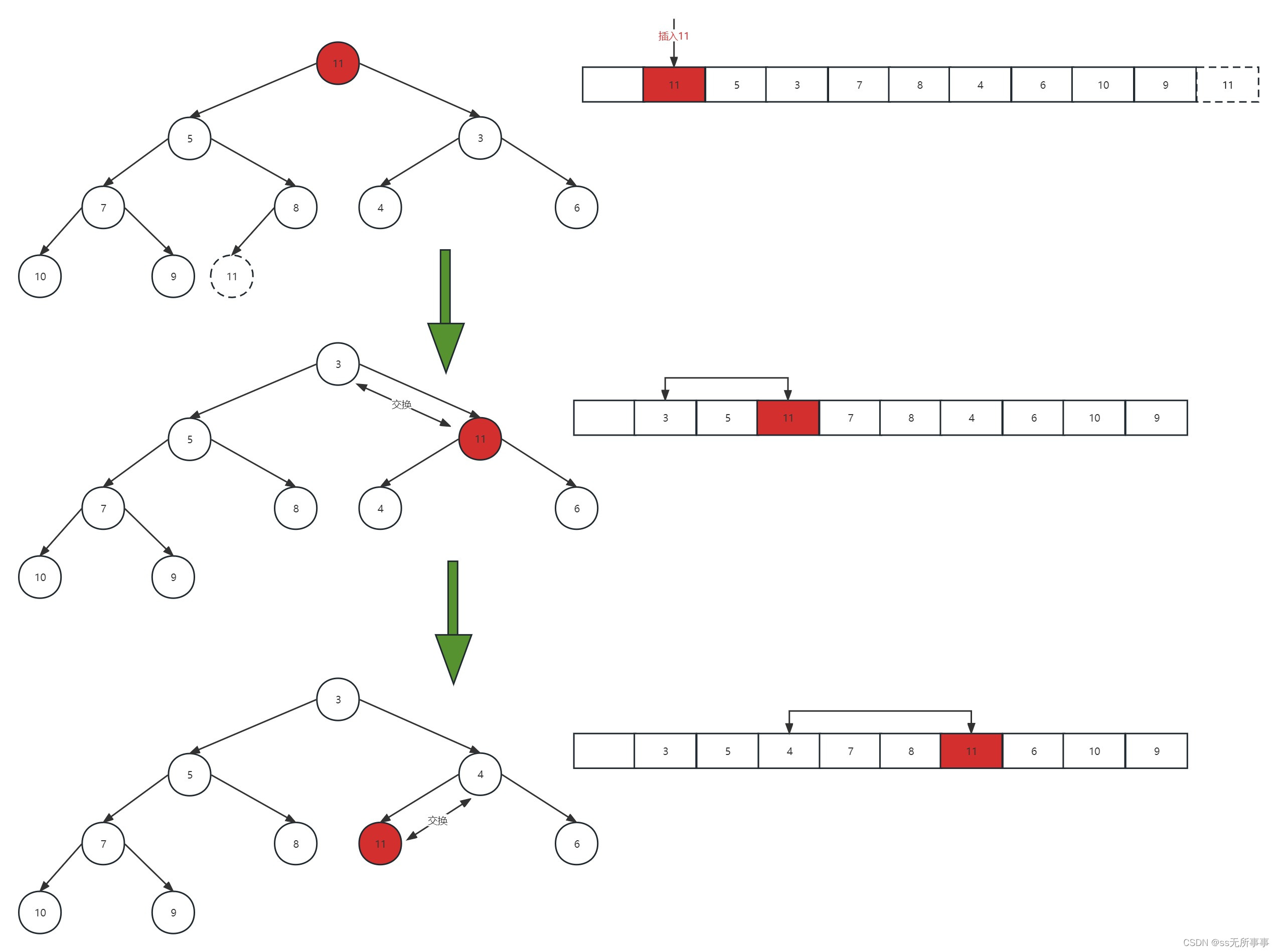
在完全二叉树中,把最后一个节点放到堆顶,然后与左右子节点中最小的节点交换位置依次往下,直到比左右子节点都小为止(或者没有子节点)。
这就是删除元素时进行的堆化,也叫自上而下的堆化。
这就是小顶堆理论的具体实现逻辑,接下来我们看时间轮算法
时间轮算法
时间轮算法其实就是由链表或者数组实现的:while-true-sleep:遍历数组,每个下标放置一个链表,链表节点放置任务,遍历到了就取出执行
很多人会好奇,为什么有了小顶堆又要用时间轮取实现呢?
实际上小顶堆是有弊端的,例如删除顶堆元素,如果此时我们的节点数过多,就需要进行大量的下沉操作,而我们定时任务的执行又是一个很平凡的时间,这样就会很耗费性能。
并且还有一个问题,例如顶堆的任务执行之后,按小顶堆的理论是需要将最尾端的节点放到顶端再一步一步进行下沉,此时就会出现一个问题:例如今天是1号,我尾端的任务是3号才执行,那我有必要把尾端的节点放到顶部再一步一步比对下沉吗?
这两种情况都会导致大量的性能浪费
所以此时就需要时间轮算法
简述
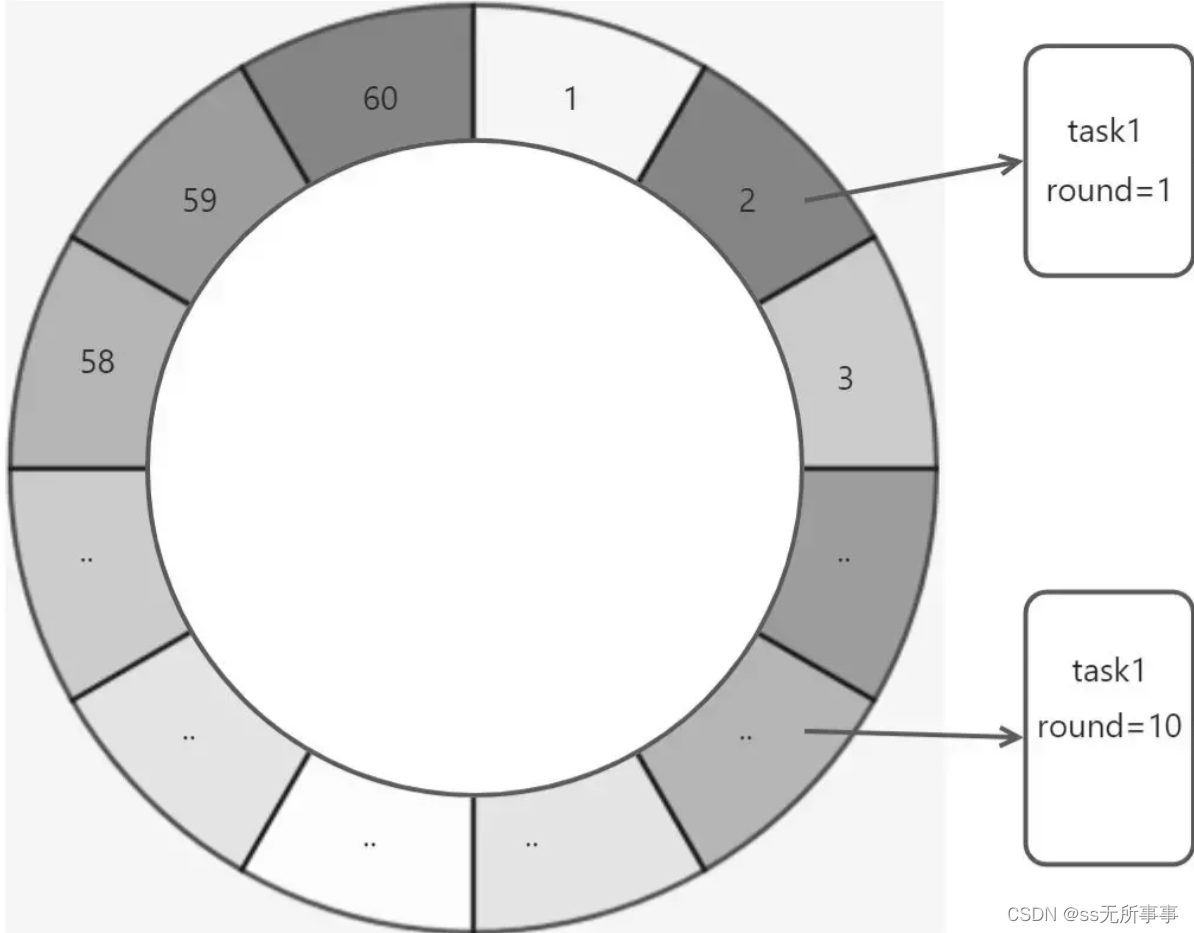
每个数组下标代表一个时间单位,例如小时或秒,而下标中存储的是在该时间单位内需要执行的任务。通过不断地轮转时间轮,将任务按照时间的先后顺序放入对应的槽位中。当时间轮转到某个槽位时,就执行该槽位上的所有任务
我在网上找了找了一张时间轮的图片(这看一眼应该就理解了)