🍉博客主页:阿博历练记
📖文章专栏:数据结构与算法
🚍代码仓库:阿博编程日记
🍡欢迎关注:欢迎友友们点赞收藏+关注哦🌹

文章目录
- 🎄链式二叉树
- 🔍1.二叉树的框架
- 🔍2.二叉树的创建
- 🔍3.二叉树的遍历
- 🃏遍历访问二叉树的时间复杂度和空间复杂度
- 🔍4.二叉树结点个数
- 🎯遍历计数法的误区
- 🧾static的作用
- 🔍5.二叉树叶子结点个数
- 🔍6.二叉树的高度
- ❌<font color=red size=4>误区(没有记录结果)
- ✔代码改进
- 💭思考:误区写法消耗是否是改进写法的2倍
- 🔍7.二叉树第k层结点个数
- 🔍8.二叉树查找值为x的结点
- 🔥误区写法1
- 🔥误区写法2
- 🔍9.二叉树的层序遍历
- 📢误区解析
- 🔍10.二叉树的销毁
- 🔍11.判断二叉树是否是完全二叉树
- 🧸test.c
- 🧸Queue.c
- 🧸Queue.h
🎄链式二叉树
🔍1.二叉树的框架
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
🔍2.二叉树的创建
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
BTNode* CreateBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
🔍3.二叉树的遍历
友友们,二叉树的遍历分为三种:前序遍历,中序遍历,后序遍历.
前序遍历:根结点------左子树------右子树.(从左向右)
中序遍历:左子树------根结点------右子树.(从左向右)
后序遍历:左子树------右子树------根结点.(从左向右)
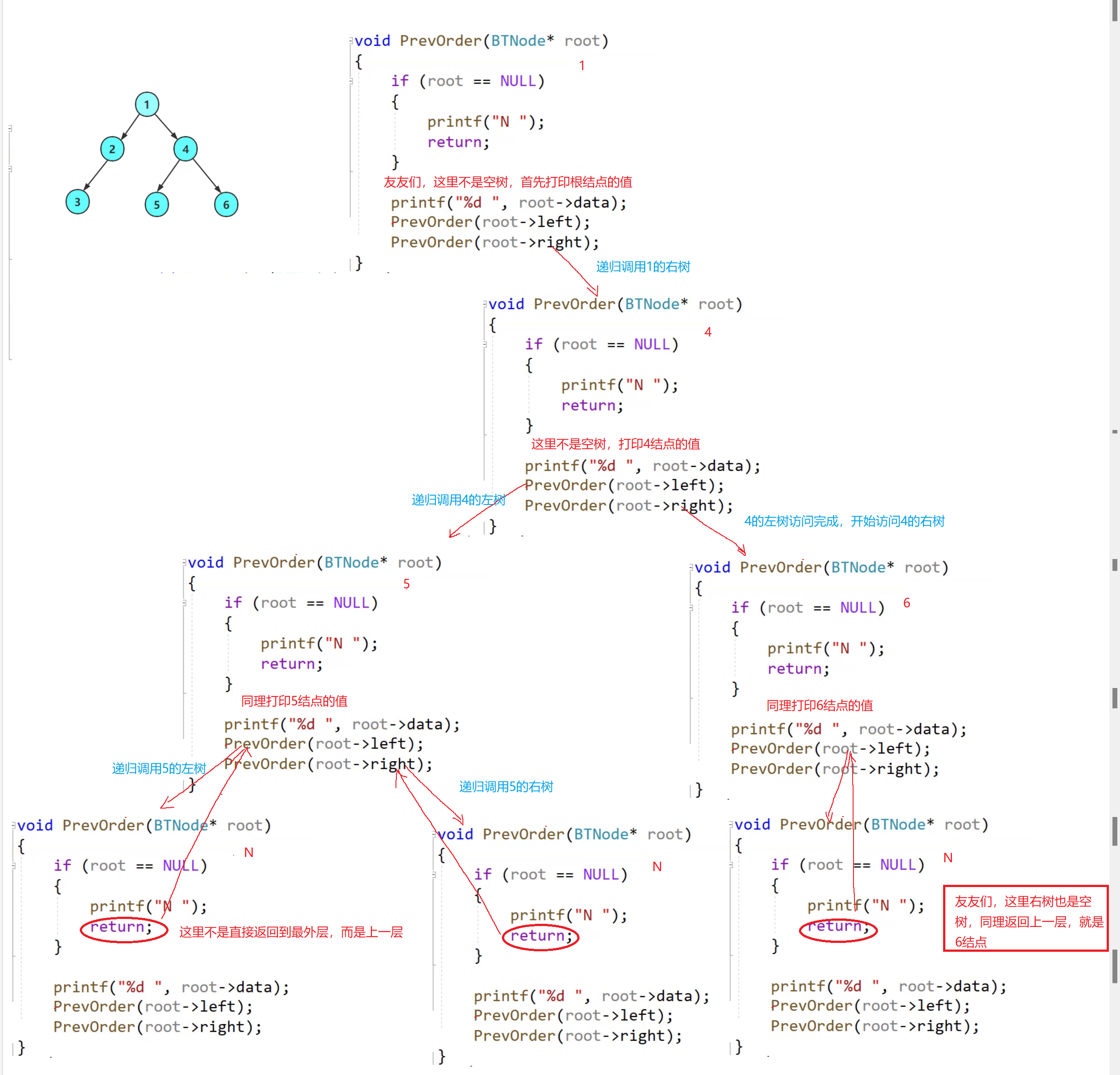
🤡1.前序遍历
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
🧠递归图理解分析
⚡递归调用左子树
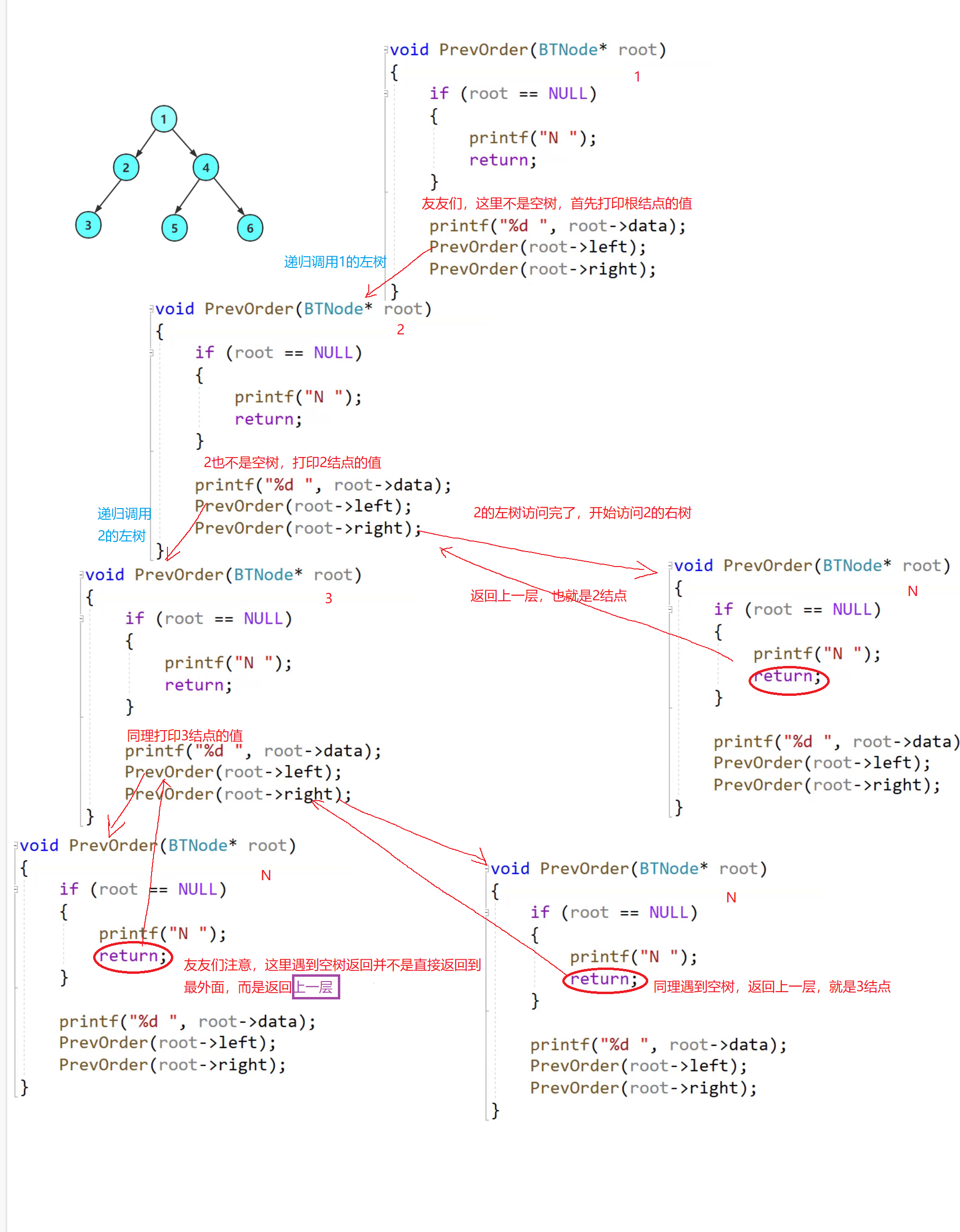
⚡递归调用右子树
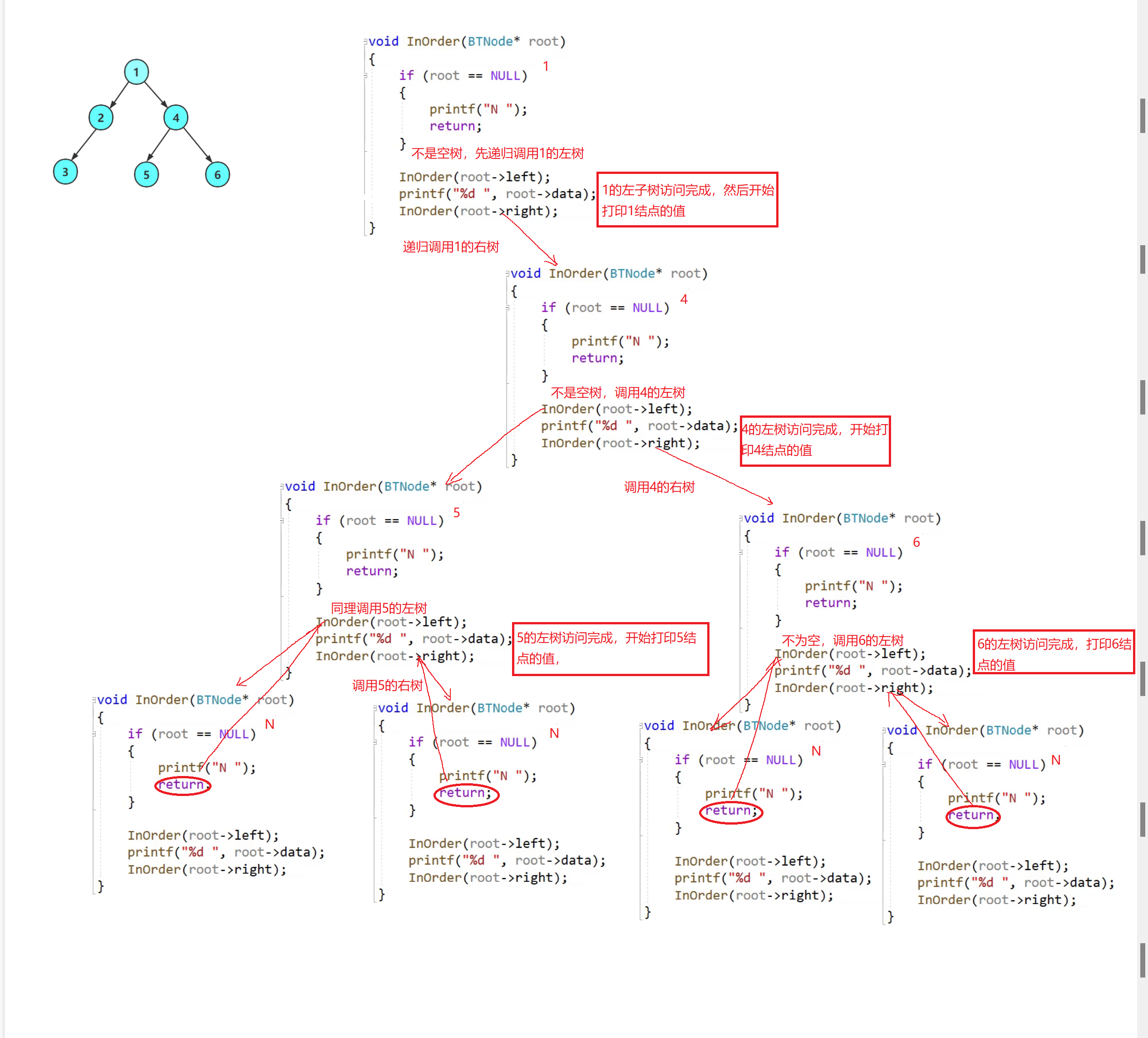
🤡2.中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
🧠递归图理解分析
⚡递归调用左子树
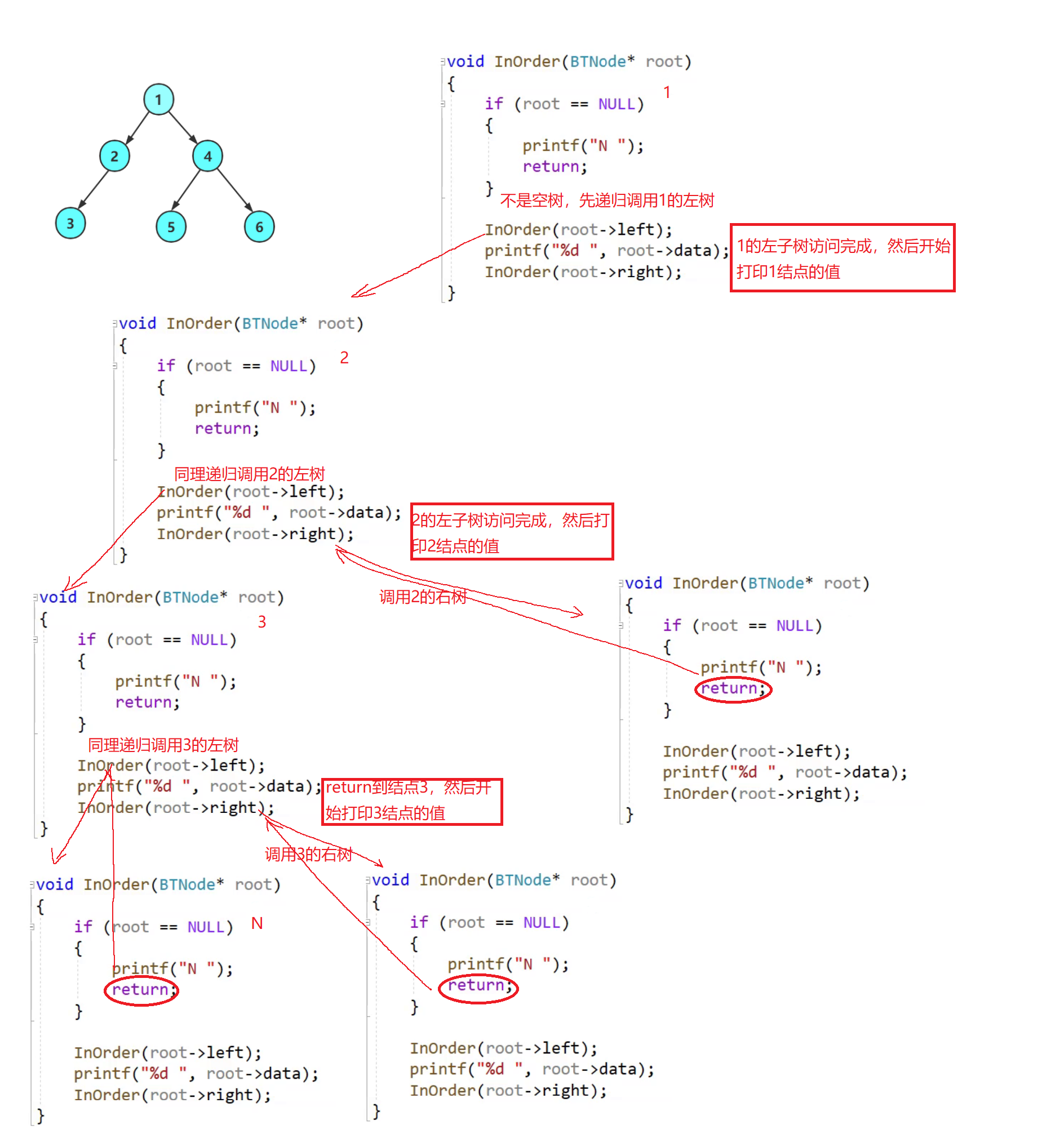
⚡递归调用右子树
🤡3.后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
⭐⭐友友们,这里我们可以看出来,其实先序,中序,后序遍历的差别就是访问根结点值的先后顺序不同.
🃏遍历访问二叉树的时间复杂度和空间复杂度
💫时间复杂度:友友们,这里我们需要思考n个结点在递归调用的时候需要建立多少个栈帧呢,很显然除了空结点,每一个结点都会建立两个栈帧去访问它的左子树和右子树,所以会有2n个函数栈帧,但是量级还在N上,所以时间复杂度是O(N).
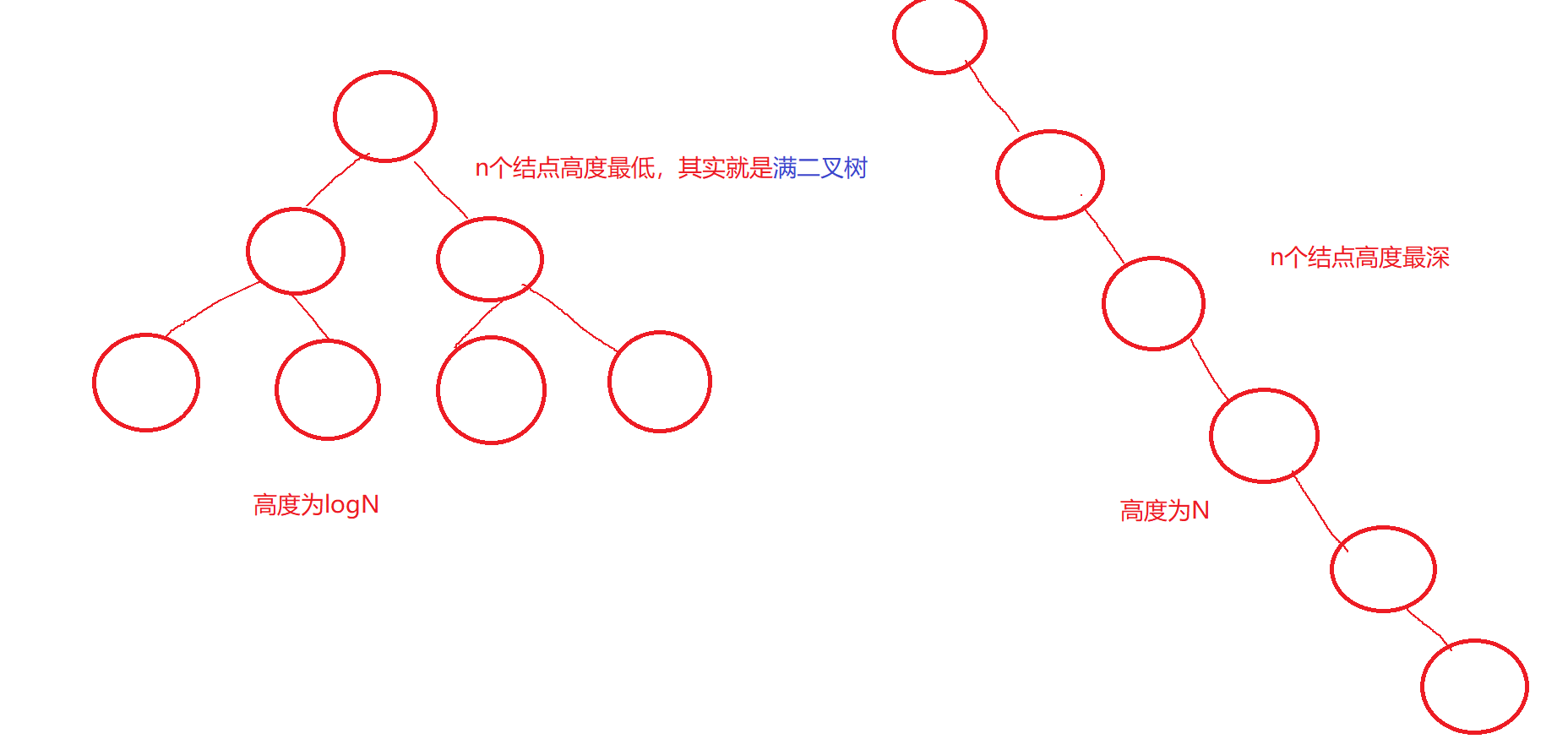
💫空间复杂度:O(h),h是二叉树的高度,h的范围在
logN~N之间,
时间是累加计算的,空间可以重复利用,左子树调用函数建立栈帧,当往上一层返的时候,左子树建立的栈帧销毁,右子树建立栈帧,这里其实左子树和右子树建立的栈帧是同一个,所以我们的空间复杂度是看树的深度.
🔍4.二叉树结点个数
✨1.递归法
int BTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BTreeSize(root->left) + BTreeSize(root->right) + 1;
}
🧠递归图理解分析
⚡递归调用左子树
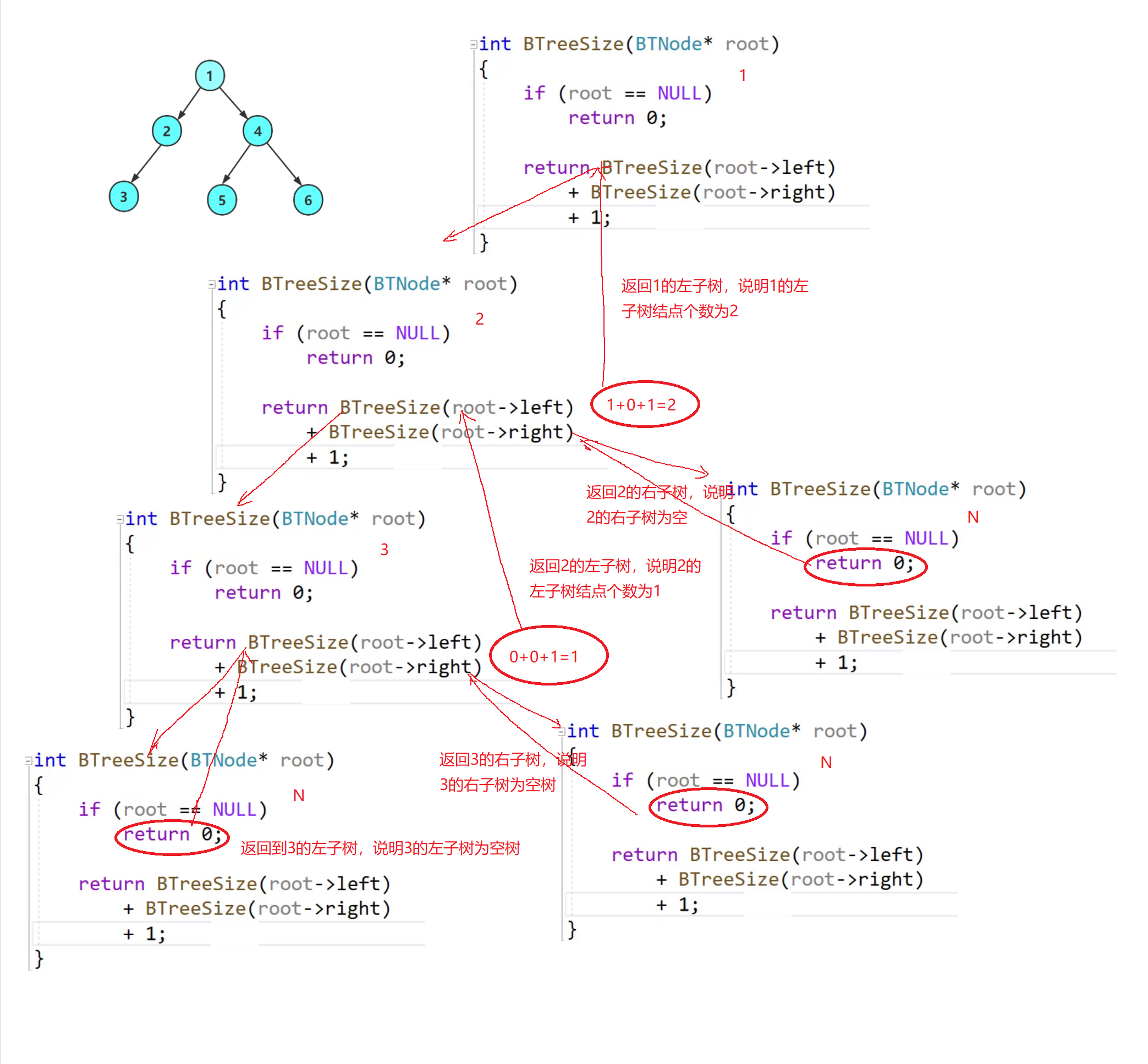
⚡递归调用右子树
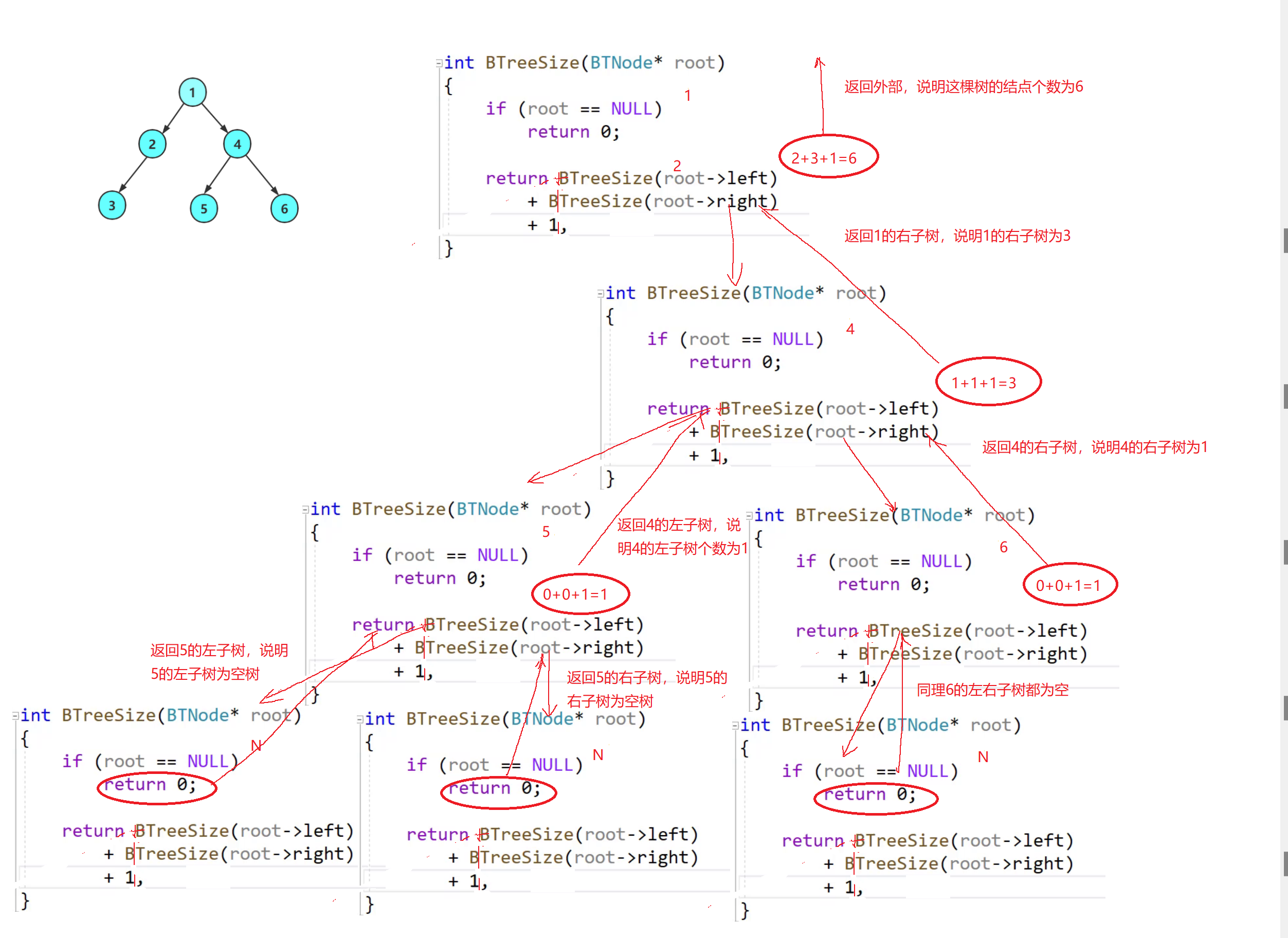
✨2.遍历计数法
int size = 0;
void BTreeSize(BTNode* root)
{
if (root == NULL)
return ;
size++;
BTreeSize(root->left);
BTreeSize(root->right);
}
🎯遍历计数法的误区
❌误区1
void BTreeSize(BTNode* root)
{
int size = 0;
if (root == NULL)
return;
size++;
BTreeSize(root->left);
BTreeSize(root->right);
}
友友们,这里需要注意了,因为我们这个size是在函数内部定义的,然后递归调用的时候,每个函数栈帧里面都会重新定义一个size,这样就不会让size达到累加的效果.
❌误区2
void BTreeSize(BTNode* root)
{
static int size = 0;
if (root == NULL)
return;
size++;
BTreeSize(root->left);
BTreeSize(root->right);
}
🧾static的作用
1.static修饰局部变量:
static修饰局部变量时,使得被修饰的变量成为静态变量,存储在静态区。存储在静态区的数据生命周期与程序相同,在main函数之前初始化,在程序退出时销毁。(无论是局部静态还是全局静态),但并没有改变局部变量的作用域.
2.static修饰全局变量:
全局变量本来就存储在静态区,因此static并不能改变其存储位置。但是,static限制了其链接属性。被static修饰的全局变量只能被该包含该定义的文件访问.(即改变了作用域)
3.static修饰函数:
static修饰函数使得函数只能在包含该函数定义的文件中被调用。对于静态函数,声明和定义需要放在同一个文件夹中.
所以友友们,这里static int size=0这句代码只在第一次进行了初始化,之后编译器会跳过这句代码执行下一句.所以这里的size可以求出树结点的个数,但是size变成了一个静态局部变量,作用域仍然是这个函数,我们在外面是无法访问的.
❌误区3(return size的个数)
int BTreeSize(BTNode* root)
{
static int size = 0;
if (root == NULL)
return size;
size++;
BTreeSize(root->left);
BTreeSize(root->right);
return size;
}
友友们,这种情况虽然只有第一次调用才能取出正确的size,因为当我们进行多次调用的时候,那个size会在第一次调用的基础上再次计算size,它不是从0开始的,我们也没有办法在外面把size置0,因为它变成了一个静态局部变量,它仍然只作用于这个函数.
✔正确样例
int size = 0;
void BTreeSize(BTNode* root)
{
if (root == NULL)
return ;
size++;
BTreeSize(root->left);
BTreeSize(root->right);
}
友友们,这样就可以了,我们把size定义为一个全局变量,但是需要注意的是当重复调用该函数时,我们需要提前把size置0.
🔍5.二叉树叶子结点个数
int BTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}
🧠递归图理解分析
⚡递归调用左子树
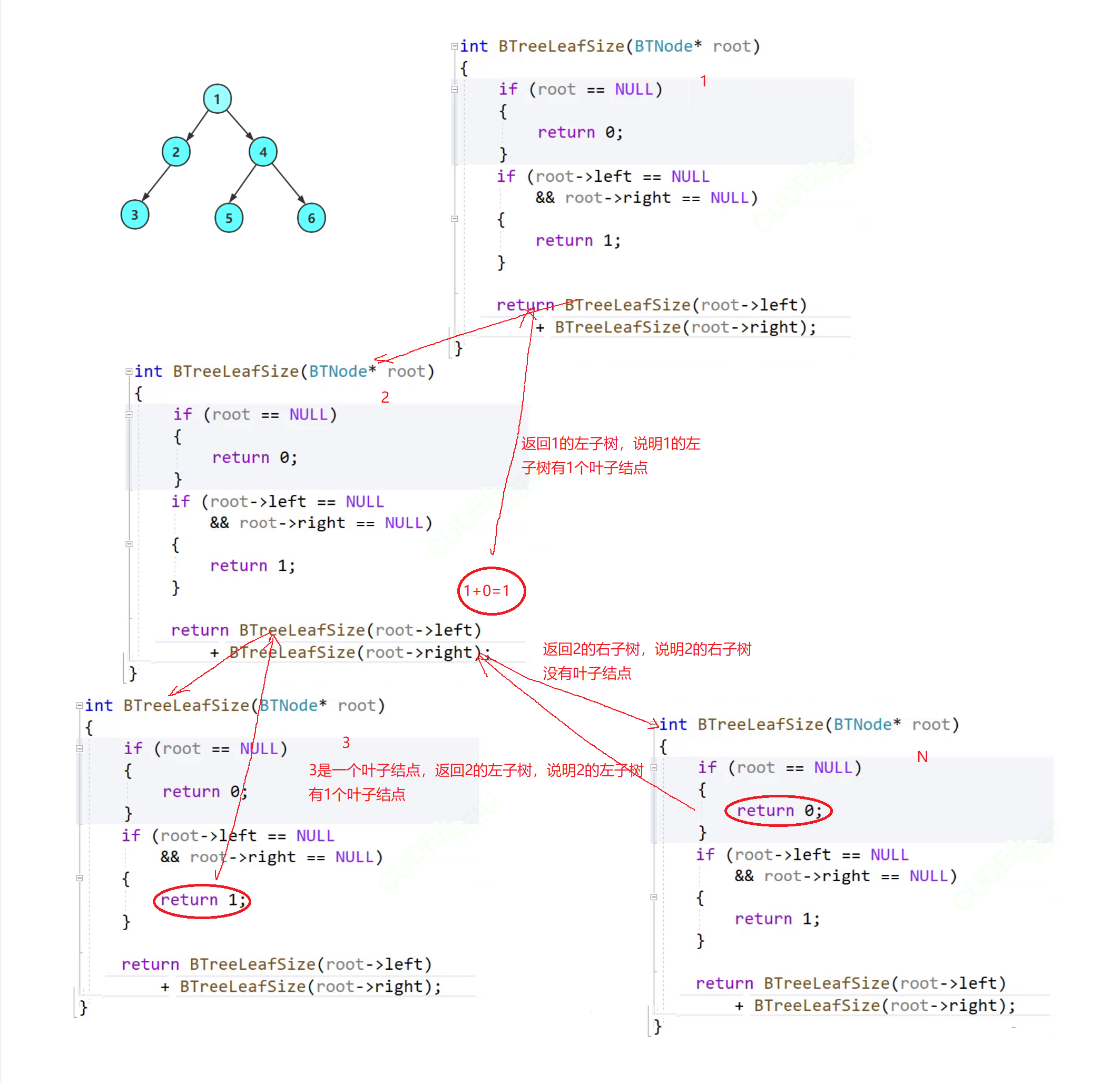
⚡递归调用右子树
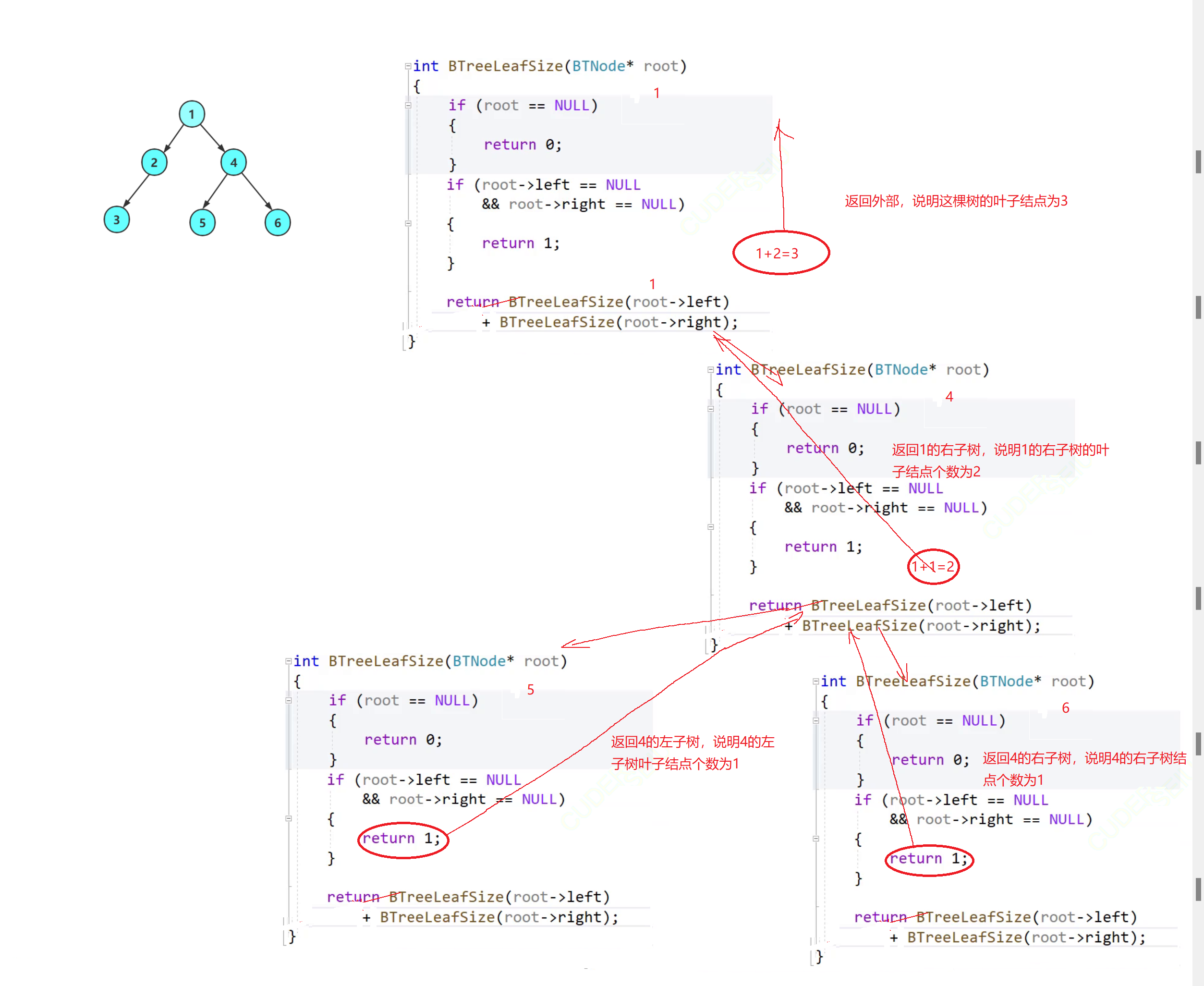
🔍6.二叉树的高度
❌误区(没有记录结果)
int BTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BTreeHeight(root->left)> BTreeHeight(root->right)?BTreeHeight(root->left)+1 : BTreeHeight(root->right)+ 1;
}
✔代码改进
int BTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int LeftHeight = BTreeHeight(root->left);
int RightHight = BTreeHeight(root->right);
return LeftHeight > RightHight ? LeftHeight + 1 : RightHight + 1;
}
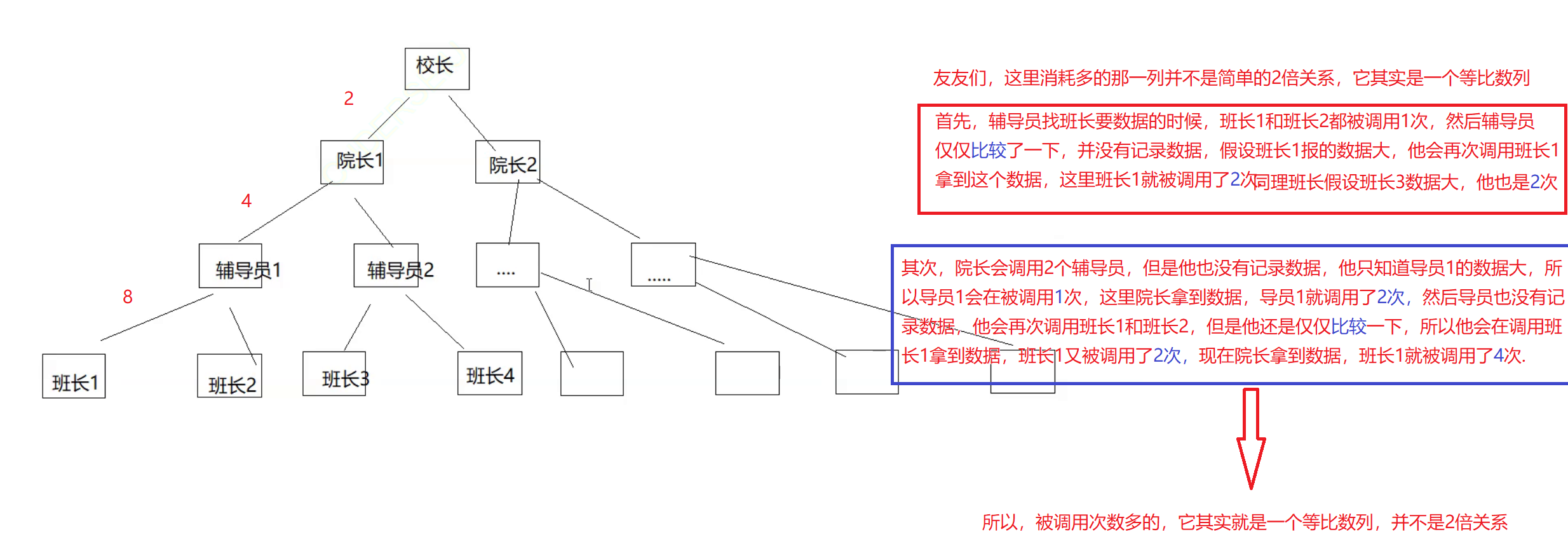
💭思考:误区写法消耗是否是改进写法的2倍
并不是2倍的关系,误区写法要比改进写法慢很多!
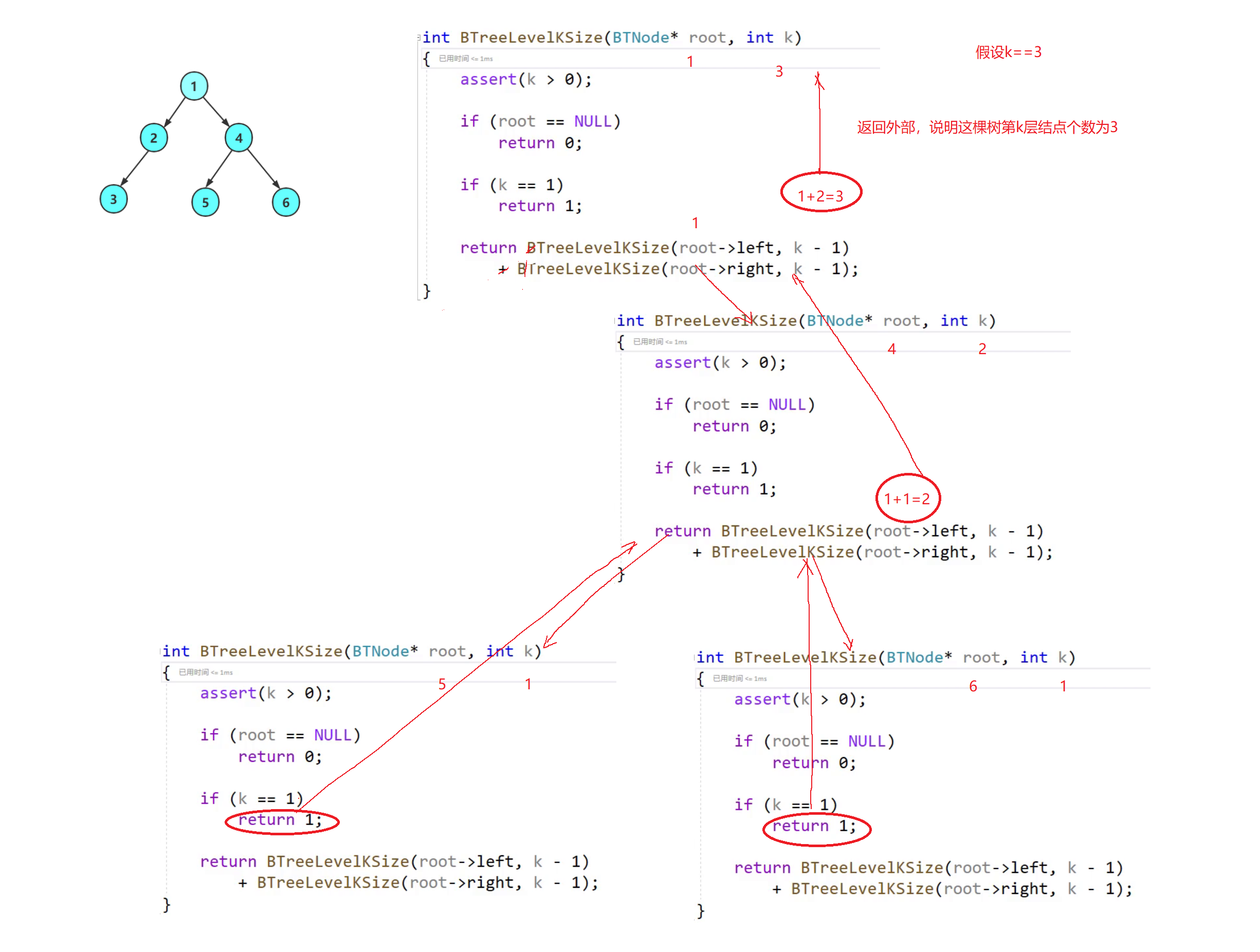
🔍7.二叉树第k层结点个数
int BTreeLevelKSize(BTNode* root, int k)
{
assert(k>0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BTreeLevelKSize(root->left, k - 1) + BTreeLevelKSize(root->right, k - 1);
}
友友们,这里我们可以把它转化为子问题:求左子树的第k-1层和右子树的第k-1层.结束条件:❤1.k==1且结点不为空 ❤2.结点为空.
🧠递归图理解分析
⚡递归调用左子树
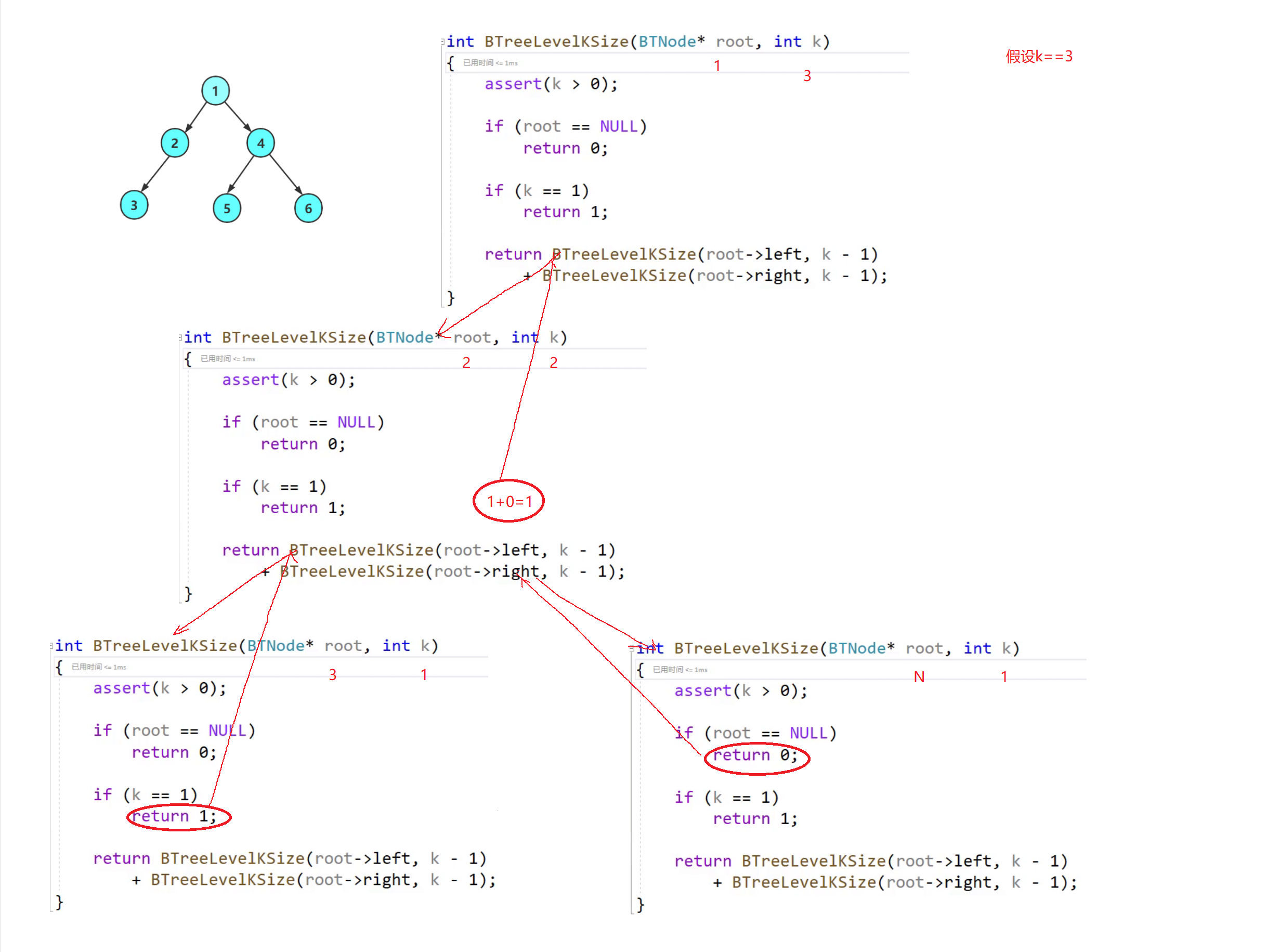
⚡递归调用右子树
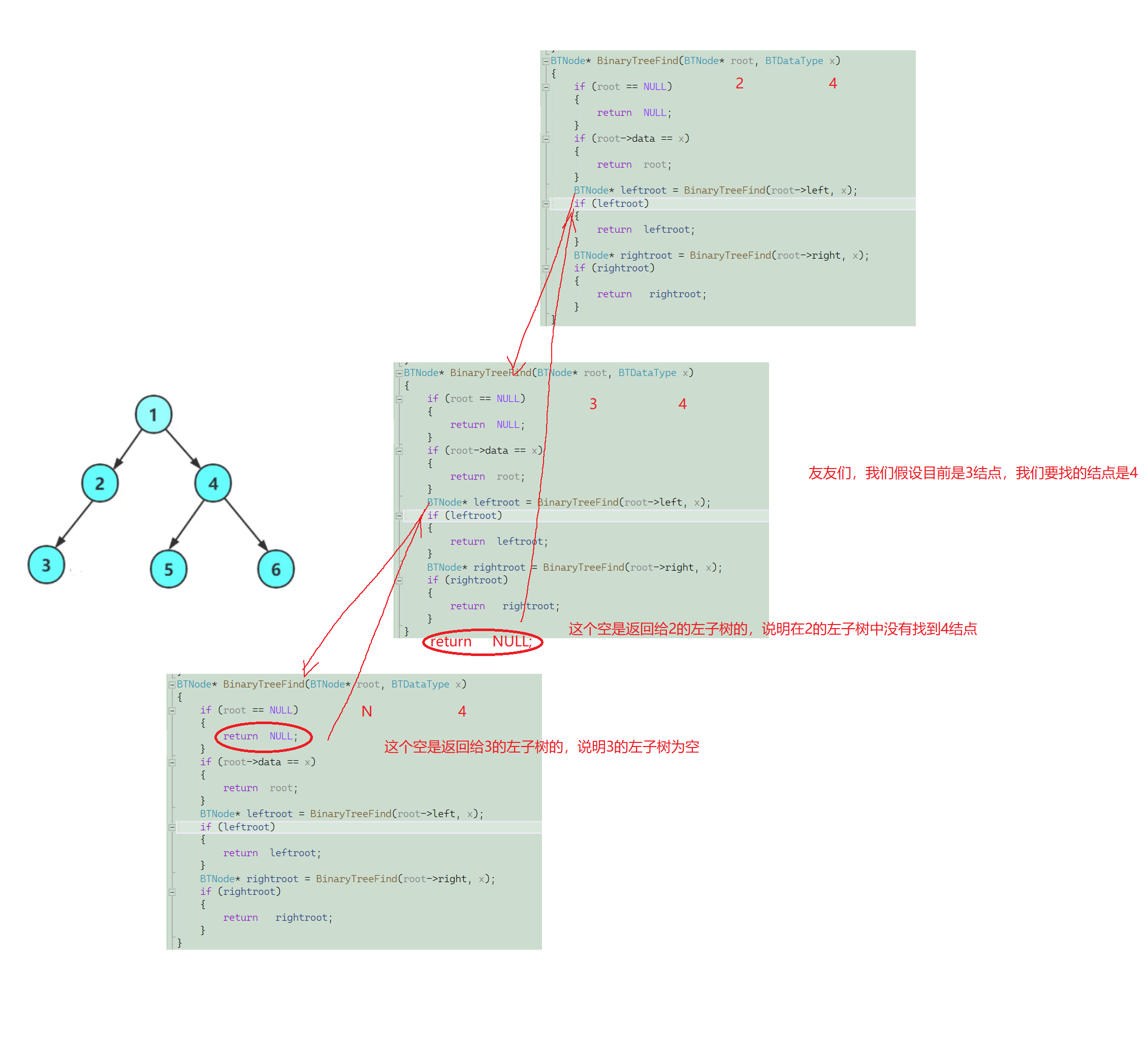
🔍8.二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* leftroot = BinaryTreeFind(root->left, x);
if (leftroot)
{
return leftroot;
}
BTNode* rightroot = BinaryTreeFind(root->right, x);
if (rightroot)
{
return rightroot;
}
return NULL;
}
🧠递归图理解分析
⚡递归调用左子树
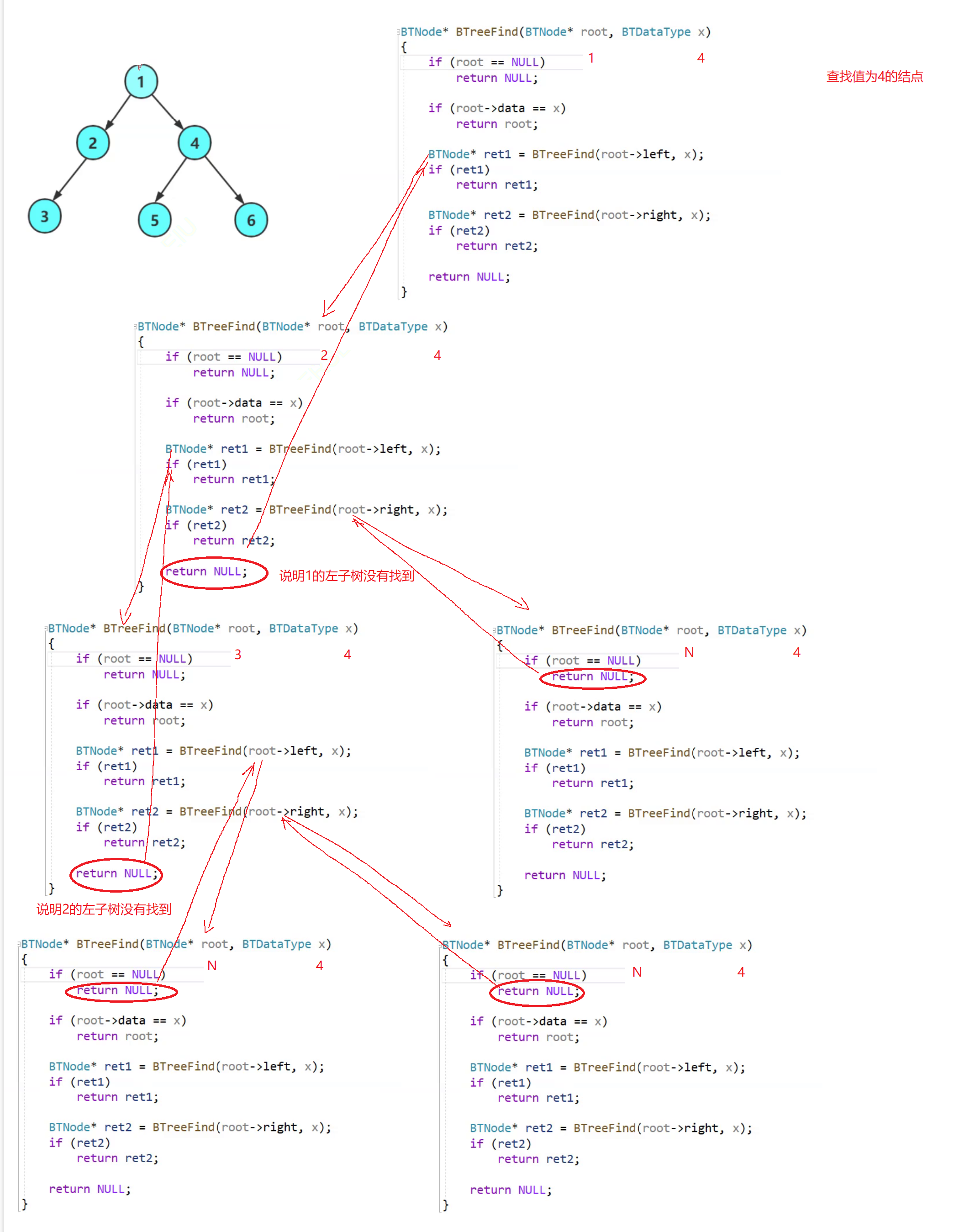
⚡递归调用右子树

🔥误区写法1
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BinaryTreeFind(root->left, x);
BinaryTreeFind(root->right, x);
}
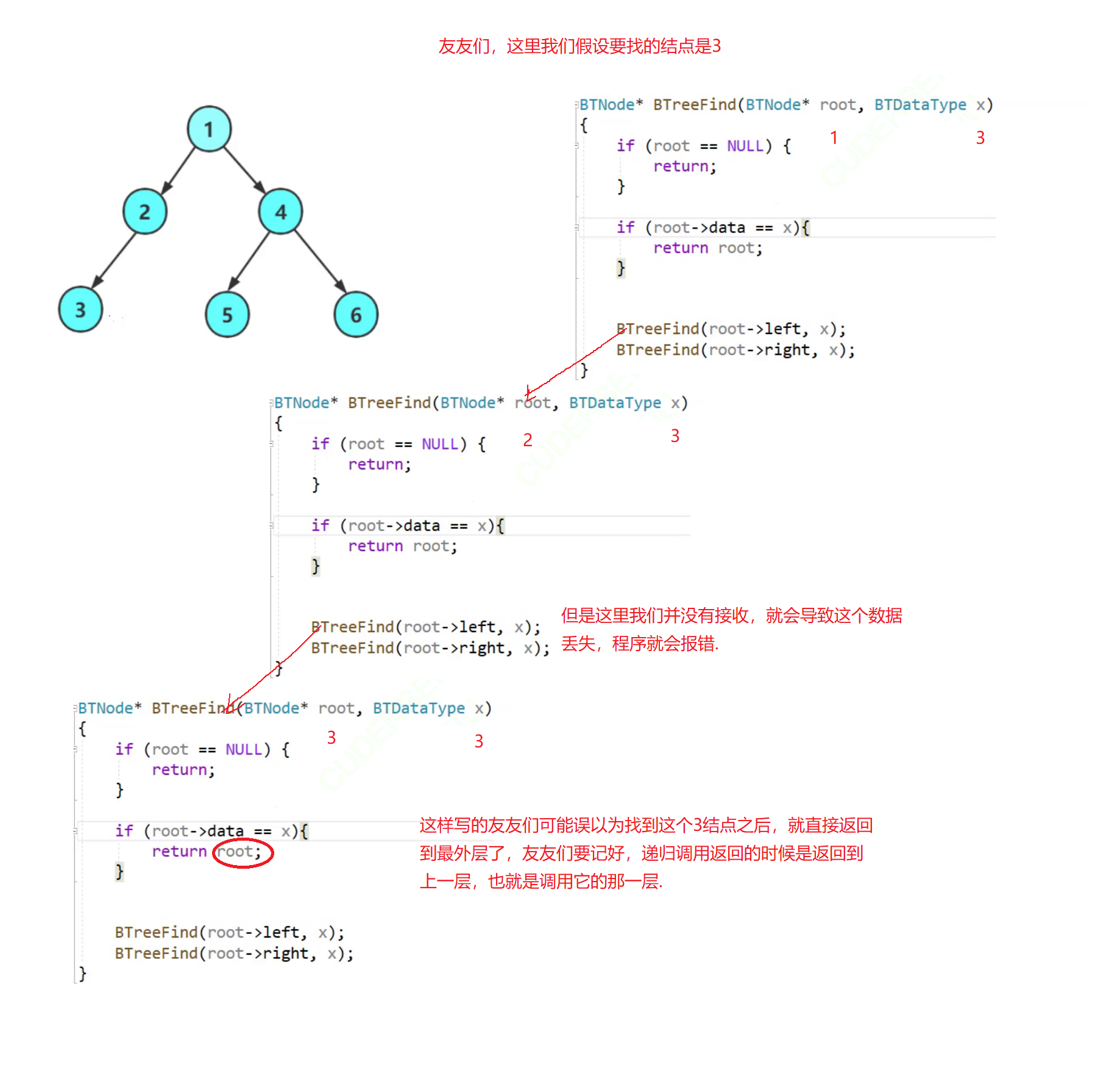
🔥误区写法2
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* leftroot = BinaryTreeFind(root->left, x);
if (leftroot)
{
return leftroot;
}
BTNode* rightroot = BinaryTreeFind(root->right, x);
if (rightroot)
{
return rightroot;
}
}
友友们,这种写法就是当这个结点和它的左子树以及右子树都不是要找的结点的时候没有返回值,可能友友们会误以为没有找到的话,第一个if语句不就体现出来了吗,这里不是这样的,我们可以举个例子。
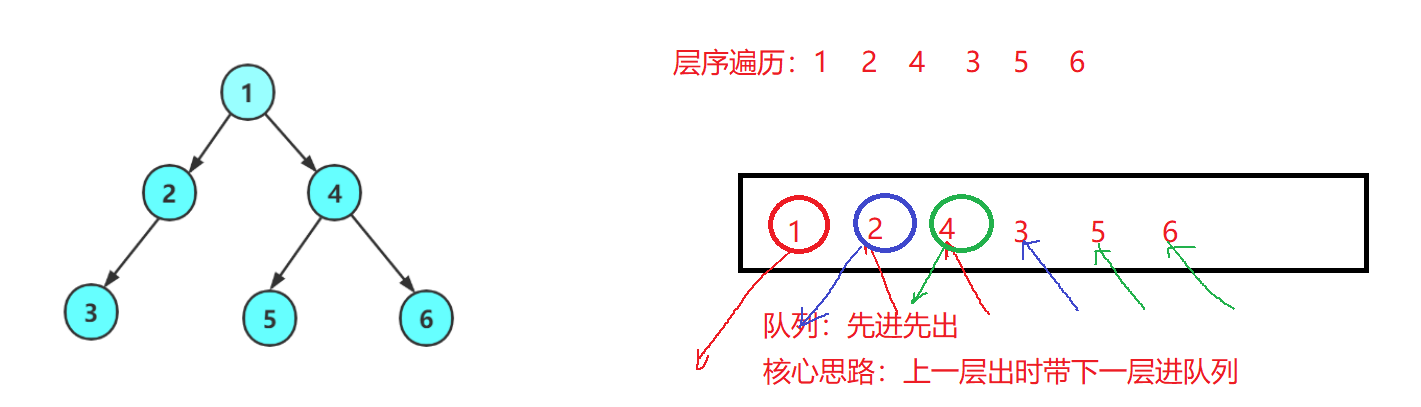
🔍9.二叉树的层序遍历
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root == NULL)
{
return;
}
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
//printf("%d ", front->data);
QueuePop(&q);
printf("%d ", front->data);
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
printf("\n");
QueueDestroy(&q);
}
📢误区解析
🎲1.友友们,这里我们的操作是改变QDataType的类型,把它改变为树结点的指针,这样我们就可以访问树的左子树和右子树了.
🎲2.友友们可能会想Queuepop之后,front不就成为野指针了吗,我们再去打印front->data这不就是对空指针的解引用吗,这里是这样的,front不是队列结点的指针,它是树结点的指针,而我们pop的是队列结点的指针,所以不影响我们树结点指针的使用.
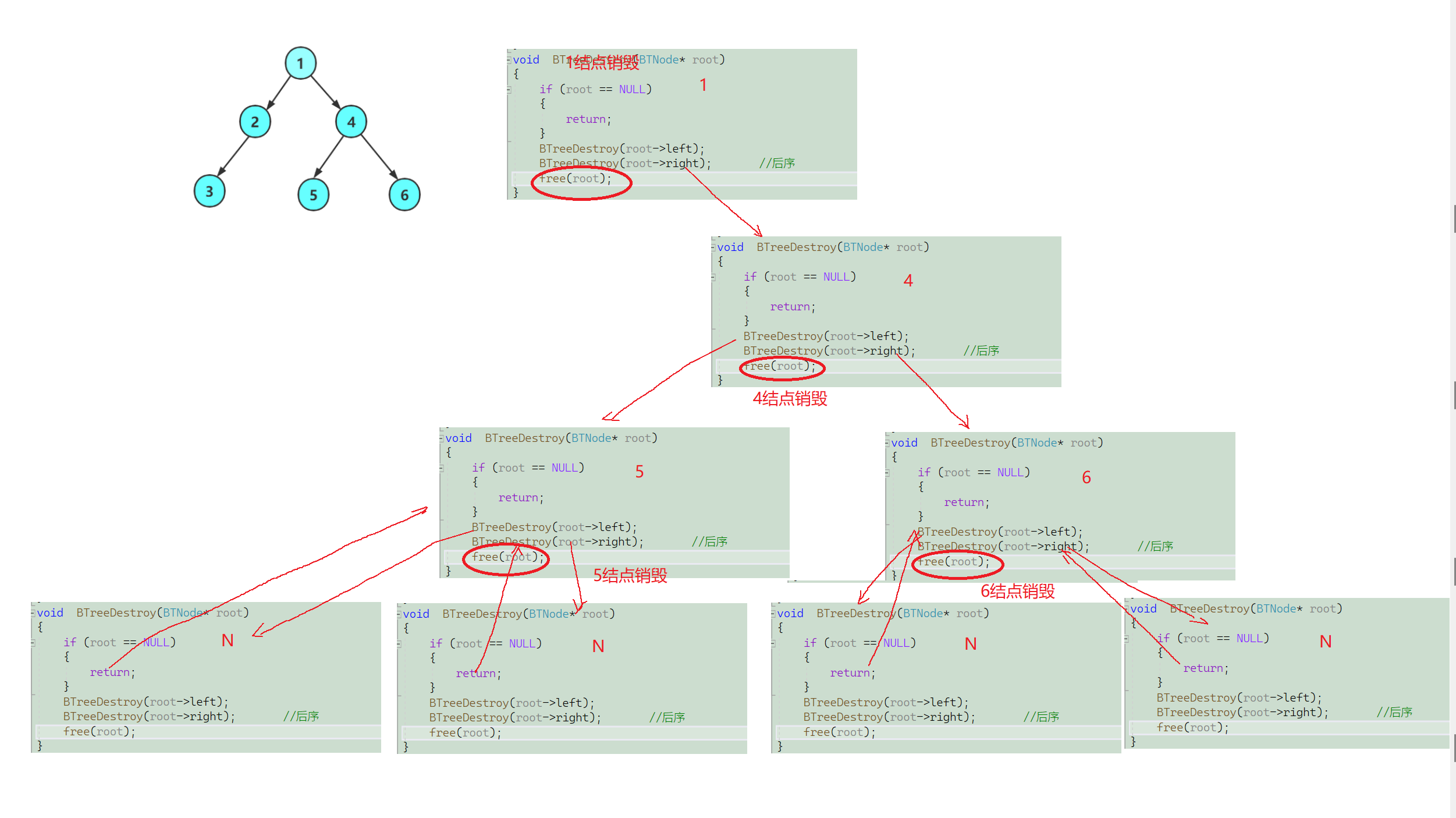
🔍10.二叉树的销毁
1.前序销毁
void BTreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
BTNode* Left = root->left;
BTNode* Right = root->right;
free(root); //先序
BTreeDestroy(Left);
BTreeDestroy(Right);
}
友友们这里要注意的是,我们如果采用前序的话,我们必须先保存它的左右子树,否则我们销毁根节点之后,我们就无法访问到它的左右子树了,这里推荐采用后序进行销毁.
2.后序销毁
void BTreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
BTreeDestroy(root->left);
BTreeDestroy(root->right); //后序
free(root);
}
🧠递归图理解分析
⚡递归调用左子树
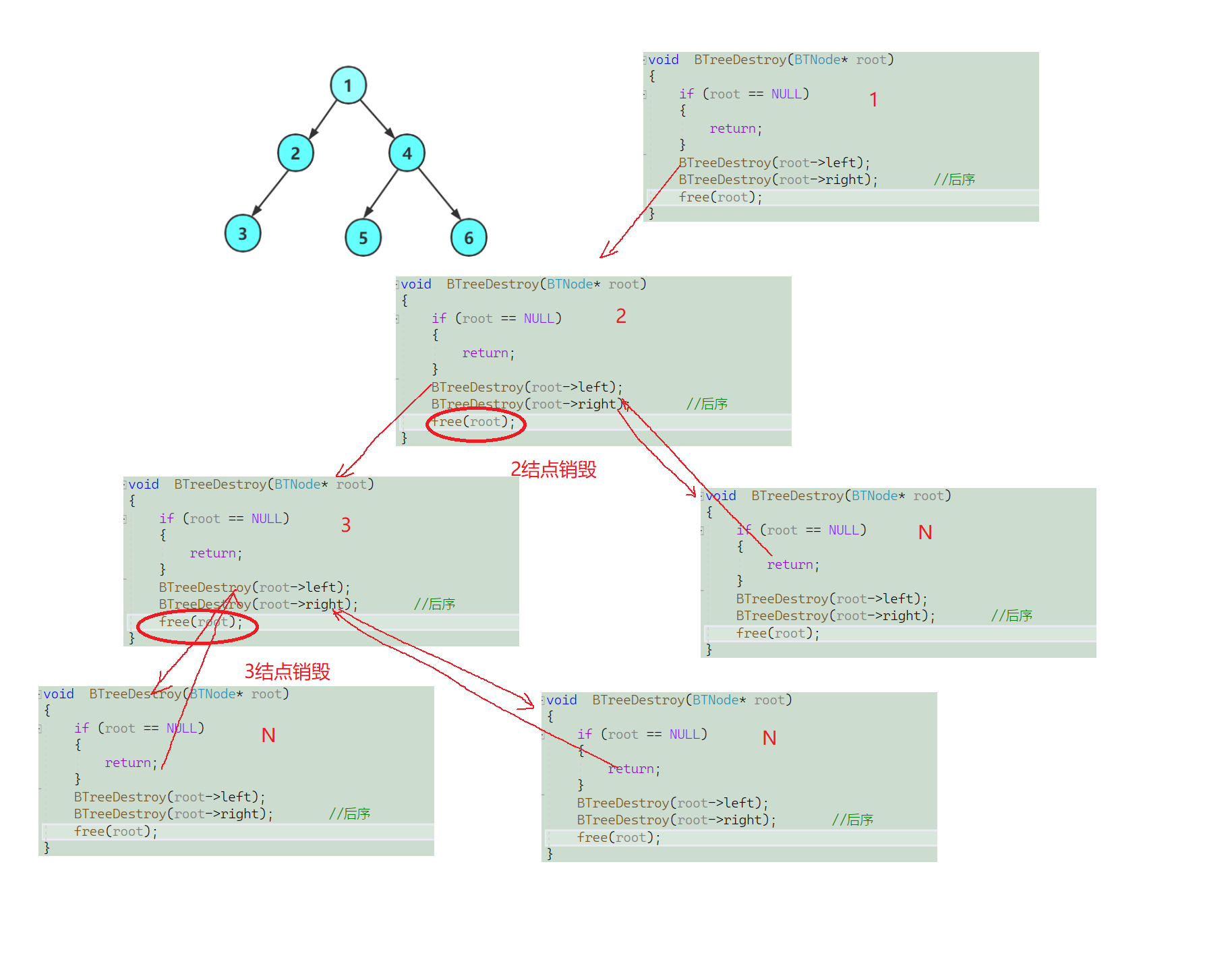
⚡递归调用右子树
🔍11.判断二叉树是否是完全二叉树
bool BTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root == NULL)
return true;
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
//遇到空树就跳出循环
if (front == NULL)
{
break;
}
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
//检查后面的结点有没有非空,如果有非空,就不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}

🧸test.c
#define _CRT_SECURE_NO_WARNINGS 1
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdlib.h>
#include<assert.h>
#include<stdio.h>
#include"tree.h"
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
BTNode* CreateBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
//二叉树的前序遍历
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
//二叉树的中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
//二叉树的后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
//二叉树结点个数
int BTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BTreeSize(root->left) + BTreeSize(root->right) + 1;
}
//int size = 0;
//void BTreeSize(BTNode* root)
//{
// if (root == NULL)
// return ;
// size++;
// BTreeSize(root->left);
// BTreeSize(root->right);
//}
// 二叉树叶子节点个数
int BTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}
//求二叉树的高度
int BTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int LeftHeight = BTreeHeight(root->left);
int RightHight = BTreeHeight(root->right);
return LeftHeight > RightHight ? LeftHeight + 1 : RightHight + 1;
}
// 二叉树第k层节点个数
int BTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BTreeLevelKSize(root->left, k - 1) + BTreeLevelKSize(root->right, k - 1);
}
//二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* leftroot = BinaryTreeFind(root->left, x);
if (leftroot)
{
return leftroot;
}
BTNode* rightroot = BinaryTreeFind(root->right, x);
if (rightroot)
{
return rightroot;
}
return NULL;
}
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* leftroot = BinaryTreeFind(root->left, x);
if (leftroot)
{
return leftroot;
}
BTNode* rightroot = BinaryTreeFind(root->right, x);
if (rightroot)
{
return rightroot;
}
}
//二叉树的层序遍历
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root == NULL)
{
return;
}
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
//printf("%d ", front->data);
QueuePop(&q);
printf("%d ", front->data);
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
printf("\n");
QueueDestroy(&q);
}
void BTreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
BTreeDestroy(root->left);
BTreeDestroy(root->right); //后序
free(root);
}
//判断二叉树是否是完全二叉树
bool BTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root == NULL)
return true;
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
//遇到空树就跳出循环
if (front == NULL)
{
break;
}
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
//检查后面的结点有没有非空,如果有非空,就不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
int main()
{
BTNode* root = CreateBinaryTree();
PrevOrder(root);
printf("\n");
InOrder(root);
printf("\n");
PostOrder(root);
printf("\n");
printf("BTreeSize:%d\n", BTreeSize(root));
printf("BTreeeafSize:%d\n", BTreeLeafSize(root));
printf("BTreeHeight:%d\n", BTreeHeight(root));
printf("BTreeLevelKSize:%d\n", BTreeLevelKSize(root, 4));
printf("BTreeComplete:%d\n", BTreeComplete(root));
LevelOrder(root);
BTreeDestroy(root);
root = NULL;
return 0;
}
🧸Queue.c
#define _CRT_SECURE_NO_WARNINGS 1
#define _CRT_SECURE_NO_WARNINGS 1
#include"tree.h"
void QueueInit(Queue* pq)
{
assert(pq);
pq->phead = pq->ptail = NULL;
pq->size = 0;
}
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->phead;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
/*QNode* del = cur;
cur = cur->next;
free(del);*/
}
pq->phead = pq->ptail = NULL;
pq->size = 0;
}
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail");
return;
}
newnode->data = x;
newnode->next = NULL;
if (pq->phead == NULL)
{
assert(pq->ptail == NULL);
pq->phead = pq->ptail = newnode;
}
else
{
pq->ptail->next = newnode;
pq->ptail = newnode;
}
pq->size++;
}
void QueuePop(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
//1个结点
if (pq->phead->next == NULL)
{
free(pq->phead);
pq->phead = pq->ptail = NULL; //不能对同一动态开辟出来的空间进行多次free释放,这里我们释放完pq->phead之后,pq->ptail也已经被释放了,所以我们主要的目的就是把pq->phead和pq->ptail都置空
}
//多个结点
else
{
QNode* next = pq->phead->next;
free(pq->phead);
pq->phead = next;
}
pq->size--;
}
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->phead->data;
}
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->ptail->data;
}
int QueueSize(Queue* pq)
{
assert(pq);
return pq->size;
}
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->phead == NULL
&& pq->ptail == NULL;
}
🧸Queue.h
#pragma once
#pragma once
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{
QDataType data;
struct QueueNode* next;
}QNode;
typedef struct Queue
{
QNode* phead;
QNode* ptail;
int size;
}Queue;
void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);