题目描述

FJ gave Bessie an array aa of length $N(2\le N\le 500,-10^{15}\le ai\le 10^{15})$ with all $\frac{N(N+1)}{2}$​ contiguous subarray sums distinct. For each index $i\in [1,N]$, help Bessie compute the minimum amount it suffices to change ai by so that there are two different contiguous subarrays of a with equal sum.

翻译

给定长度为 $N$ 的数组 $a$（$2\le N\le 500,-10^{15}\le ai\le 10^{15}$），$a$ 中所有 $\frac{N(N+1)}{2}$​ 个连续子段和互不相等。对于每个 $i\in [1,N]$，把 $a_i$ 修改成一个值，使得存在两个不同的连续子段，它们的和相等，且改值与 $a_i$ 的差最小，求出这个差。

题解

发现 $N\le 500$，大胆猜测时间复杂度 $O(N^3)$

对于每个连续子段 $[l,r]$，将它的左右端点与子段和保存，按照子段和从小到大的顺序排序。预处理的时间复杂度是 $O(N^2\log N)$ 的。

回答询问时，对于 $i$，把所有包含 $i$ 的连续子段标记。

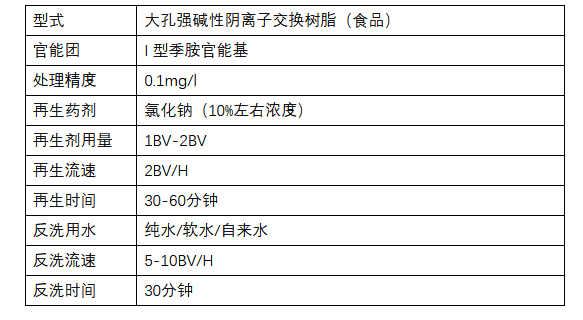
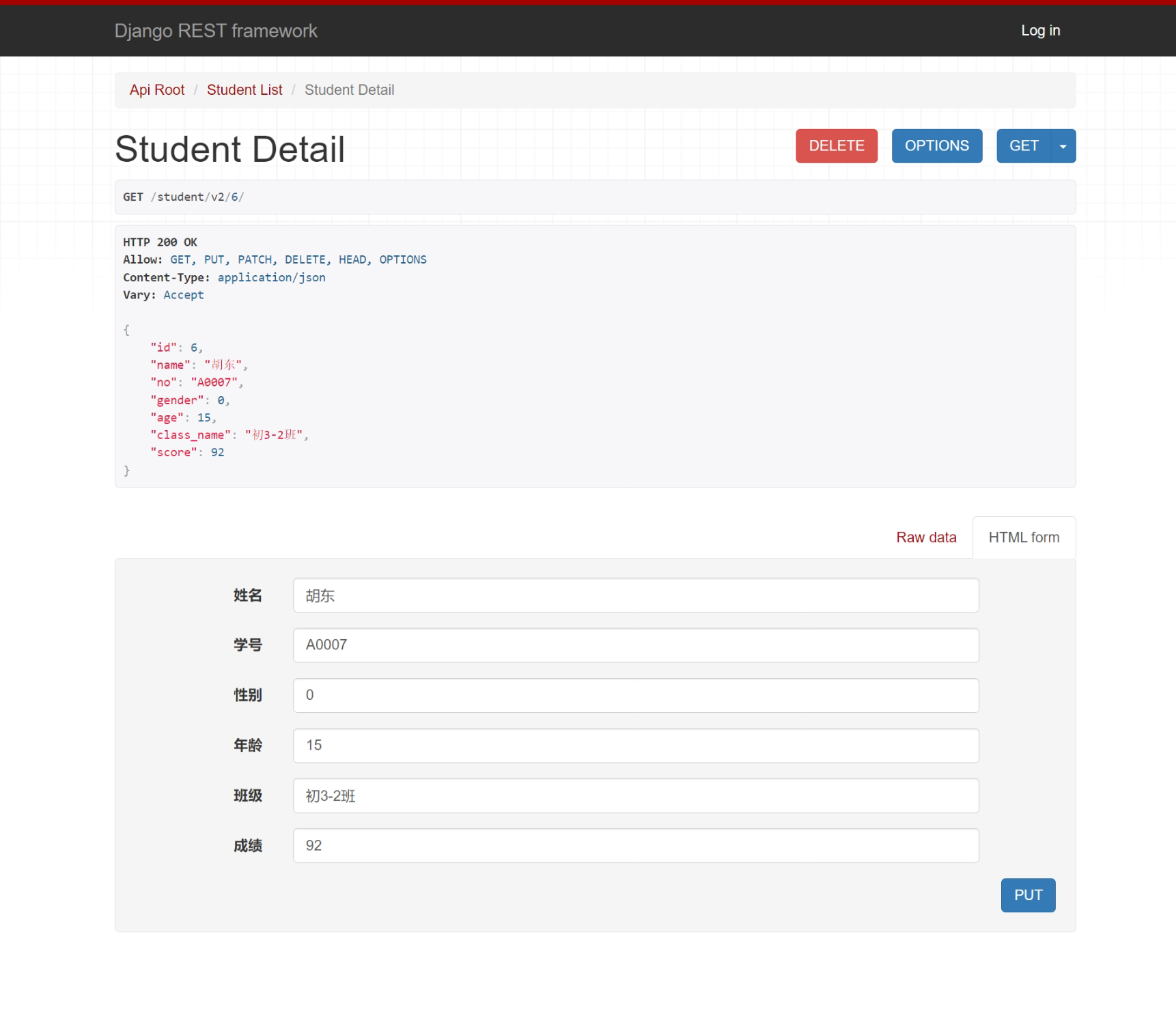
下面画图帮助理解。

上面的表格表示 $sum$ 的大小，红色表示被标记的子段和所在的位置，蓝色是未标记的。

题目中把 $a_i$ 修改，其实等价于在这个表格中把所有红色的位置整体平移；
若存在两个不同的连续子段，它们的和相等，就是平移后存在某个红色的位置与原先一个蓝色的位置重合。
使二者重合的平移量是多少呢？即为相邻两个颜色不同的位置距离最小值。

于是只要用 $O(N^2)$ 的时间标记和求最小值。

总的时间复杂度为 $O(N^3)$。

下为赛时代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=501;
int n,cnt,bj[(N-1)*N/2+1];
ll a[N],sum[N],b[N][N];
struct node
{
    int l,r;
    ll sum;
    node(){}
    node(int x,int y,ll z){l=x,r=y,sum=z;}
    bool operator<(const node &a)const{
        return sum<a.sum;
    }
}czn[(N-1)*N/2+1];
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]),sum[i]=sum[i-1]+a[i];
    for(int i=1;i<=n;i++){
        for(int j=i;j<=n;j++){
            czn[++cnt]=node(i,j,sum[j]-sum[i-1]);
        }
    }
    sort(czn+1,czn+1+cnt);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=cnt;j++){
            if(czn[j].l<=i&&i<=czn[j].r){
                bj[j]=1;
            }
        }
        ll minn=1e18;
        for(int j=1;j<cnt;j++){
            if(bj[j]^bj[j+1]){
                minn=min(minn,abs(czn[j].sum-czn[j+1].sum));
            }
        }
        memset(bj,0,sizeof(bj));
        printf("%lld\n",minn);
    }
}