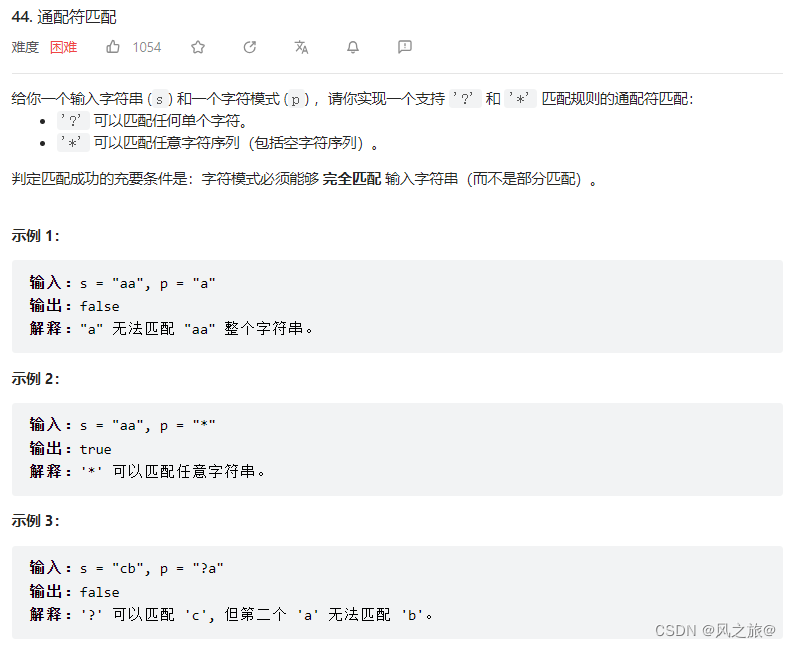
题目链接：力扣
所有的动态规划都可以使用暴力递归求解，如果推导dp方程比较困难，可以先使用暴力递归进行尝试，然后将从递归改为动态规划，这种方式在dp方程求解困难的情况下非常有效，而且从递归修改为动态规划时比较容易求解dp初始值以及dp的更新方式。
暴力递归解法：
- 题目是两个字符串匹配的过程，可以使用递归分解成子问题来做，递归求解的关键在于定义递归函数的含义，以及递归的终止条件
- 递归函数的定义：boolean process(char[] s,char[] p,int sL,int pL)：
- s：字符串s
- p：字符模式p
- sL：从字符串s的sL索引处开始匹配
- pL：从字符模式p的pL索引处开始匹配
- return：如果字符模式 p[pL，... ，N]完全匹配字符串s[sL，... ，M]，则返回true，否则返回false
- process递归函数的解释：判断字符模式p从索引pL开始一直到结束的的子串是否完全匹配字符串s从索引sL开始到结束的子串，如果完全匹配，返回true，否则，返回false
- 递归的终止条件：对于递归函数来说首先需要找到递归的结束条件
- 如果sL==s.length：这种情况下，字符串s已经完全被匹配完了(s的最后一个字符的索引为s.length-1)，但是字符模式p可能还有字符没有用完，需要分情况讨论
- pL==p.length：字符模式p的所有字符都用完了(字符模式p的最后一个字符的索引为p.length-1)，显然这种情况下，字符模式p完全匹配字符串s，递归函数返回true
- 否则：字符模式p还没有用完，但是这种情况下并不意味着正则表达式没有完全匹配字符串s，因为如果后面的字符全是*，可以让其匹配空字符消耗掉，这种情况下，也是完全匹配的，递归函数返回true，否则返回false
- 否则，即sL!=s.length，pL==p.length：这种情况下，字符串s还没有匹配完，但是字符模式p消耗完了，这种情况下返回false
- 如果sL==s.length：这种情况下，字符串s已经完全被匹配完了(s的最后一个字符的索引为s.length-1)，但是字符模式p可能还有字符没有用完，需要分情况讨论
- 递归的终止条件找到了，接下来就是递归的转移过程了，此时，字符串s和字符模式p都有剩余字符，需要分三种情况，对于字符模式p，只有三种字符"?"，"*"，"a-z"
- 如果p[pL]=='?'：表示当前？可以匹配任意一个字符，一定能够匹配成功，所有直接return process(s,p,sL+1,pL+1)
- 如果p[pL]=='*'：可以选择，让当前的*匹配0个字符，1个字符，多个字符
- 匹配0个字符：p1=process(s,p,sL,pL+1)。会消耗掉一个*
- 匹配1个字符：p2=process(s,p,sL+1,pL+1)，会消耗掉一个*
- 匹配多个字符：p2=process(s,p,sL+1,pL)，这时，不消耗掉*，让其继续匹配
- 如果p1，p2，p3任意一个为true，则字符模式p是完全匹配字符串s的
- 最终返回p1||p2||p3
- 否则，即p[pL]是普通的小写字符：
- 如果p[pL]==s[sL]：return process(s,p,sL+1,pL+1)
- 否则：return false
超时代码：
class Solution {
public static boolean isMatch(String s, String p) {
return process(s.toCharArray(),p.toCharArray(),0,0);
}
public static boolean process(char[] s,char[] p,int sL,int pL){
if (sL==s.length){
if (pL==p.length){
return true;
}else {
while (pL<p.length){
if (p[pL]=='*'){
pL++;
}else {
break;
}
}
return pL>=p.length;
}
}
if (pL==p.length){
return false;
}
if (p[pL]=='?'){
return process(s,p,sL+1,pL+1);
}else if (p[pL]=='*'){
//匹配0个
boolean p1 = process(s,p,sL,pL+1);
//匹配一个
boolean p2 = process(s,p,sL+1,pL+1);
//匹配多个
boolean p3 = process(s,p,sL+1,pL);
return p1||p2||p3;
}else {
if (p[pL]==s[sL]){
return process(s,p,sL+1,pL+1);
}else {
return false;
}
}
}
}
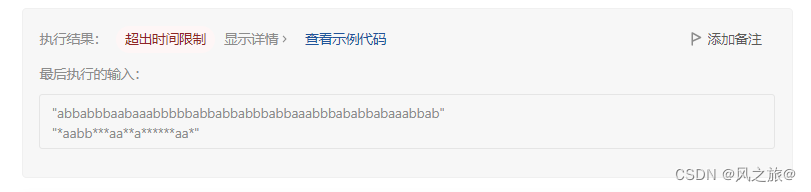时间超了，暴力递归的时间复杂度太高，有很多重复的递归。不过只要不是答案错误，说明算法整体思路是没有问题的，只是时间复杂度太高。。。。
注意：只要写出了递归解法，就可以根据递归直接修改为动态规划解法，步骤如下：
- dp数组的维度与大小：递归函数boolean process(char[] s,char[] p,int sL,int pL)中的一直在变化的参数只有两个sL和pL，所以只需要两个维度就可以表示所有的递归过程。右因为递归的终止条件为sL==s.length或者pL==p.length，即从0到s.length，0到p.length，所以使用dp[s.length+1][p.length+1]就可以保存所有的递归函数。其中dp[sL][pL]=process(char[] s,char[] p,int sL,int pL)，dp[i][j]表示字符模式p从索引j开始一直到结束的的子串是否完全匹配字符串s从索引i开始到结束的子串，如果完全匹配，返回true，否则，返回false
- dp数组的初始化值：递归方程的终止条件就是dp数组的初始值
- 递归方程的终止条件为
if (sL==s.length){ if (pL==p.length){ return true; }else { while (pL<p.length){ if (p[pL]=='*'){ pL++; }else { break; } } return pL>=p.length; } } if (pL==p.length){ return false; } - 所以dp数组的初始值为
boolean [][] dp = new boolean[s.length+1][p.length+1]; dp[s.length][p.length] = true; int i = p.length-1; //字符串s到达结尾 while (i>=0){ if (p[i]=='*'){ //虽然p还没有被消耗完，但是如果还没有被消耗的字符是*，这种情况也是完全匹配的 dp[s.length][i]=true; i--; }else { break; } } //字符串s到达结尾，p还没有到达结尾，并且，还没有被消耗的字符不是*，显然是不完全匹配的，返回false while (i>=0){ dp[s.length][i]=false; i--; } //字符模式p到达结尾，字符串s还没有匹配完，返回false for (i=0;i<s.length;i++){ dp[i][p.length]=false; }上述初始化后，可以得到如下的dp初始值
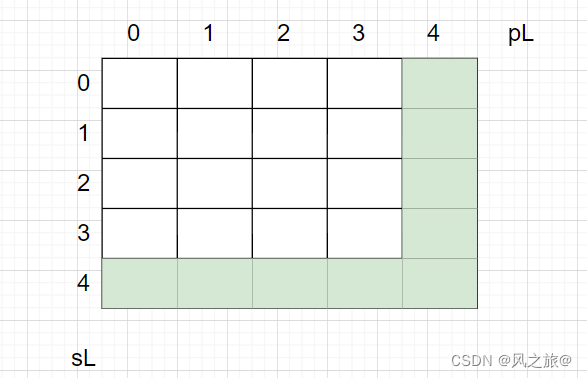
绿色表示dp数组中已经初始化的元素。
- 递归方程的终止条件为
- dp的状态转移：
在递归求解中，发现对于递归process(s,p,sL,pL)函数，在本次递归中可能会进入的递归有：process(s,p,sL+1,pL+1)，process(s,p,sl,pL+1)，process(s,p,sL+1,pL)。由dp[sL][pL]=process(char[] s,char[] p,int sL,int pL)得出，dp[sL][pL]得值可能与dp[sL+1][pL+1]，dp[sl][pL+1]，dp[sL+1][pL]有关如下图所示
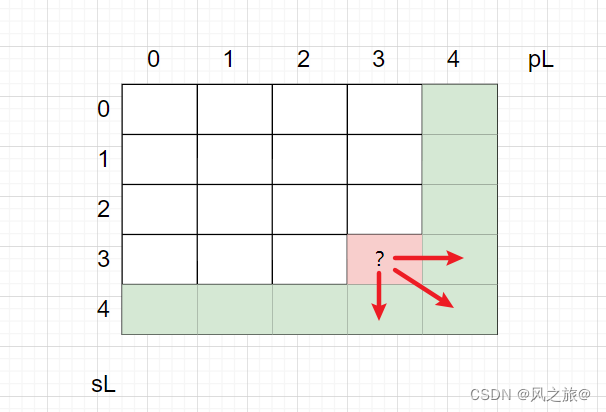
所以dp数组得更新方向也就确定，从右往左，从下往上(根据已知得值求解未知得值)。剩下得就是将出现return process()函数得地方修改为dp[sL][pL]=dp[][]就可以了
-
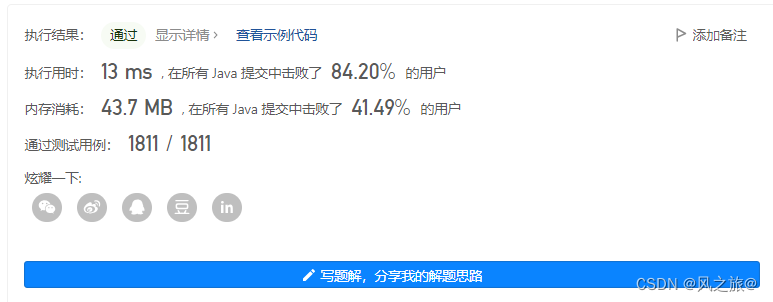
AC代码
class Solution {
public static boolean isMatch(String s, String p) {
return dp(s.toCharArray(), p.toCharArray());
}
public static boolean dp(char[] s, char[] p) {
boolean[][] dp = new boolean[s.length + 1][p.length + 1];
dp[s.length][p.length] = true;
int i = p.length - 1;
//字符串s到达结尾
while (i >= 0) {
if (p[i] == '*') {
//虽然p还没有被消耗完，但是如果还没有被消耗的字符是*，这种情况也是完全匹配的
dp[s.length][i] = true;
i--;
} else {
break;
}
}
//字符串s到达结尾，p还没有到达结尾，并且，还没有被消耗的字符不是*，显然是不完全匹配的，返回false
while (i >= 0) {
dp[s.length][i] = false;
i--;
}
//字符模式p到达结尾，字符串s还没有匹配完，返回false
for (i = 0; i < s.length; i++) {
dp[i][p.length] = false;
}
for (int sL = s.length - 1; sL >= 0; sL--) {
for (int pL = p.length - 1; pL >= 0; pL--) {
if (p[pL] == '?') {
dp[sL][pL] = dp[sL + 1][pL + 1];
} else if (p[pL] == '*') {
dp[sL][pL] = dp[sL][pL + 1] || dp[sL + 1][pL + 1] || dp[sL + 1][pL];
} else {
if (p[pL] == s[sL]) {
dp[sL][pL] = dp[sL + 1][pL + 1];
} else {
dp[sL][pL] = false;
}
}
}
}
return dp[0][0];
}
} 
从暴力递归到动态规划得过程中，完全没有求解dp状态转移方程，而是根据递归函数到dp的转换，这种方式对于求解不出dp状态转移方程的情况下非常有用！
