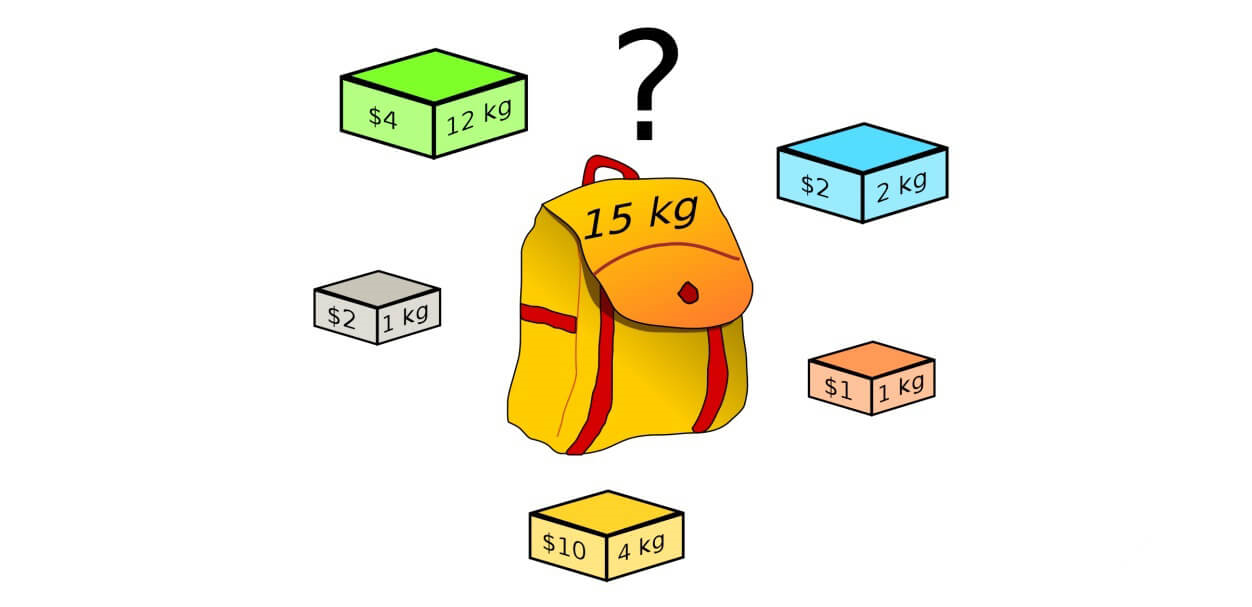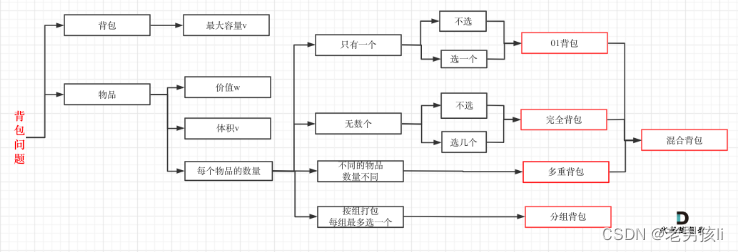
01背包:物品只能选一个
完全背包:物品可以选无数个
注:01背包与完全背包,不论是求背包装的最多物品的价值,还是求装满容量为bag的背包最多有几种方法,区别都在里层遍历背包时,01背包使用倒序遍历,完全背包使用正序遍历
一、01背包问题
1. 给定背包大小bag,求背包装的最多物品的价值
代码随想录 动态规划12题:01背包理论基础(滚动数组)
def test_1wei_bag_problem():
weight = [1, 3, 4] #物品所占体积
value = [15, 20, 30] #物品价值
bag = 4 #背包大小
dp = [0] * (bag + 1) #初始化迭代数组
for i in range(len(weight)): # 外层遍历物品
for j in range(bag, weight[i] - 1, -1): #里层遍历背包,背包要采用倒序遍历
dp[j] = max(dp[j],dp[j - weight[i]] + value[i])
#dp后面的参数永远是背包大小减物体重量
return dp[bag]
2.装满容量为bag的背包,最多有几种方法
代码随想录 动态规划16题:目标和
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
total_sum = sum(nums) # 计算nums的总和
if abs(target) > total_sum:
return 0 # 此时没有方案
if (target + total_sum) % 2 == 1:
return 0 # 此时没有方案
target_sum = (target + total_sum) // 2 # 目标和,相当于bag
dp = [0] * (target_sum + 1) # 创建动态规划数组,初始化为0
dp[0] = 1 # 当目标和为0时,只有一种方案,即什么都不选
for num in nums: #nums为物品重量与物品价值
for j in range(target_sum, num - 1, -1): #01背包采用倒序
dp[j] += dp[j - num] # 状态转移方程,累加不同选择方式的数量
return dp[target_sum] 二、完全背包
1. 给定背包大小bag,求背包装的最多物品的价值
代码随想录 动态规划18题:完全背包理论基础
def test_CompletePack():
weight = [1, 3, 4]
value = [15, 20, 30]
bagWeight = 4
dp = [0] * (bagWeight + 1) #迭代数组初始化
for i in range(len(weight)): # 外层遍历物品
for j in range(weight[i], bagWeight + 1): # 内层遍历背包容量,完全背包采用正序遍历
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp[bagWeight])
test_CompletePack()2.装满容量为bag的背包,最多有几种方法
代码随想录 动态规划19题:零钱兑换Ⅱ
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp = [0]*(amount + 1)
dp[0] = 1
for i in range(len(coins)): # 遍历物品
for j in range(coins[i], amount + 1): # 遍历背包
dp[j] += dp[j - coins[i]]
return dp[amount]3.完全背包排列问题:外层遍历背包容量,里层遍历物品种类
代码随想录 动态规划21题:组合总和Ⅳ
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
dp = [0] * (target + 1)
dp[0] = 1
for i in range(1, target + 1): # 外层遍历背包
for j in range(len(nums)): # 里层遍历物品
if i >= nums[j]:
dp[i] += dp[i - nums[j]]
return dp[target]