数据结构–线索二叉树的概念

二叉树的中序遍历序列

void InOrder(BiTree T)
{
    if (T != NULL)
    {
        InOrder(T->lchild); //递归遍历左子树
        visit(T); //访问根结点
        InOrder(T->rchild); //递归遍历右子树
    }
}

中序遍历序列:D G B E A F C

①如何找到指定结点p在中序遍历序列中的前驱?
②如何找到p的中序后继?

思路:
从根节点出发，重新进行一次中序遍历，指针q记录当前访问的结点,指针pre记录上一个被访问的结点
①当qp时，pre为前驱
②当prep时，q为后继

$缺点:找前驱、后继很不方便;遍历操作必须从根开始$

中序线索二叉树

图示说明:

中序遍历序列:D G B E A F C

$n个结点的二叉树，有n+1个空链域!可用来记录前驱、后继的信息$

$指向前驱、后继的指针称为"线索”$

线索二叉树的存储结构

图示说明:

typedef struct BiTNode
{
    ElemType data; //数据域
    struct BiTNode *lchild, *rchild; //左、右孩子指针
    struct BiTnode *parent; //父节点指针
}BiTNode, *BiTree;

typedef struct ThreadNode
{
    ElemType data;
    struct ThreadNode *lchild, *rchild;
    int ltag, rtag;
}ThreadNode, *ThreadTree; //左、右线索标志

中序线索二叉树的存储

先序线索二叉树

先序遍历序列:.A B D G E C F

先序线索二叉树的存储

后序线索二叉树

后序遍历序列:G D E B F C A

后序线索二叉树的存储

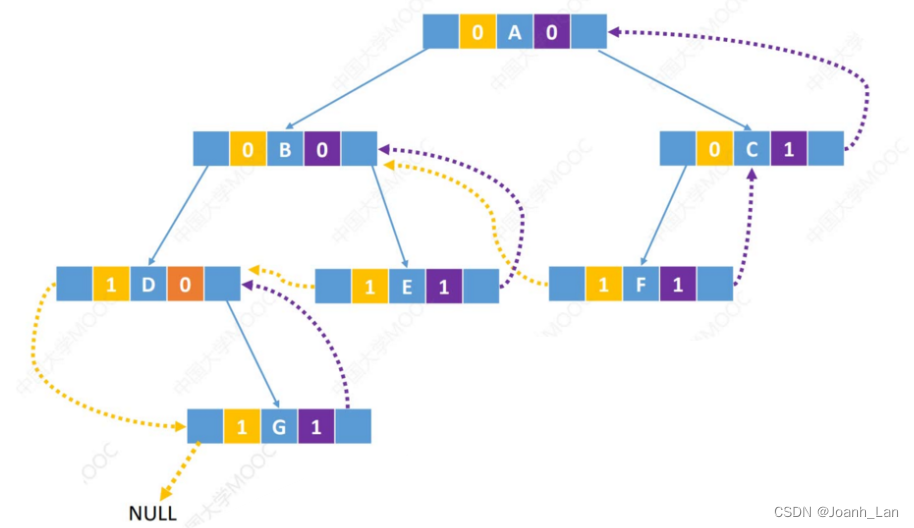
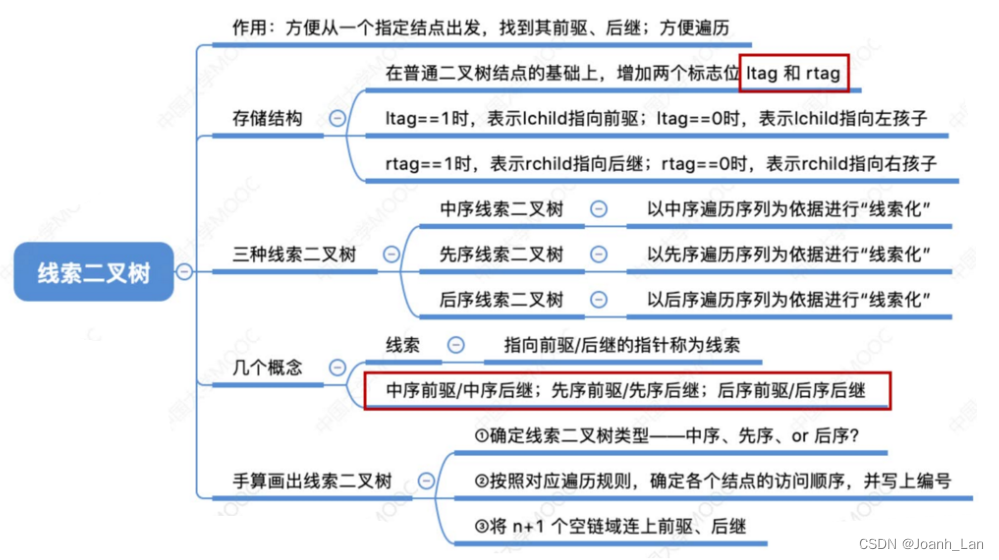
三种线索二叉树的对比

知识点回顾与重要考点