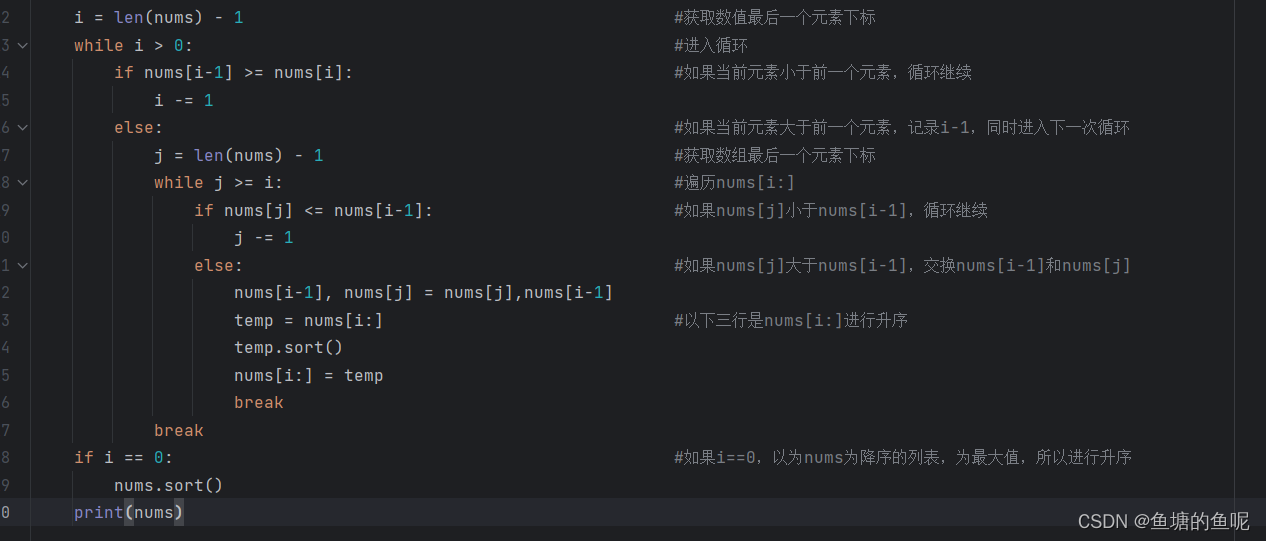
一，最长奇偶子数组

 看题可知可以使用暴力求解，从头开始遍历数组，另设一个变量来记录满足条件的子数组长度的最大值，将该变量不断与新得到的子数组长度比较，最终得到子数组长度的最大值。但是这样依次遍历的话，时间复杂度为O(n^2)。

设子数组的左下标为 left ，右下标为 right，在上面的解法中，如果一个子数组满足了条件，我们会重复计算[left+1，right]、[left+2，right]....[right，right] 这些子数组长度，因为我们要找到最长，所以这些子数组不用考虑，为了优化这一缺点，我们需要设置一个变量来存储子数组后面的第一个满足1，3条件的初始下标。优化后的时间复杂度为O(n)，代码如下：

class Solution {
    public int longestAlternatingSubarray(int[] nums, int threshold) {
        int i = 0;
        int ans = 0;
        while(i < nums.length){
            if(nums[i]>threshold || nums[i]%2 != 0){//筛选子数组的初始下标
                i++;
                continue;
            }
            int j = i;//记录子数组的初始下标
            i++;//避免出现 i+1 使数组下标越界
            //注意：这里没有写nums[i-1]<=threshold的原因是，我们已经在上面比较过了！！！
            while(i < nums.length && nums[i] <= threshold && nums[i]%2 != nums[i-1]%2){
                i++;
            }
            ans = ans > i - j ? ans : i - j;
        }
        return ans;
    }
}

二，和等于目标值的质数对

 在解决这道题之前，我们需要了解埃式筛，埃式筛是一种得到质数的算法，它的操作是：遍历[2，n]的数，将2的倍数全部删除，下一个遍历的值是3，将3的倍数全部删除，下一个遍历的值是5（因为4已经被删除了），再将5的倍数全部删除，依次类推，最终剩下的就是[2，n]的质数。

埃式筛的核心原理就是：一个质数的因数只有 1 和 它本身！！！所以只要能遍历到，就说明它是质数。

算法实现：

    public final static int MK = (int)1e6+1;//题目要求n 的值在[1,10^6]
    public final static int[] prime = new int[100001];//用来储存质数
    public static final boolean[] is_prime = new boolean[MK];//用来判断下标i是不是质数，false为是质数，true为不是质数
    static{
        int k = 0;
        for(int i=2; i<MK; i++){
            if(!is_prime[i]){
                prime[k++] = i;
                // for(int j=i*i; j <= MK-1; j+=i){
                //   is_prime[j] = true;
                //}
                //上面的写法如果i过大，j会超出int的最大值，从而导致下标越界
                for(int j=i; j <= (MK-1) / i; j++)
                    is_prime[i*j] = true;
            }      
        }
    }

当我们得到[1，n]的质数后，这道题就很简单了，遍历质数数组，将 X 赋值为质数，Y = N - X，如果Y也在质数数组中就说明[X，Y]是符合要求的质数对，将其添加到链表中。结束条件是 X < Y，因为题目要求按照非递减顺序排序。代码如下：

class Solution {
    public final static int MK = (int)1e6+1;
    public final static int[] prime = new int[100001];
    public static final boolean[] is_prime = new boolean[MK];
    static{
        int k = 0;
        for(int i=2; i<MK; i++){
            if(!is_prime[i]){
                prime[k++] = i;
                for(int j=i; j <= (MK-1) / i; j++)
                    is_prime[i*j] = true;
            }      
        }
    }
    public List<List<Integer>> findPrimePairs(int n) {
        List<List<Integer>> ans = new ArrayList();
        if(n%2 != 0){
            if( n>4 && !is_prime[n-2]){
                List<Integer> tmp = new ArrayList();
                tmp.add(2);
                tmp.add(n-2);
                ans.add(tmp);
                return ans;
            }
            return ans;
        }
        for(int i = 0; i < prime.length; i++){
            int x = prime[i];
            int y = n - x;
            if(x > y)break;
            if(!is_prime[y]){
                List<Integer> tmp = new ArrayList();
                tmp.add(x);
                tmp.add(y);
                ans.add(tmp);
            }
        }
        return ans;
    }
}

注意：这里的 if 语句是为了剪枝，不然会超出时间限制，其原理是 奇数A = 奇数B + 偶数C ，且奇数A只能有一个质数对，因为只有2既为偶数，也为质数，所以如果奇数B（即 A-2）是质数，则直接返回[2,n-2]，不是质数，就返回空。

三，不间断子数组

题目意思就是nums的不间断子数组要满足   子数组最大值 - 子数组最小值 <= 2

在写这道题之前，我们先举一个例子来理解一下题意，例如：nums = [ 5 , 4 , 2 , 4 ]

 但是这么做的时间复杂度为O(n^2) ，我们还可以优化，实际上当不满足条件时，我们只需要将 L 移动到当前子数组第二大值或者第二小值（第二大/小值离L近就移动到第二大/小值），依次类推，再画个图理解一下：

 

 在理解了这一点后，我们需要做的就是存储 [ L , R ] 的从大到小和从小到大的下标，然后不断的移动L，R就可以了。代码如下：

class Solution {
    public long continuousSubarrays(int[] nums) {
        int[] max = new int[nums.length];//存储子数组的从大到小的下标
        int[] min = new int[nums.length];//存储子数组的从小到大的下标
        int head = 0, headB = 0;
        int last = 0, lastB = 0;
        int L = 0;
        long ans = 0;
        for(int R=0; R<nums.length; R++){
            while(head < last && nums[max[last-1]]<nums[R]){
                last--;
            }
            while(headB < lastB && nums[min[lastB-1]]>nums[R]){
                lastB--;
            }
            a[last++] = R;
            b[lastB++] = R;
            while(head < last && headB < lastB && nums[max[head]]-nums[min[headB]] > 2){
                if(max[head]<min[headB]){
                    head++;
                }else{
                    headB++;
                }
                L = max[head] > min[headB] ? min[headB] : max[head];
            }
            ans += R - L + 1;
        }
        return ans;
    }
}