- 线性激活函数的局限性
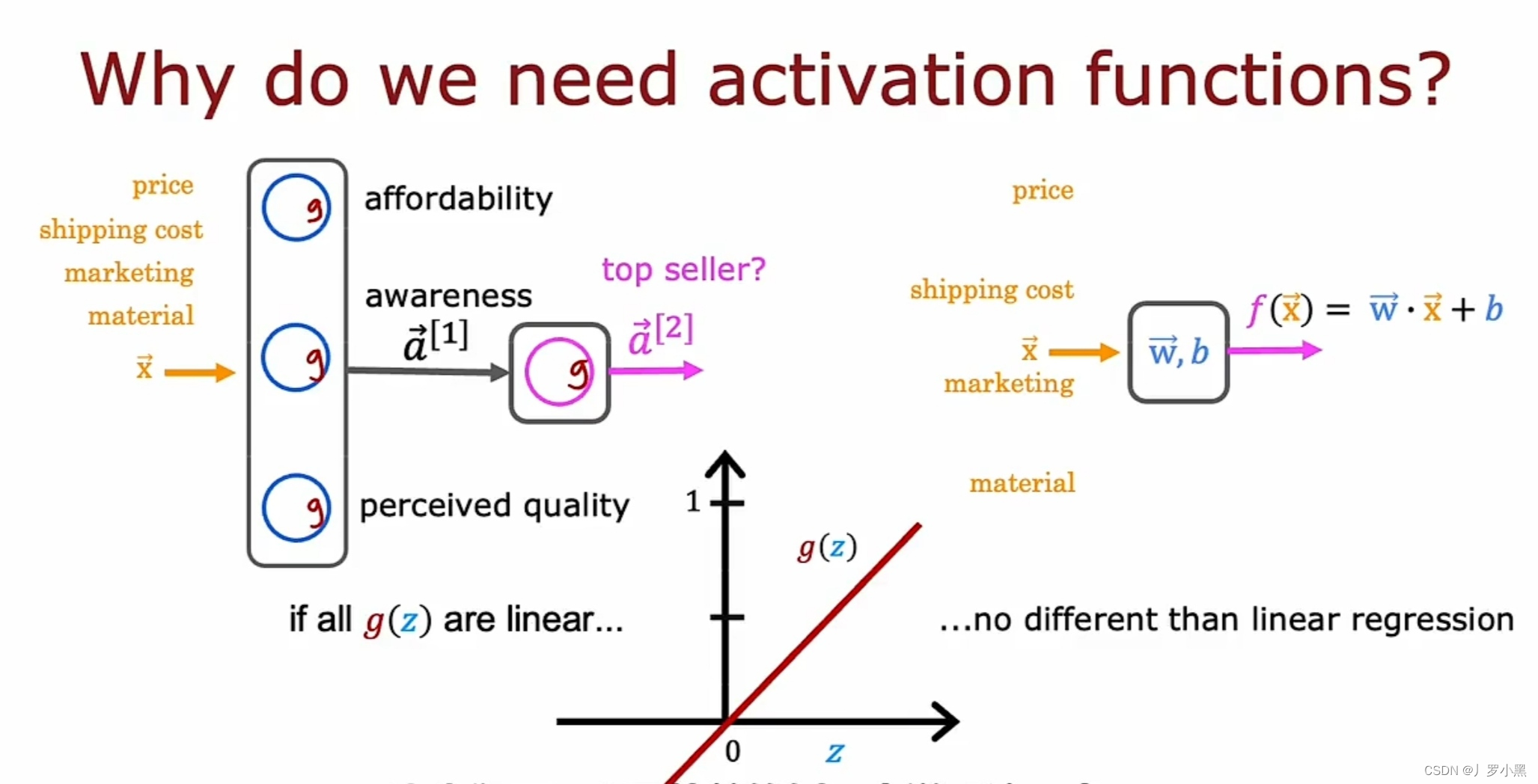
- 如果我们将神经网络模型中的所有激活函数都设为线性激活函数,那整个神经网络模型就跟线性回归模型极其相似,且它无法拟合比线性回归模型更复杂的关系
- 激活函数全设为线性回归激活函数的例子

- 若把a¹带入a²,则a²可简化为wx+b,这与其使用一个带有隐藏层和输出层的神经网络模型,不如直接使用线性回归模型。
- 原理:线性函数的线性函数就是一个线性函数
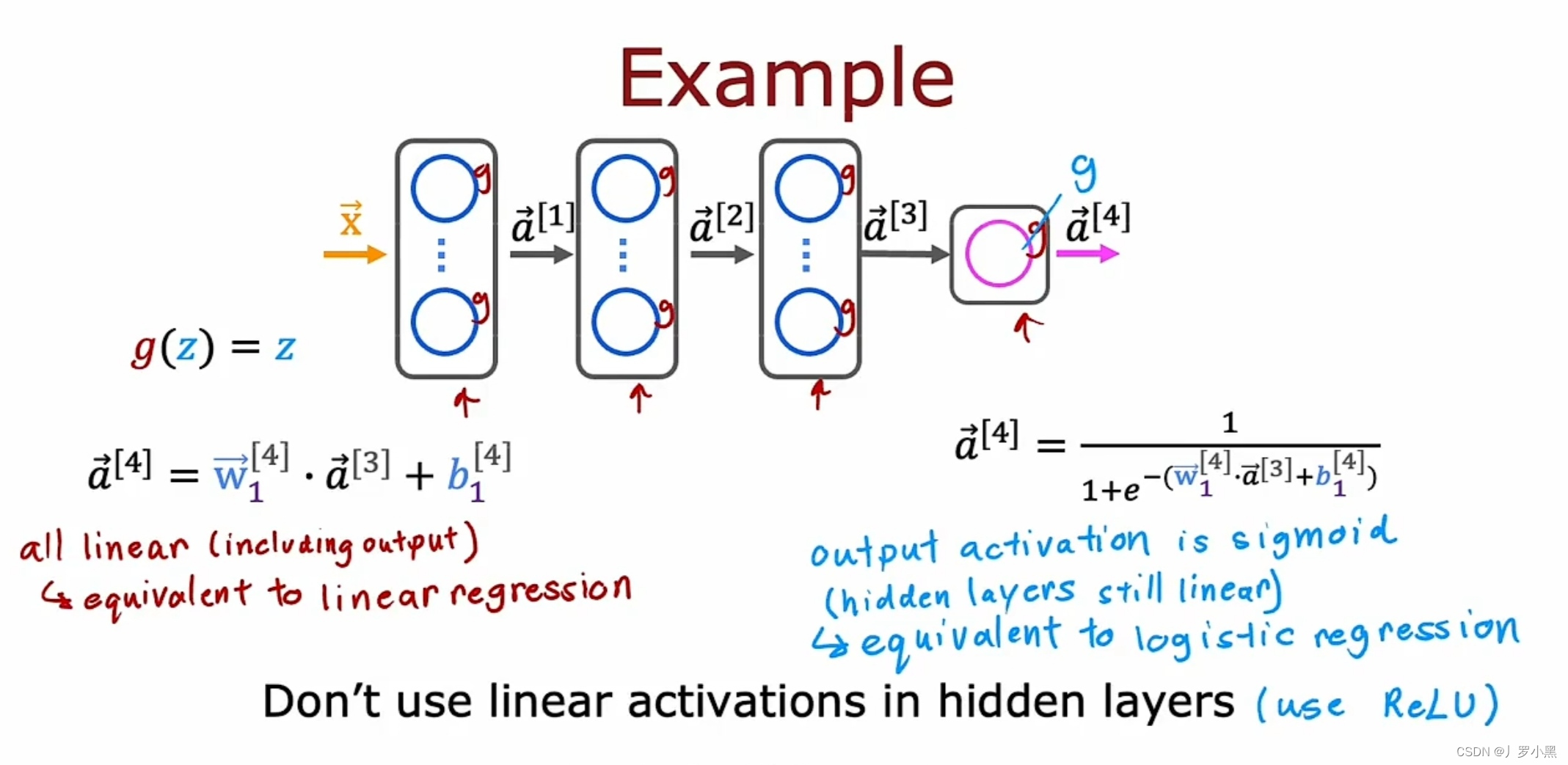
- 所以一般情况下,如果对神经网络模型的所有隐藏层使用线性激活函数,输出层也使用线性激活函数,那么该模型的计算结果等同于一个线性回归模型的结果,a⁴可以表示为wx+b
- 如果对神经网络模型的所有隐藏层使用线性激活函数,输出层使用sigmoid激活函数,那么该模型的计算结果等同于逻辑回归模型的结果,a⁴可以表示为g(z)
- 激活函数的目的是,在神经元的输出中引入非线性,使模型能够学习更复杂的输入和输出映射
- 解释:如果所有隐藏层都用线性回归激活函数,那么最后的结果可以用一个线性回归式子来表示,也就与隐藏层无关,只跟输出层有关。若输出层为线性回归,则模型整体等同于线性回归模型,若输出层为逻辑回归,则模型整体等同于逻辑回归模型,同时该模型也不能拟合比等价模型更复杂的关系
- 综上:不要在神经网络模型的隐藏层中使用线性回归激活函数,建议使用ReLU激活函数







![[NISACTF 2022]babyserialize(pop链构造与脚本编写详细教学)](https://img-blog.csdnimg.cn/7e6dd74221c64fc8bc4ee615897ba358.png)