第一种：

最简单的查看方法可以使用ls -ll、ls-lh命令进行查看，当使用ls -ll，会显示成字节大小，而ls- lh会以KB、MB等为单位进行显示，这样比较直观一些。

ls -ll

 

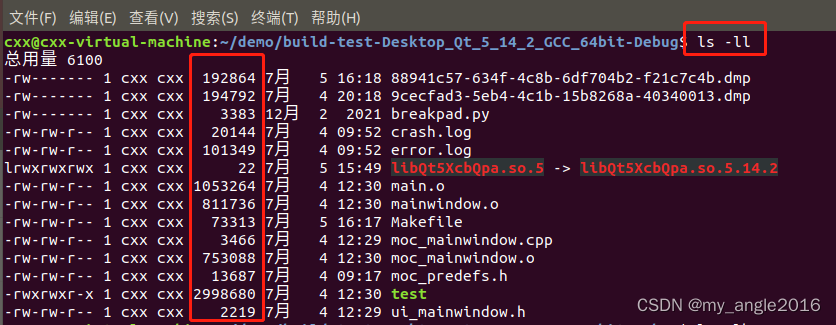
ls -lh 

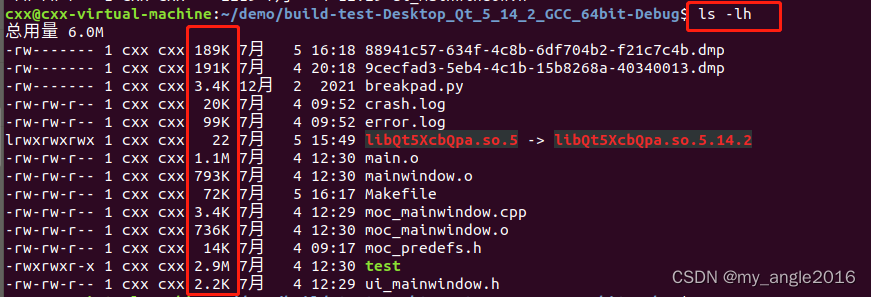
 第二种：

通过命令du -h –max-depth=1 *，可以查看当前目录下各文件、文件夹的大小，这个比较实用

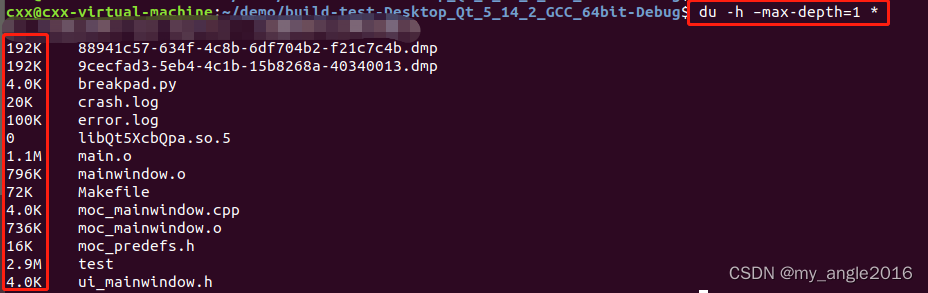
 第三种：

查询当前目录总大小可以使用du -sh，其中s代表统计汇总的意思，即只输出一个总和大小

 第四种：

同样，通过命令du -h –max-depth=0 *，可以只显示直接子目录文件及文件夹大小统计值

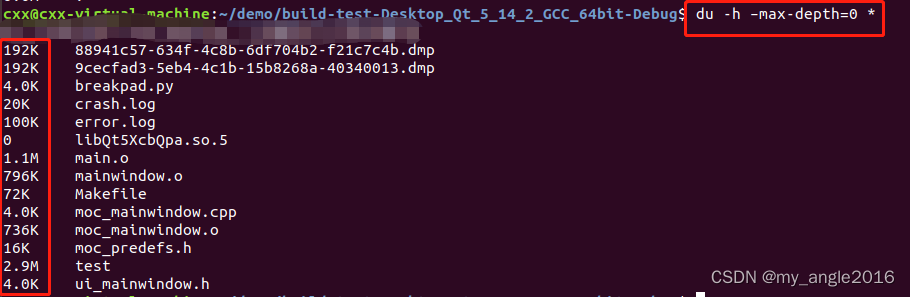
 第五种：

对于指定文件夹也可以指定显示层次深度，如du -h --max-depth=0 software/及du -h --max-depth=1 software/