基于梯度下降算法的无约束函数极值问题求解
- 1 知识预警
- 1.1导数
- 1.2偏导数
- 1.3方向导数
- 1.4梯度
- 2 梯度下降算法
- 3 无约束函数极值问题求解
- 3.1 算例1
- 3.1.1 Python编程求解
- 3.1.2 求解结果与可视化
- 3.2 算例2 Rosenbrock函数
- 3.2.1 Python编程求解
- 3.2.2 求解结果与可视化
1 知识预警
1.1导数
导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
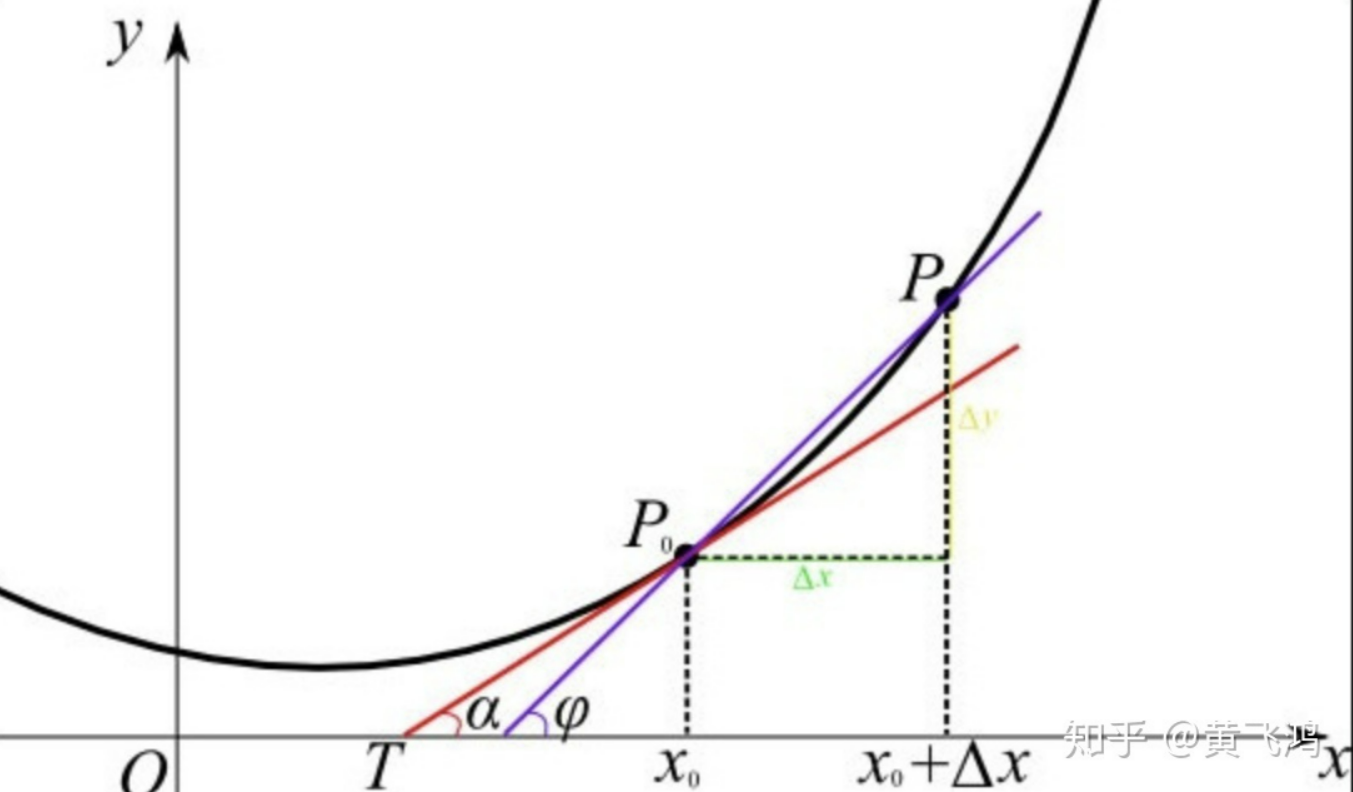
对于一条直线来说,求该直线的斜率就是找到该直线上两个点 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)和 ( x 2 , y 2 ) (x_2,y_2) (x2,y2),分别求出两点在 y y y和 x x x上的增量。因此斜率就是 y y y的改变量比上 x x x的改变量,即 k = tan θ = Δ x Δ y = y 2 − y 1 x 2 − x 1 k=\tan\theta =\frac{\Delta x}{\Delta y}=\frac{y_2-y_1}{x_2-x_1} k=tanθ=ΔyΔx=x2−x1y2−y1
对于不是直线该如何求斜率呢?因为曲线我们是不能笼统的随意找出两点,从而像直线一样求出它的斜率,而是以直代曲,近似的求出曲线在某一点的斜率。我们用的是该点的瞬时变化率,也就是求出该点处切线的斜率。
1.2偏导数
定义:设函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的某一领域内有定义,当 y y y固定在 y 0 y_0 y0,而 x x x在 x 0 x_0 x0处有增量时,相应地函数有增量: f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) f(x_0+\Delta x,y_0)-f(x_0,y_0) f(x0+Δx,y0)−f(x0,y0),如果 lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x \lim_{\Delta x \rightarrow 0 \frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}} limΔx→0Δxf(x0+Δx,y0)−f(x0,y0)存在,则称此极限为函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处对 x x x地偏导数,记为 ∂ z ∂ x ∣ ( x 0 , y 0 ) \frac{\partial z}{\partial x}|_{(x_0,y_0)} ∂x∂z∣(x0,y0), ∂ f ∂ x ∣ ( x 0 , y 0 ) \frac{\partial f}{\partial x}|_{(x_0,y_0)} ∂x∂f∣(x0,y0), z x ( x 0 , y 0 ) z_x(x_0,y_0) zx(x0,y0)或 f x ( x 0 , y 0 ) f_x(x_0,y_0) fx(x0,y0),即 f x ( x 0 , y 0 ) = lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x = d d x f ( x , y 0 ) ∣ x = x 0 f_x(x_0,y_0)=\lim_{\Delta x \rightarrow 0 \frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}}= \frac {\mathrm{d}}{\mathrm{d} x}f(x,y_0)|_{x=x_0} fx(x0,y0)=limΔx→0Δxf(x0+Δx,y0)−f(x0,y0)=dxdf(x,y0)∣x=x0。
同理,可定义函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处对 y y y的偏导数,为 lim Δ y → 0 f ( x 0 , y 0 + Δ y ) − f ( x 0 , y 0 ) Δ y \lim_{\Delta y \rightarrow 0}{ \frac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{\Delta y}} limΔy→0Δyf(x0,y0+Δy)−f(x0,y0),记为 ∂ z ∂ y ∣ ( x 0 , y 0 ) \frac{\partial z}{\partial y}|_{(x_0,y_0)} ∂y∂z∣(x0,y0), ∂ f ∂ y ∣ ( x 0 , y 0 ) \frac{\partial f}{\partial y}|_{(x_0,y_0)} ∂y∂f∣(x0,y0), z y ( x 0 , y 0 ) z_y(x_0,y_0) zy(x0,y0)或 f y ( x 0 , y 0 ) f_y(x_0,y_0) fy(x0,y0),即 f x y ( x 0 , y 0 ) = lim Δ y → 0 f ( x 0 , y 0 + Δ y ) − f ( x 0 , y 0 ) Δ y = d d y f ( x 0 , y ) ∣ y = y 0 f_xy(x_0,y_0)=\lim_{\Delta y \rightarrow 0}{ \frac{f(x_0 ,y_0+\Delta y)-f(x_0,y_0)}{\Delta y}}= \frac {\mathrm{d}}{\mathrm{d} y}f(x_0,y)|_{y=y_0} fxy(x0,y0)=limΔy→0Δyf(x0,y0+Δy)−f(x0,y0)=dydf(x0,y)∣y=y0。
如果函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在区域D内任意一点(x,y)处对x的偏导数都存在,那么这个偏导数就是x、y的函数,它就称为函数 z = f ( x , y ) z=f(x,y) z=f(x,y)对自变量x的偏导函数,简称偏导数,记作 ∂ z ∂ x \frac{ \partial z}{ \partial x} ∂x∂z, ∂ f ∂ x \frac{ \partial f}{ \partial x} ∂x∂f, z x z_x zx, f x ( x , y ) f_x(x,y) fx(x,y)。
同理,可以定义函数 z = f ( x , y ) z=f(x,y) z=f(x,y)对自变量y的偏导数,记作 ∂ z ∂ y \frac{ \partial z}{ \partial y} ∂y∂z, ∂ f ∂ y \frac{ \partial f}{ \partial y} ∂y∂f, z y z_y zy, f y ( x , y ) f_y(x,y) fy(x,y)。
偏导数的概念可以推广到二元以上函数,如u=f(x,y,z)在(x,y,z)处:
f
x
(
x
,
y
,
z
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
,
y
,
z
)
−
f
(
x
,
y
,
z
)
Δ
x
f_x(x,y,z) = \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x,y,z) - f(x,y,z)}{\Delta x}
fx(x,y,z)=Δx→0limΔxf(x+Δx,y,z)−f(x,y,z)
f
x
(
x
,
y
,
z
)
=
lim
Δ
y
→
0
f
(
x
,
y
+
Δ
y
,
z
)
−
f
(
x
,
y
,
z
)
Δ
y
f_x(x,y,z) = \lim_{\Delta y \rightarrow 0} \frac{f(x,y+\Delta y,z) - f(x,y,z)}{\Delta y}
fx(x,y,z)=Δy→0limΔyf(x,y+Δy,z)−f(x,y,z)
f
x
(
x
,
y
,
z
)
=
lim
Δ
x
z
→
0
f
(
x
,
y
,
z
+
Δ
z
)
−
f
(
x
,
y
,
z
)
Δ
z
f_x(x,y,z) = \lim_{\Delta xz \rightarrow 0} \frac{f(x,y,z+\Delta z) - f(x,y,z)}{\Delta z}
fx(x,y,z)=Δxz→0limΔzf(x,y,z+Δz)−f(x,y,z)
【注】偏导数只能表示多元函数沿某个坐标轴方向的导数,如对于二元函数 f ( x , y ) = x 2 + y 2 f(x,y)=x^2+y^2 f(x,y)=x2+y2, ∂ z ∂ x = 2 x \frac{\partial z}{\partial x}=2x ∂x∂z=2x表示函数沿着x轴方向的导数; ∂ z ∂ y = 2 y \frac{\partial z}{\partial y}=2y ∂y∂z=2y表示函数沿着y轴方向的导数;
1.3方向导数
除了沿坐标轴方向上的导数,多元函数在非坐标轴方向上也可以求导数,这种导数称为方向导数。很容易发现,多元函数在特定点的方向导数有无穷多个,表示函数值在各个方向上的增长速度。一个很自然的问题是:在这些方向导数中,是否存在一个最大的方向导数,如果有,其值是否唯一?为了回答这个问题,便需要引入梯度的概念。
1.4梯度
连续可微的多元函数 f ( x 1 , x 2 , ⋯ , x n ) f(x_1,x_2,\cdots,x_n) f(x1,x2,⋯,xn),用矢量表示其在点 ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cdots,x_n) (x1,x2,⋯,xn)的梯度为 ( ∂ f ∂ x 1 , ∂ f ∂ x 2 , ⋯ , ∂ f ∂ x n ) ( \frac{\partial f}{ \partial x_1},\frac{\partial f}{ \partial x_2},\cdots,\frac{\partial f}{ \partial x_n} ) (∂x1∂f,∂x2∂f,⋯,∂xn∂f),表示f在该点沿着梯度方向函数值增长最快,梯度的模增长的程度。 ( − ∂ f ∂ x 1 , − ∂ f ∂ x 2 , ⋯ , − ∂ f ∂ x n ) ( -\frac{\partial f}{ \partial x_1},-\frac{\partial f}{ \partial x_2},\cdots,-\frac{\partial f}{ \partial x_n} ) (−∂x1∂f,−∂x2∂f,⋯,−∂xn∂f)则表示负梯度,沿着负梯度方向函数值减小最快。
梯度是一个向量(矢量), 表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
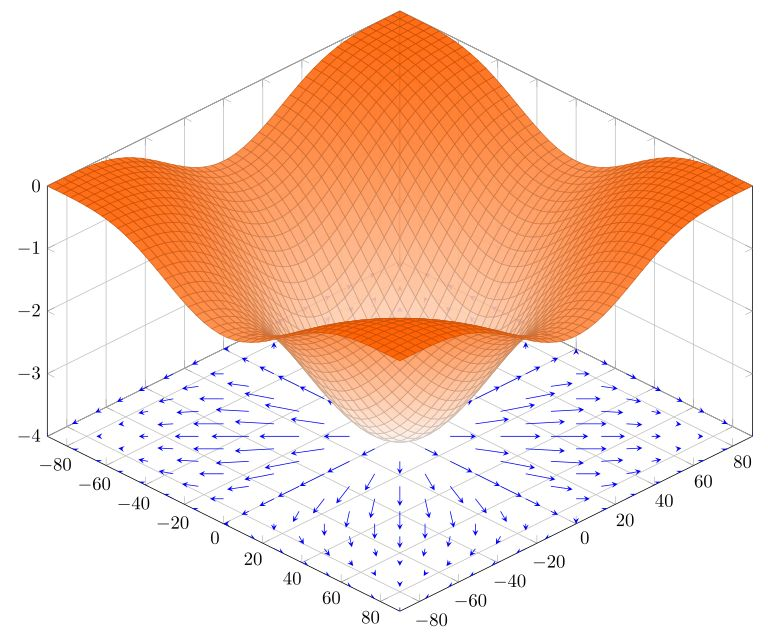
因此可以沿着梯度方向,搜索极值点(梯度下降算法)。
2 梯度下降算法
梯度下降法,又叫最速下降算法,是机器学习中一种常用到的算法,但其本身不是机器学习算法,而是一种求解的最优化算法,用于无约束多元函数求极值问题。在机器学习中,优化问题的目标函数通常是建立一个损失函数
L
(
θ
)
\mathcal L (\theta)
L(θ),使损失函数最小化
min
L
(
θ
)
\min \mathcal L(\theta)
minL(θ),梯度下降算法通过不断更新:
θ
t
:
=
θ
t
−
α
∇
L
(
θ
t
)
\begin{align} \theta_{t}:=\theta_{t}-\alpha \nabla \mathcal L(\theta_t) \end{align}
θt:=θt−α∇L(θt)
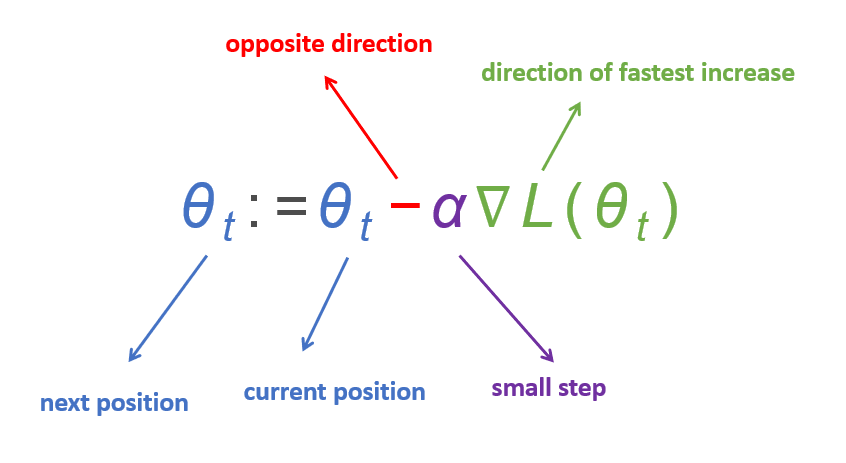
- 初始化迭代次数,学习率 α \alpha α,起点
- 求 L ( θ 1 , θ 2 , ⋯ , θ n ) \mathcal{L}(\theta_1,\theta_2,\cdots,\theta_n) L(θ1,θ2,⋯,θn)在点 ( θ 1 , θ 2 , ⋯ , θ n ) (\theta_1,\theta_2,\cdots,\theta_n) (θ1,θ2,⋯,θn)的梯度 ( ∂ L ∂ θ 1 , ∂ L ∂ θ 2 , ⋯ , ∂ L ∂ θ n ) ( \frac{\partial \mathcal{L}}{ \partial \theta_1},\frac{\partial \mathcal{L}}{ \partial \theta_2},\cdots,\frac{\partial \mathcal{L}}{ \partial \theta_n} ) (∂θ1∂L,∂θ2∂L,⋯,∂θn∂L);
- 对每一个 θ i \theta_i θi采用式(1)进行更新;
- 计算损失函数 L ( θ 1 , θ 2 , ⋯ , θ n ) \mathcal{L}(\theta_1,\theta_2,\cdots,\theta_n) L(θ1,θ2,⋯,θn)的值;
- 满足终止条件?是输出全局最优解,否转step2。
3 无约束函数极值问题求解
3.1 算例1
求函数 min f ( x , y ) = 2 ( x − 1 ) 2 + y 2 \min f(x,y)=2(x-1)^2+y^2 minf(x,y)=2(x−1)2+y2的极小值点,该函数的全局极小值点为 f ( 1 , 0 ) = 0 f(1,0)=0 f(1,0)=0
3.1.1 Python编程求解
"""
梯度下降SGD+多元函数求极值问题
求 f(x,y)=2(x-1)^2+y^2 的极小值
https://blog.csdn.net/MrKaj/article/details/115448804
"""
# 导入所需库
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings
def plotFig(midRes):
fig = plt.figure()
ax = Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(ax) # 设置图像为三维格式
X = np.arange(-10, 10, 0.1)
Y = np.arange(-10, 10, 0.1) # X,Y的范围
X, Y = np.meshgrid(X, Y) # 绘制网格
Z = 2 * (X - 1) ** 2 + Y ** 2 # f(x,y)=(sin(x)*sin(y))/(x*y),注意括号
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
lx = [i[0] for i in midRes]
ly = [i[1] for i in midRes]
lz = [i[2] for i in midRes]
ax.plot(lx, ly, lz, label='parametric curve', marker="o", linewidth=2, markersize=5, color='#000000')
# 绘制3D图,后面的参数为调节图像的格式
plt.show() # 展示图片
# 原函数
def f(x, y):
return 2 * (x - 1) ** 2 + y ** 2
# x方向上的梯度
def dx(x):
return 4 * x - 4
# y方向上的梯度
def dy(y):
return 2 * y
def gradient(x, y):
return 4 * x - 4, 2 * y
# 初始值
X = x0 = 10
Y = y0 = 10
# 学习率
alpha = 0.1
# 保存梯度下降所经过的点
midRes = [[x0, y0, f(x0, y0)]]
# 迭代30次
maxIter = 50
if __name__ == "__main__":
for i in range(maxIter):
pdx, pdy = gradient(X, Y)
X = X - alpha * pdx
Y = Y - alpha * pdy
Z = f(X, Y)
print(u"iter=%d x=%f y=%f z=%f" % (i, X, Y, Z))
midRes.append([X, Y, Z])
# 打印结果
print(u"最终结果为:(x,y,z)=(%.5f, %.5f, %.5f)" % (X, Y, f(X, Y)))
plotFig(midRes)
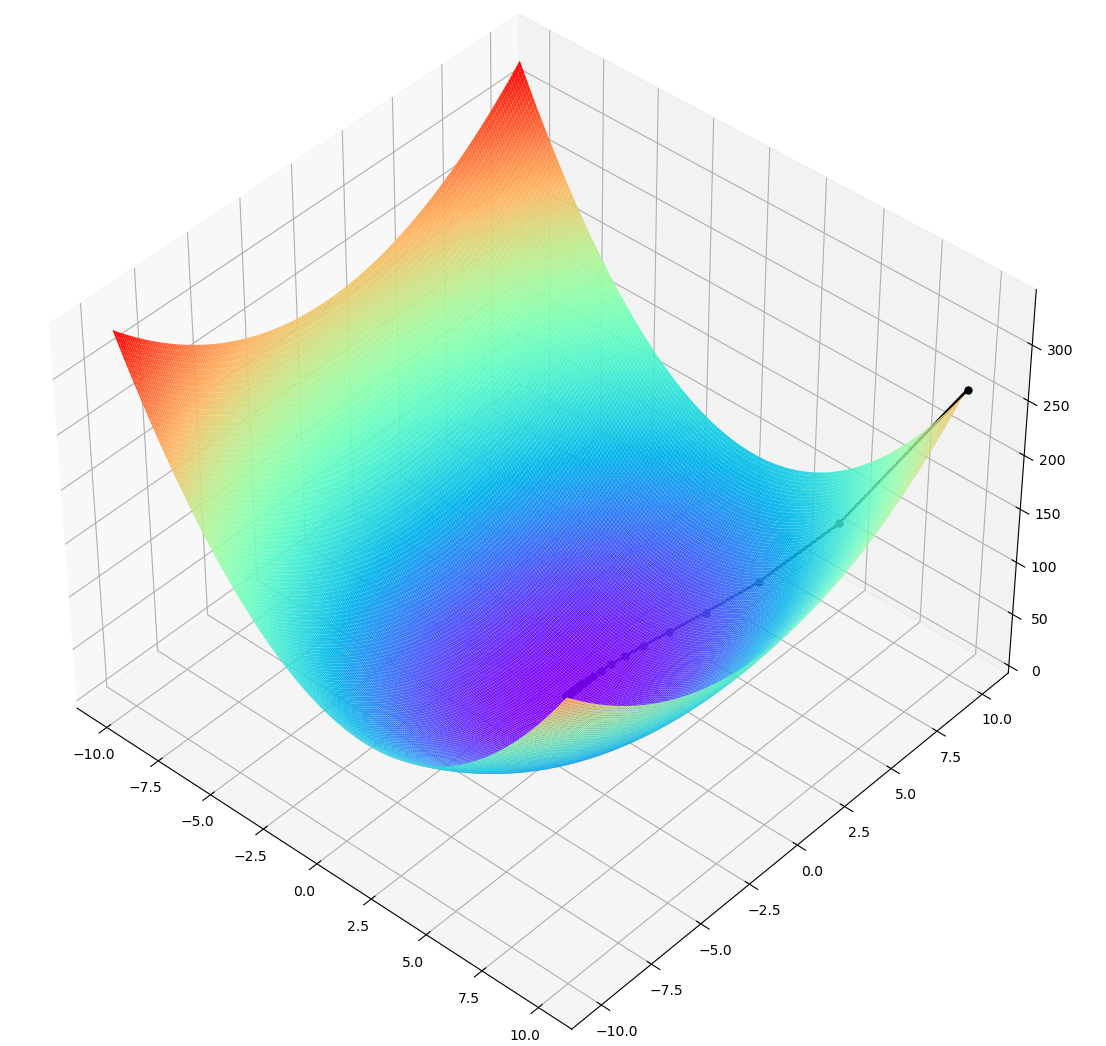
3.1.2 求解结果与可视化
iter=49 x=1.000000 y=0.000143 z=0.000000
最终结果为:(x,y,z)=(1.00000, 0.00014, 0.00000)
3.2 算例2 Rosenbrock函数
在数学最优化中,Rosenbrock函数是一个用来测试最优化算法性能的非凸函数,由Howard Harry Rosenbrock在1960年提出 。也称为Rosenbrock山谷或Rosenbrock香蕉函数,也简称为香蕉函数。Rosenbrock函数的每个等高线大致呈抛物线形,其全域最小值也位在抛物线形的山谷中(香蕉型山谷),位于 (x,y)=(1,1)点,数值为f(x,y)=0,图像如下图所示:
:
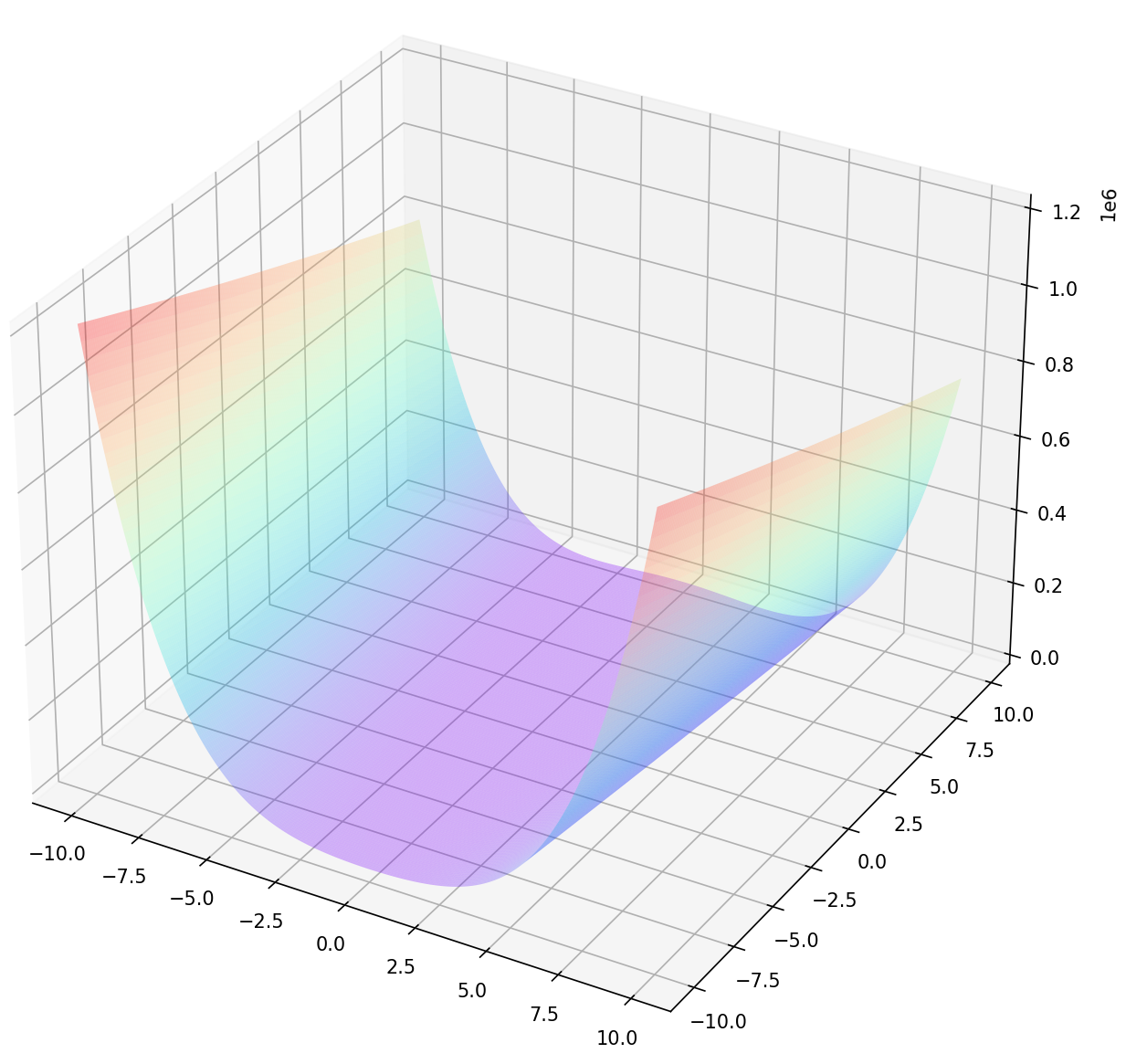
3.2.1 Python编程求解
"""
梯度下降法
f(x,y)=(1-x)^2+100(y-x^2)^2
"""
import numpy as np
from matplotlib import pyplot as plt, ticker
from mpl_toolkits.mplot3d import Axes3D
def plotFig(f, midRes=None):
fig = plt.figure()
ax = Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(ax) # 设置图像为三维格式
X = np.arange(-1, 1, .1)
Y = np.arange(-1, 1, .1) # X,Y的范围
X, Y = np.meshgrid(X, Y) # 绘制网格
Z = f(X, Y)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap="rainbow", alpha=0.3) # alpha控制透明度
lx = [i[0] for i in midRes]
ly = [i[1] for i in midRes]
lz = [i[2] for i in midRes]
ax.plot(lx, ly, lz, label='parametric curve', marker="*", linewidth=1, markersize=1, color='#000000')
plt.show()
def f(x, y):
return (1 - x) ** 2 + 100 * (y - x ** 2) ** 2
def gradient(x, y):
return 400 * x * (x ** 2 - y) + 2 * x - 2, 200 * (y - x ** 2)
if __name__ == "__main__":
X = x0 = -1
Y = y0 = -1
alpha = 0.002
midRes = [[x0, y0, f(x0, y0)]]
maxIter = 10000
for i in range(maxIter):
pdx, pdy = gradient(X, Y)
X = X - alpha * pdx
Y = Y - alpha * pdy
Z = f(X, Y)
print(u"iter=%d x=%f y=%f z=%f" % (i, X, Y, Z))
midRes.append([X, Y, Z])
print(u"最终结果为:(x,y,z)=(%.5f, %.5f, %.5f)" % (X, Y, f(X, Y)))
plotFig(f, midRes)
3.2.2 求解结果与可视化
iter=9999 x=0.999906 y=0.999811 z=0.000000
最终结果为:(x,y,z)=(0.99991, 0.99981, 0.00000)