文章目录
- 一、01背包
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 二、416. 分割等和子集
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 三、494. 目标和
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 四、1049. 最后一块石头的重量 II
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 总结
一、01背包
1.题目简介
DP41 【模板】01背包
本题来源于牛客网,大家可以通过上面的链接直接打开做题页面进行练习。



2.解题思路
3.代码
#include <iostream>
using namespace std;
#include<vector>
int main() {
int n, V;
cin>>n;//物品个数
cin>>V;//背包体积
vector<int> v(n, 0);//存物品体积
vector<int> p(n, 0);//存物品价值
for(int i =0;i < n; ++i)
{
cin>>v[i];//体积
cin>>p[i];//价值
}
//第一问
vector<int> v2(V + 1, 0);
vector<vector<int>> dp1(n + 1, v2);//dp[i][j]表示体积为j - 1的背包可以装的0~i - 1的物品的最大总价值是多少
for(int i = 1;i <= n; ++i)//二维dp数组的方法
{
for(int j = 0;j <= V ; ++j)
{
dp1[i][j] = dp1[i - 1][j];
//放不放当前物品(i物品)
//1.放; 2.不放
if(j >= v[i - 1])
dp1[i][j] = max(dp1[i - 1][j - v[i - 1]] + p[i - 1], dp1[i][j]);
}
}
cout<<dp1[n][V]<<endl;
//第二问
vector<int> dp2(V + 1, -1);
//初始化,将背包体积为0情况初始化为0(背包装满的总价值最大为0)
dp2[0] = 0;
for(int i = 1;i <= n; ++i)//一维dp数组的方法
{
for(int j = V;j >= v[i - 1]; --j)
{
//放不放当前物品(i物品)
//1.放; 2.不放
if(dp2[j - v[i - 1]] != -1)
{
dp2[j] = max(dp2[j - v[i - 1]] + p[i - 1], dp2[j]);
}
}
}
cout<< (dp2[V] == -1 ? 0 : dp2[V]) <<endl;
return 0;
}
4.运行结果
二、416. 分割等和子集
1.题目简介
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。

2.解题思路
3.代码
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for(auto& e : nums)
{
sum += e;
}
if(sum % 2 != 0) return false;//如果不能被2整除,则该数组不能被分割成两个元素和相等的子集
int target = sum / 2;//此时只需要判断数组中元素是否可以正好相加得到target
vector<int> dp(target + 1, 0);
//dp[j]表示体积为j背包最大能装多少质量
for(int i = 0;i < nums.size(); ++i)
{
for(int j = target;j >= nums[i]; --j)
{
dp[j] = max(dp[j - nums[i]] + nums[i], dp[j]);
}
}
return dp[target] == target;
}
};
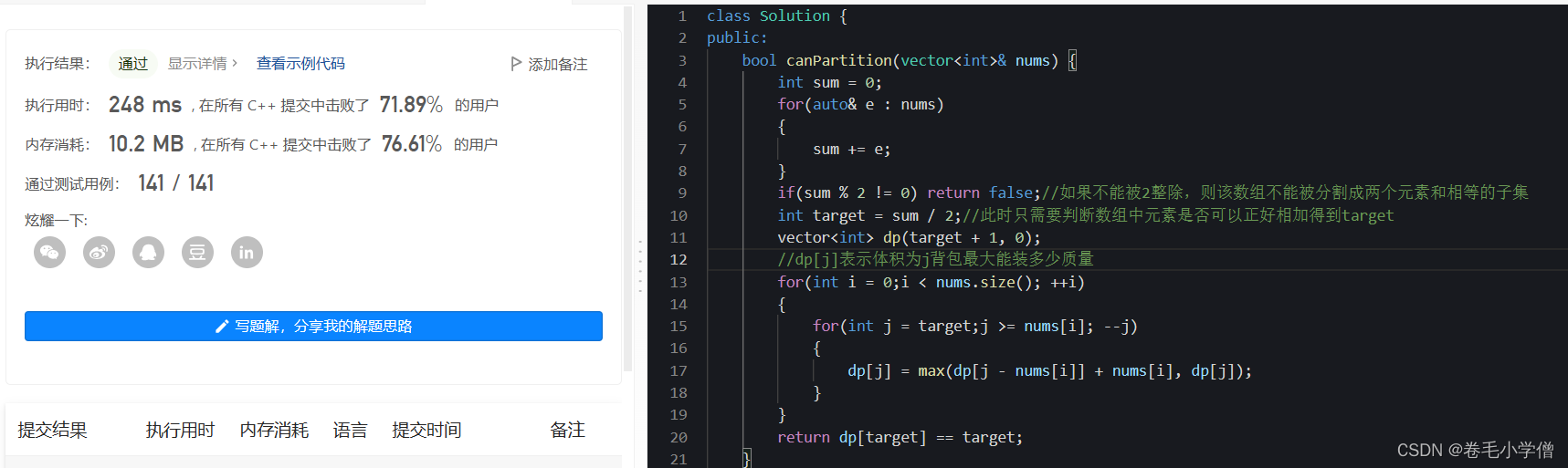
4.运行结果
三、494. 目标和
1.题目简介
494. 目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

2.解题思路
3.代码
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
//根据题意,我们可以将数组的元素分为两个子集,一个是正数子集,一个是负数子集(都是绝对值,即不带符号的内中)
//正数子集元素和 + 负数子集元素和 = nums数组的元素和(sum);
//正数子集元素和 - 负数子集元素和 = target;
//推出正数子集元素和num = (sum + target) / 2;
//然后计算有多少种nums中元素的组合方法可以使正数子集满足num
int sum = 0;
for(auto& e : nums)
{
sum += e;
}
if(sum < abs(target)) return 0;//如果数组元素之和小于target绝对值之和,则不可能满足条件
if((sum + target) % 2 != 0) return 0;//没有符合条件的正数子集之和
int num = (sum + target) / 2;
vector<int> dp(num + 1, 0);//dp[j]表示有多少种方法可以使子集之和为j
dp[0] = 1;//如果它是0,则会导致后面的推导结果错误
for(int i = 0;i < nums.size(); ++i)
{
for(int j = num;j >= nums[i]; --j)
{
dp[j] += dp[j - nums[i]];//要计算有多少中方式,因此要用+
}
}
return dp[num];
}
};
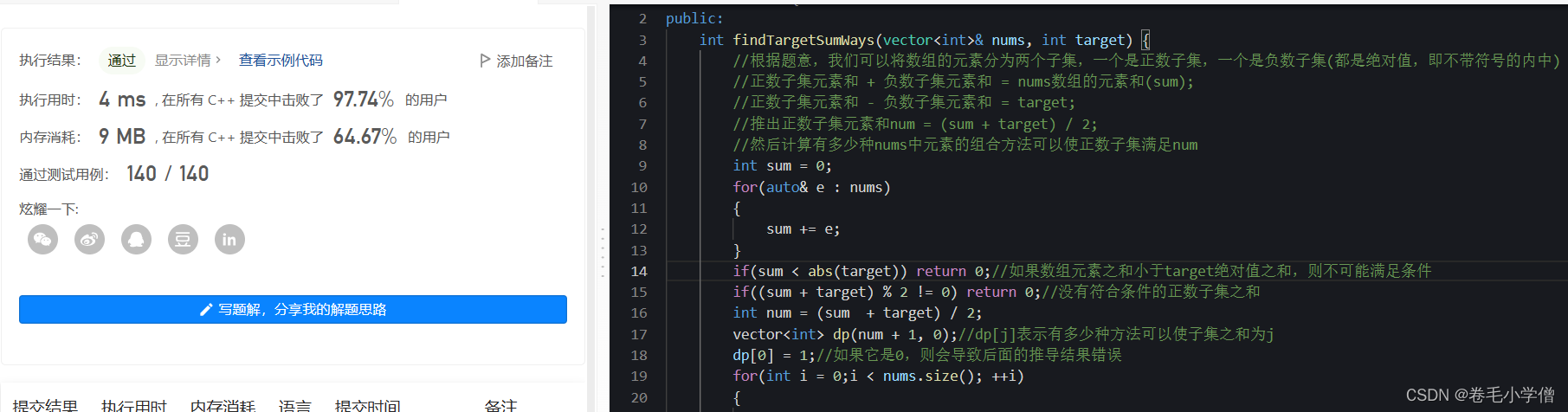
4.运行结果
四、1049. 最后一块石头的重量 II
1.题目简介
1049. 最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。

2.解题思路
3.代码
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
//根据题意,我们发现两个重量相近的石头粉碎的越多(即,剩余的重量越少)
//因此我们可以将所有石头分为重量相近的两份,这样两份石头进行粉碎,得到的就是最小可能的重量
//1.先计算所有石头的重量之和sum,再计算出重量之和的一半sum/2设为target;
int sum = 0;
for(auto& e : stones)
{
sum += e;
}
int target = sum / 2;
//2.用数组中的石头尽可能的取填充target,计算出最多可以放置的石头重量num;
vector<int> dp(target + 1, 0);
for(int i = 0;i < stones.size(); ++i)
{
for(int j = target;j >= stones[i]; --j)
{
dp[j] = max(dp[j - stones[i]] + stones[i], dp[j]);//放不放当前石头
}
}
int num = dp[target];
//3.num就是两份石头中重量相对较小的一份,则粉碎后最终剩余的石头重量为(sum - num) - num =》sum - 2 * num。
return sum - 2 * num;
}
};
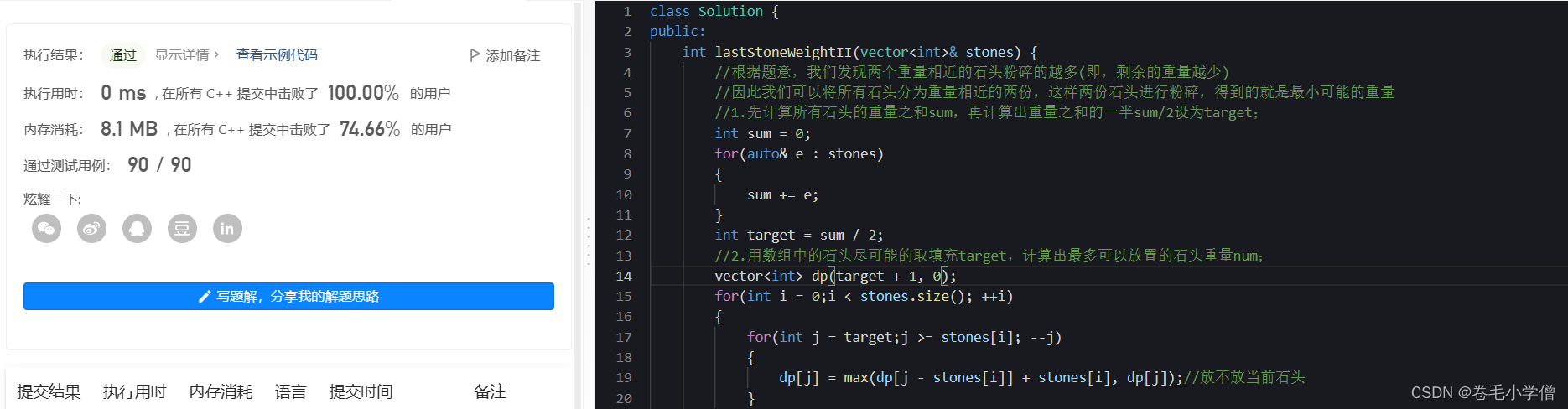
4.运行结果
总结
今天是算法练习的第15天。
千淘万漉虽辛苦,吹尽狂沙始到金 ,继续加油。
来源:力扣(LeetCode),著作权归领扣网络所有。
如果本篇文章对你有所启发的话,希望可以多多支持作者,谢谢大家!