1.简述

      

BP神经网络现在来说是一种比较成熟的网络模型了,因为神经网络对于数字图像处理的先天优势,特别是在图像压缩方面更具有先天的优势,因此,我这一段时间在研究神经网络的时候同时研究了一下关于BP网络实现图像压缩的原理和过程,并且是在MATLAB上进行了仿真的实验,结果发现设计的BP神经网络具有不错的泛化能力,对于用于图像压缩方面的效果还不错.

BP神经网络的模型的架构和训练的原理

BP神经网络是现在目前的发展的比较成熟的神经网络之一了,也是一种比较给力的非线性的可微分函数进行权值修正和调整的多层前馈人工神经网络,经得住严密的数学逻辑推导,在很多的模式识别的书中和很多的数据压缩的论文中得以大量的广泛和认同.BP神经网络算法主要的特点是输入信号的正向传递,误差的反向传播.BP网络的学习算法的本质其实就是把样本集合的输入输出问题变换为一个非线性优化的问题.其中分为三层的网络结构,包括输入层,隐藏层,输出层这样的三层.典型的一个网络模型的结构可以由下边的部分构成:

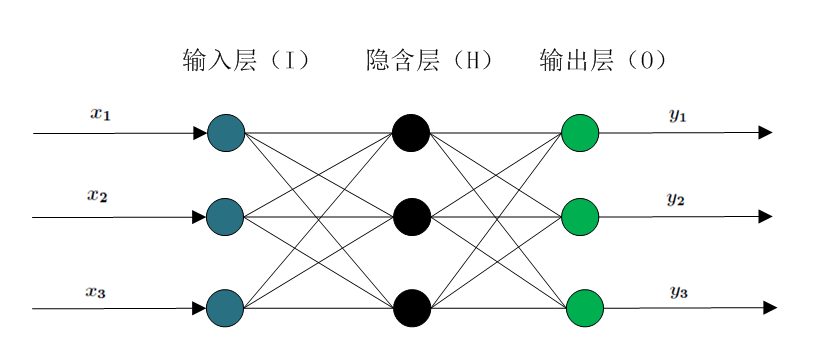
首先说一下前向传播:

首先在BP的神经网络模型中我们现在假设为L层,其中他的输入层是第1层,输出层是最后一层也就是L层,隐藏层的话其实就是从第2层到第L-1层了.要是在输出层的第K个神经单元,就可以简单的表示为

这个上标表示为层数,下标表示为第K个神经元,同理,其他的层数和神经元也都可以如此概述.这样的话对于第L层的神经元个数就可以用|L|来表示.即第L层的第J个神经元的输入与输出的关系如下图所示:

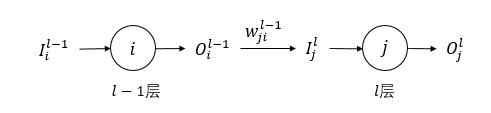
其中

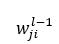
b表示为第L层的第J个神经元与L-1层第J个神经元的链接权重.

而其输出的Oij如下所示,其中f是激励函数

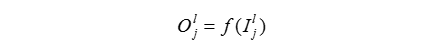
在神经网络中我们有很多的激活函数可以选择,但是我们在这里还是选择使用sigmood函数,为什么选用这个函数?因为在我搜集了很多资源来看,如果我们使用一些其他的激活函数或者直接放弃使用激活函数,不过我们使用多少次隐藏层,我们最终得到的仍然是一个线性的函数,但是在使用非线性的sigmoid函数以后,就不会有这个问题,我们的网络也可以去拟合非线性的函数.

在这里我们只需要记住sigmoid函数的推导,因为在接下来的反向传播中我们要去使用.

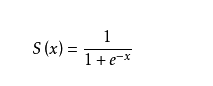
求导以后:

反向传播

关于反向传播,这个部分大概是整个BP神经网络的精华所在了.那么反向传播究竟是个什么东西呢?其实反向传播就是通过最后的误差来更新权值.打个比方,你现在是个学生,学校里搞了一大堆试卷,发给你们考试以后你们考完发现取得的效果并不好,当校长看到成绩单后,校长很生气,校长就说了,年级主任你去给我找问题,年级主任然后就跟班主任说你给我去找问题,,,一直到你们这些学生,老师让你们去改.这样对应的就是我们神经网络的输入层一直改到输出层.在这里使用到的一个重要的法则就是梯度下降法则.

梯度下降法,大学高数的知识,其实就是你更新权重的同时不能更新,而是按照梯度的方向更新才能够给更新权重,能够获得更多的收敛.公式如下:

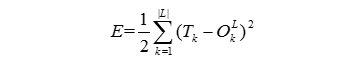
这里有一个负梯度方向需要说明一下,因为你的学习速率是大于0的,对于误差E来说,他对W的偏导数就必须要大于0这样也就是说,误差随着权重的增大而增大,那我们就需要通过减少权重来减小误差,所以W的变化率需要小于0,当然,如果我们要求某某某的最大值的话,也可以使用正梯度.

直观上来看神经网络的每个神经元的权重更新都是通过误差的偏导来更新的,在这里我们引入一个新的变量误差,对于第l层的第j个神经元的误差定义为

这样的权重更新过程可以为:

在这里我们需要用到的就是链式求导法则,具体如下:

根据sigmoid函数的求导公式,并且对于误差进行偏导,我们就可以得到第L层的神经元的误差项:

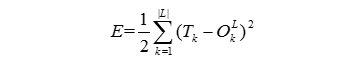
所以就能够得到输出层上一层与输出的权重更新公式:

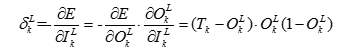
所以就能够得到输出层上一层与输出的权重更新公式:

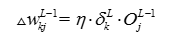
对于隐藏层,我们需要在求导时对于他的输出层单元的每个误差影响进行叠加,与输出层类似,不再赘述.

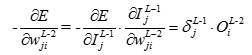
对于第L-1层的第j个神经元的误差项来说,由于每个神经元连接到输出层的每个单元,因此我们要对输出层的|L|个单元进行求和,从而得到了误差项的计算公式:

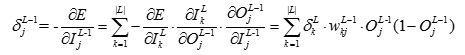
所以便得到了L-2与L-1层的链接权重的公式:

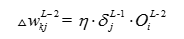
而对于其他层,我们进行推广就可以得到第I层第J个的神经单元的误差公式额权重更新公式:

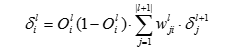
对于推导过程，简单的来说就是链式求导，由上面公式我们可以看出反向传播也是求导，只是对于隐层以及输入层来说，它们所产生的误差在传播过程中能够影响每一个最终的输出层单元，所以我们需要对其产生的误差求和。反向传播的前提是前向传播，而前向传播的公式相信大家很容易都能记住，而反向传播其实就是对前向传播的公式链式求导,只需要注意到求导过程中对于w对输出层的影响来判断什么时候需要进行求和操作就可以.

基于MATLAB的BP神经网络图像压缩过程的分析:

因为在MATLAB上应用BP神经网络对于数字图像进行压缩主要包括训练样本构造,仿真以及图像重建这三个环节.

训练样本的构建

因为我的机器的性能不够,考虑到需要将整幅图像中的所有像素数据都需要作为BP网络的输入数据,为了控制整个网络的训练规模和训练速度,因此对于图像进行分块化处理,但是考虑到临近像素之间的相关性和差异性,因此小图像的所占的像素比例不应该太大,假设一个图像是由N*N个像素构成,将整个图像切割为M个规则大小的小图像块,其中每个图像由n*n个像素构成,将每个小图像的数据重构为一个列向量,作为样本的训练向量,然后进行归一化数据处理.

这里用的是最值线性函数转换法,即:

Y(k)={X(k)-X(min)}/{X(max)-X(min)}

其中X(k)是转换之前的数据,Y(k)是转换之后的数据,X(min),X(max)是整个数据集合里边的最小值和最大值.通过归一化,可以将每个训练向量的像素值归一到[0,1]的范围内.

2:在创建并且训练好符合条件的BP网络后,使用上边提到Sigmoid对于归一化后的处理的图像数据进行仿真压缩,输出仿真向量,然后通过图像重建来还原为一幅完整的图像数据.

3:现在以静态的图像进行试验,控制大小为128*128,先将整幅图像分隔成为4*4的小图像快,再将每个小图像转化为16*1的列向量,统一归一化处理进行作为网络的输入的样本,按照上述的操作进行分析,创建BP网络,进行训练,这一次压缩比为4.

2.代码

%% 清理
clear,clc
close all

%% 载入数据
col=256;
row=256;
I=imread('lena.bmp');
load comp
com.lw=double(com.lw)/63;
com.b=double(com.b)/63;
com.d=double(com.d)/63;
com.lw=com.lw*(maxlw-minlw)+minlw;
com.b=com.b*(maxb-minb)+minb;
com.d=com.d*(maxd-mind)+mind;

%% 重建
for i=1:4096
   Y(:,i)=com.lw*(com.d(:,i)) +com.b;
end

%% 反归一化
Y=uint8(Y*255);

%% 图像块恢复
I1=re_divide(Y,col,4);

%% 计算性能
fprintf('PSNR :\n  ');
psnr=10*log10(255^2*row*col/sum(sum((I-I1).^2)));
disp(psnr)
a=dir();
for i=1:length(a)
   if (strcmp(a(i).name,'comp.mat')==1) 
       si=a(i).bytes;
       break;
   end
end
fprintf('rate: \n  ');
rate=double(si)/(256*256);
disp(rate)
figure(1)
imshow(I)
title('原始图像');
figure(2)
imshow(I1)
title('重建图像'); 
 

3.运行结果