文章目录
- 二三树
- 二三树的性质
- 二三树一个简单的插入例子
- 二三树的特点
- 红黑树
- 红黑树的特点
- 红黑树的节点
- 红黑树的插入操作
- 1. 左旋
- 2. 右旋+颜色翻转
- 3. 颜色翻转
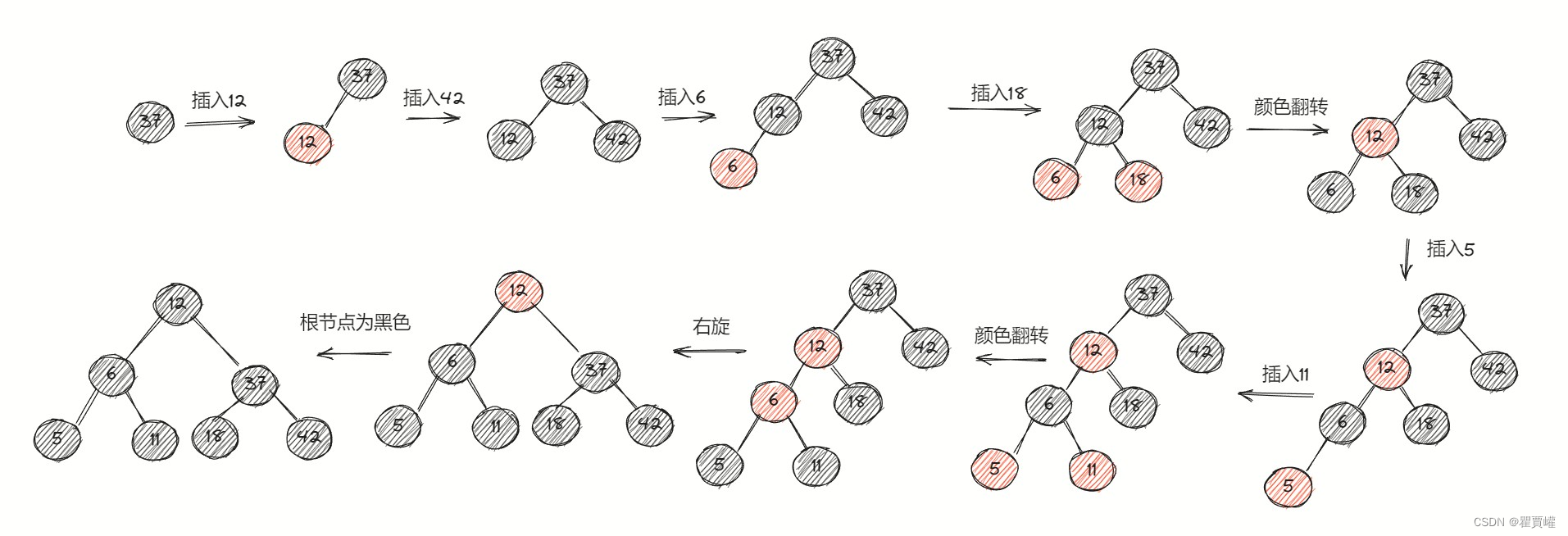
- 插入实例
二三树
二三树与红黑树的性质非常相似,但是二三树能更直观的让人理解构建过程
二三树的性质
二三树是一种自平衡的二叉搜索树,它的特点是每个节点可以存储一个或两个关键字以及相关的子结点链接,它的节点有两种类型
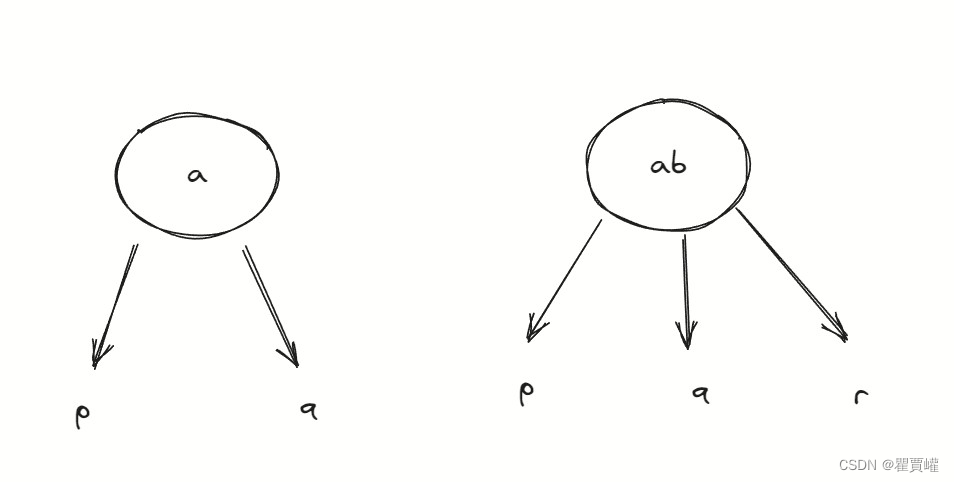
2节点和3节点
- 2节点:包含一个元素和两个子结点,左子节点的所有元素小于该节点,右子节点所有的元素大于该节点
- 3节点:包含两个元素和三个子结点,左子节点的所有元素小于第一个元素,中子节点的所有元素在第一个和第二个元素之间,右子节点的所有元素大于第二个元素
二三树的主要优点是它能保持树的平衡,即所有的叶子节点都在同一层。这使得在二三树中查找、插入和删除操作的时间复杂度都是O(logN),其中N是树中的节点数量。
二三树一个简单的插入例子
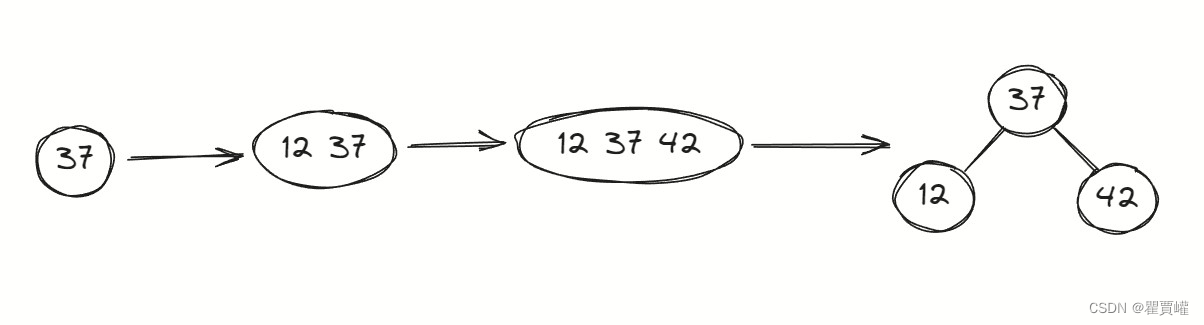
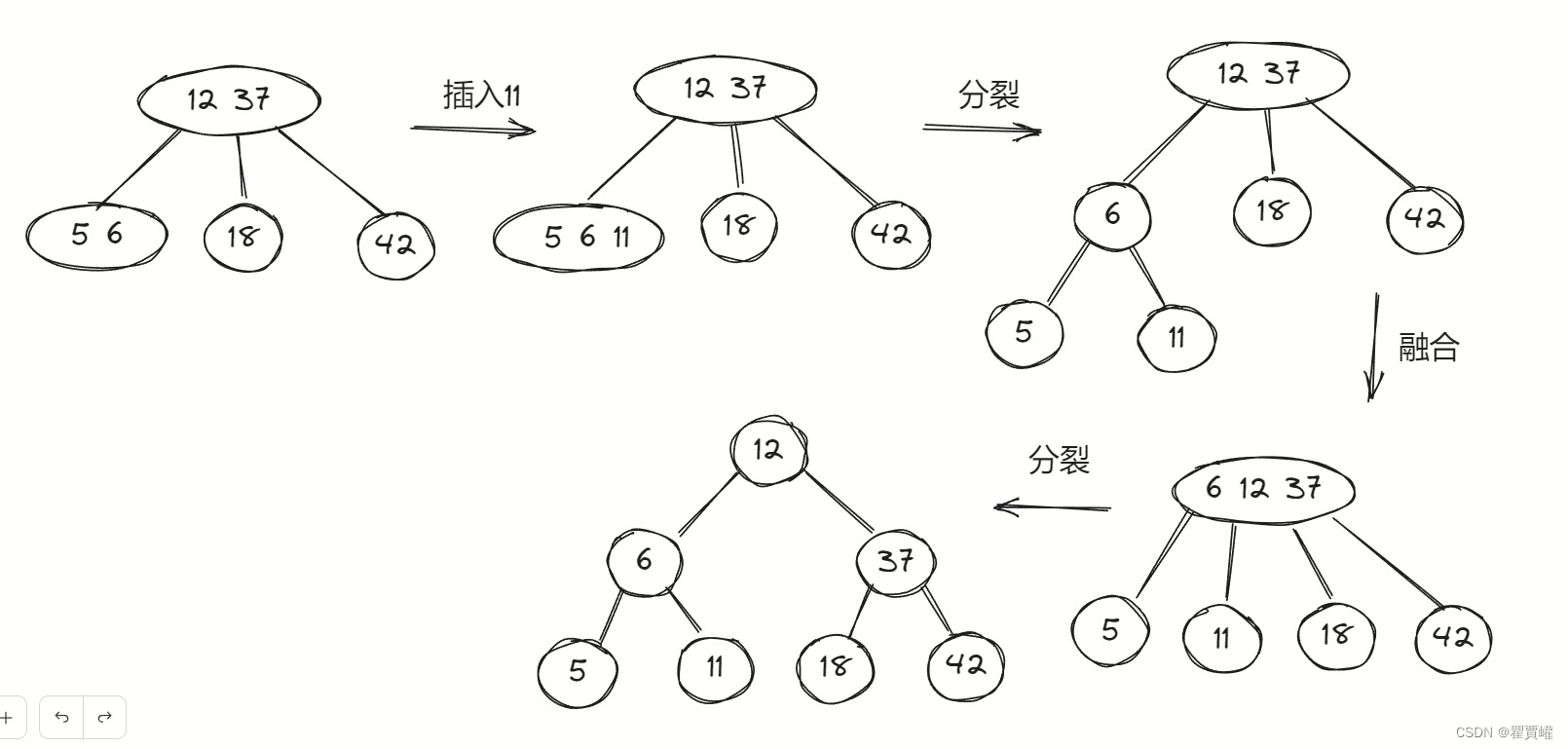
- 如果树是空的,创建一个新的2节点
- 如果树不是空的,找到应该插入的叶子节点
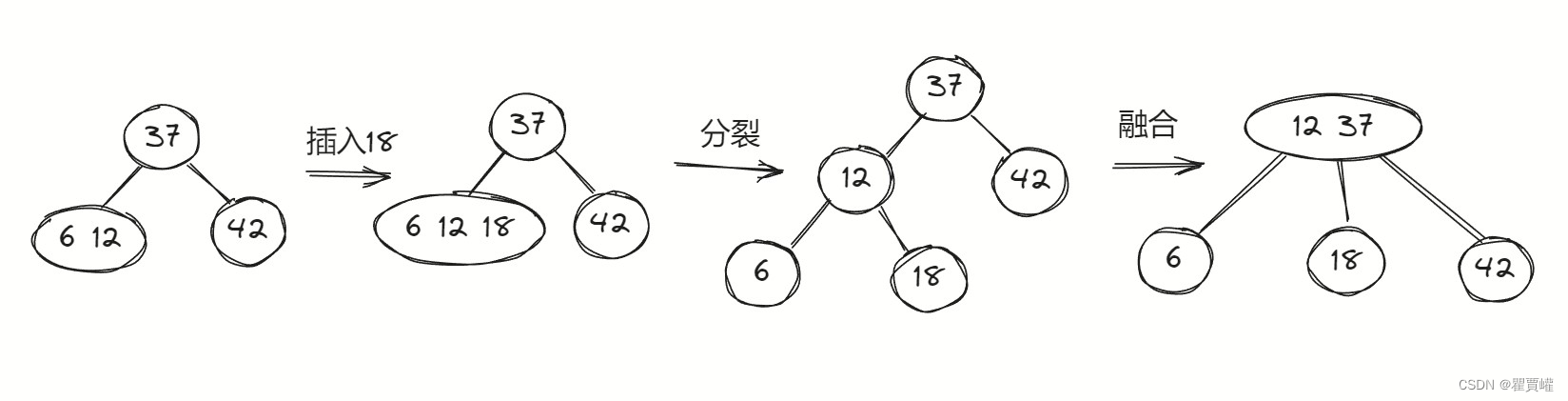
- 如果叶子节点是2节点,插入该节点,使其成为3节点。
- 如果叶子节点是3节点,将该节点的元素一起重新分配到新的节点中,并将中间的元素移动到父节点中。如果父节点也是3节点,就递归地进行这个过程。
二三树的特点
二三树是一棵绝对平衡的树,即从根节点到任意一个叶子节点所经过的节点数都相同。
红黑树
红黑树是一种自平衡的二叉搜索树,它在插入和删除节点时通过重新排列节点来保持树的平衡,从而保证了查找、插入和删除操作的时间复杂度保持在
O(logn)
红黑树的特点
红黑树的节点具有颜色属性,可以是红色或黑色。红黑树满足以下性质:
- 每个节点不是红色就是黑色
- 根节点是黑色的
- 每个叶子节点是黑色的
- 如果一个节点是红色的,那么它的子结点一定是黑色的
- 从一个节点到该节点的子孙节点的所有路径上包含相同数量的黑色节点
红黑树不一定是平衡二叉树,它只是平衡二叉树的一种。但是AVL树由于实现比较复杂,而且插入和删除性能差,在实际环境下的应用不如红黑树
红黑树的实际应用非常广泛,比如Linux内核中的完全公平调度器、高精度计时器、ext3文件系统等等,各种语言的函数库如Java的TreeMap和TreeSet等。
RBTree也是函数式语言中最常用的持久数据结构之一,在计算几何中也有重要作用。值得一提的是,Java 8中HashMap的实现也因为用红黑树取代链表,性能有所提升。
红黑树的节点
相较于AVL树,红黑树的节点中没有节点高度,但是添加了记录节点颜色。
private class Node {
int val;
Node left;
Node right;
Boolean isRed;// 记录节点颜色
public Node(int val) {
this.val = val;
this.left = this.right = null;
this.isRed = true;
}
}
红黑树的插入操作
- 在插入结点时,我们始终认为插入这个结点之前,原来的红黑树是满足红黑树性质的,并且新插入的节点的颜色一定是红色,除了根节点。
- 新增的节点是红色的,这时候如果父亲节点也是红色的这时候就需要维护了。一共可以归纳出三种情况。
// 向树中添加节点
public void add(int val) {
if (contains(val)) {
return;
}
this.root = add(this.root, val);
// 修改根节点颜色
this.root.isRed = false;
}
// 向AVL树中添加节点
private Node add(Node node, int val) {
// 递归到底的情况
if (node == null) {
this.size++;
return new Node(val);
}
// 递归操作
if (node.val > val) {
node.left = add(node.left, val);
} else {
node.right = add(node.right, val);
}
Node resultNode = node;
if (!getNodeColor(node.left) && getNodeColor(node.right)) {
resultNode = leftRotate(resultNode);
}
if (getNodeColor(resultNode.left) && getNodeColor(resultNode.left.left)) {
resultNode = rightRotate(resultNode);
}
if (getNodeColor(resultNode.left) && getNodeColor(resultNode.right)) {
flipColor(resultNode);
}
return resultNode;
}
1. 左旋
在插入节点过程中,如果先插入42再插入37,这时直接就是右边没有问题的结构,但是如果先插入37,再插入42,这时可以看到红色节点出现在了右子树上,这在红黑树中是不允许的,这时候就需要进行左旋。
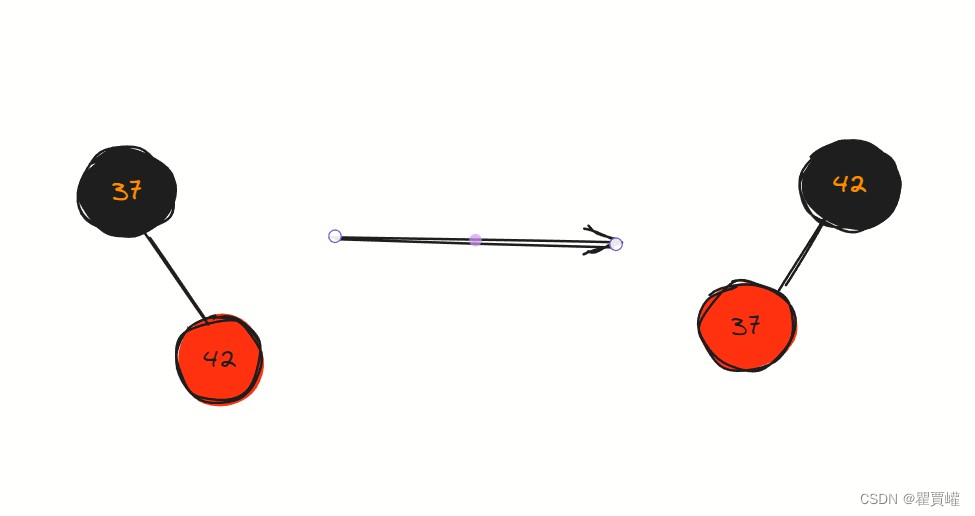
// 左旋转
private Node leftRotate(Node y) {
Node x = y.right;
Node leftX = x.left;
x.left = y;
y.right = leftX;
// 更新颜色
x.isRed = y.isRed;
y.isRed = true;
return x;
}
2. 右旋+颜色翻转
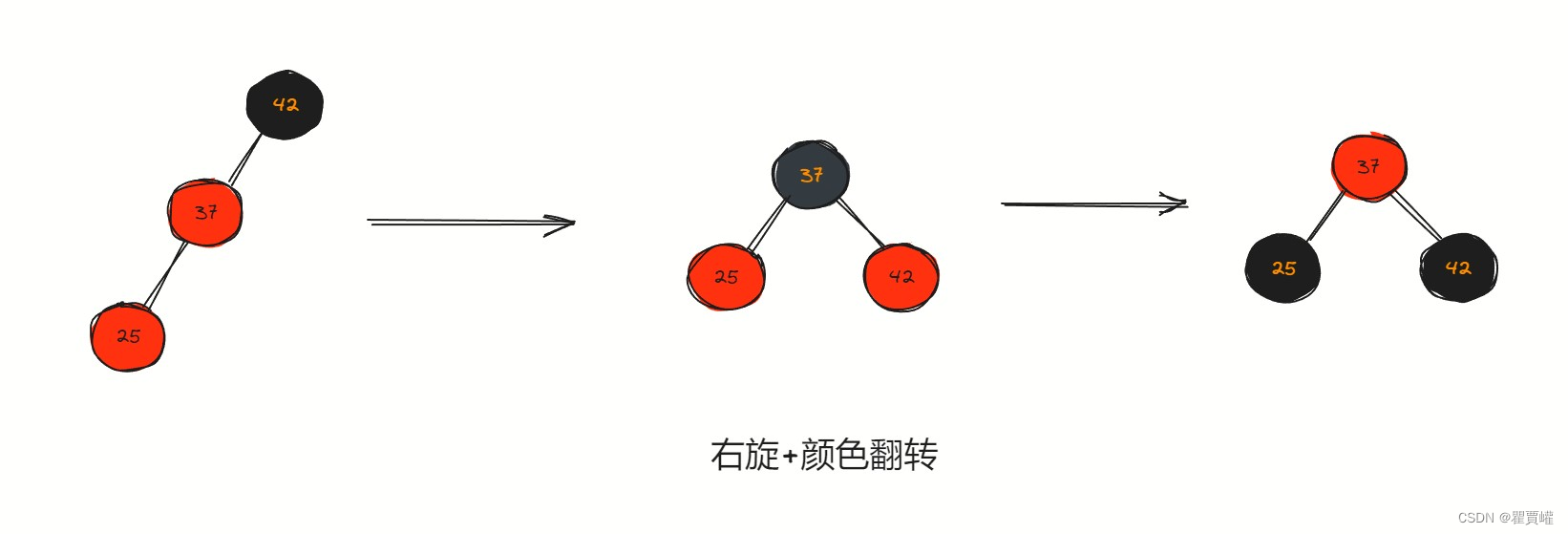
// 右旋转
private Node rightRotate(Node y) {
Node x = y.left;
// 保存x的右子树
Node rightX = x.right;
// 将y作为x的右子树
x.right = y;
y.left = rightX;
// 更新颜色
x.isRed = y.isRed;
y.isRed = true;
return x;
}
// 颜色翻转
private void flipColor(Node node) {
node.isRed = true;
node.left.isRed = false;
node.right.isRed = false;
}
3. 颜色翻转
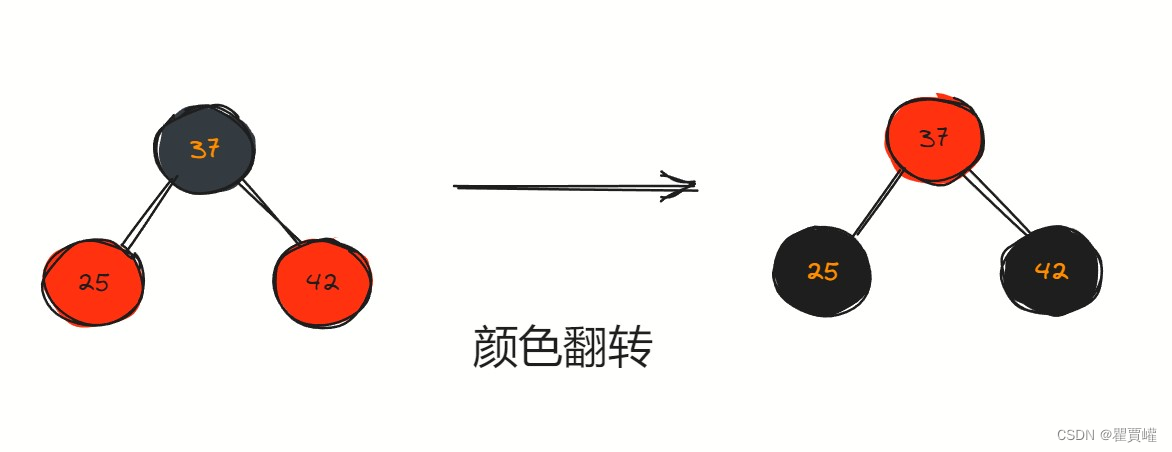
// 颜色翻转
private void flipColor(Node node) {
node.isRed = true;
node.left.isRed = false;
node.right.isRed = false;
}
插入实例