【POJ No. 3764】 最长xor 路径 The xor-longest Path
北大OJ 题目地址
【题意】
在边权树中,路径p的xor长度被定义为路径p上边权的
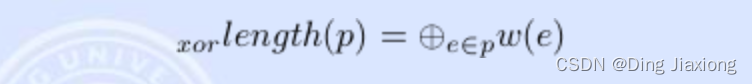
,⊕是xor运算符,表示异或。若一个路径有最大的xor长度,则该路径是xor最长的路径。给定n 个节点的边权树,找到xor最长的路径。
【输入输出】
输入:
输入包含几个测试用例。每个测试用例的第1行都包含一个整数n (1≤n ≤100000),表示节点数。以下n -1行,每行都包含三个整数u 、v 、w (0≤u , v <n ,0≤w <231 ),表示节点u 和v 之间的长度为w 。
输出:
对每个测试用例,都单行输出xor最长的路径长度。
【样例】

【思路分析】
输入样例构建的树如下图所示。
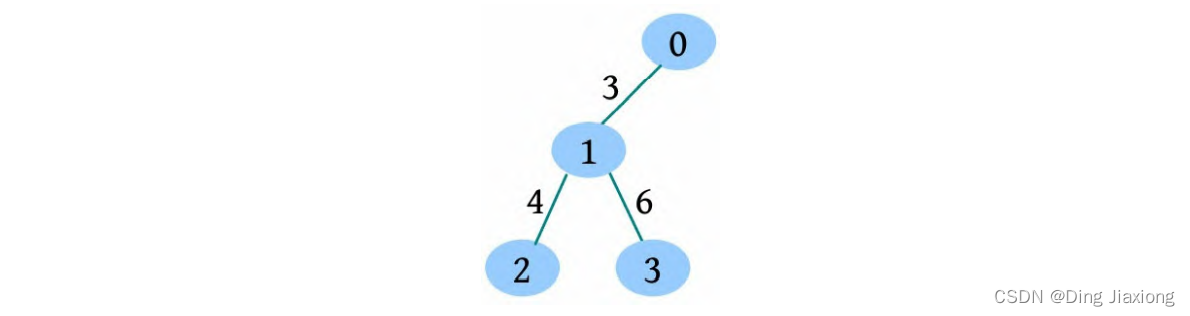
路径0-1-2的xor长度为7(3⊕4=7),是最大的,机内表达为二进制异或运算011⊕100=111。
dx[i ]表示根节点到节点i 路径上所有边权的xor值。通过一次深度优先搜索可以求出所有节点的dx[i ]。树上任意两个节点u 、v 路径上边权的xor值等于dx[u ] xor dx[v ],因为x 和x 异或等于0,所以路径重复的部分会抵消。
问题转变为在dx[1]~dx[n ]中选出两个,求xor的最大值。
考虑问题:给定序列a 1 , a 2 , …, an ,对任意两个数进行xor运算,得到的最大值是多少?可以通过ai 和a 1 , a 2 , …, ai -1 异或,得到一个最大值,枚举i =2, 3, …, n ,取最大值即可。首先将a 1 ,a 2 , …, ai -1 按位插入字典树中,然后沿着与ai 当前位相反的路径走,若与ai 当前位相反的路径不存在,则走ai 当前位。
【算法设计】
① 根据输入数据采用链式前向星存储。
② 深度优先遍历,求解每个节点的dx[i ],即树根到当前节点路径上边权的xor值。
③ 在字典树中查找dx[i ]的异或结果,求最大值,并将dx[i ]插入字典树中。
④ 输出最大值。
【算法实现】
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=100005;
int n,mx;//n个节点,最大值
int trie[maxn*32][2],tot;//字典树存储的是01位
int head[maxn],dx[maxn],cnt;//头结点,从根到当前节点所有边权的xor值
struct Edge{
int to,w,next;
}e[maxn<<1];
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].w=w;
e[cnt].next=head[u];
head[u]=cnt;
}
void dfs(int u,int f){//求dx,从根到当前节点所有边权的xor值
for(int i=head[u];i;i=e[i].next){
int v=e[i].to,w=e[i].w;
if(v==f)//父节点
continue;
dx[v]=dx[u]^w;
dfs(v,u);
}
}
void insert(int num){
int p=1;
for(int i=30;i>=0;i--){
bool k=num&(1<<i);
if(!trie[p][k])
trie[p][k]=++tot;
p=trie[p][k];
}
}
int find(int num){
int p=1,res=0;
for(int i=30;i>=0;i--){
bool k=num&(1<<i);
if(trie[p][k^1]){//走相反路径
res+=1<<i;
p=trie[p][k^1];
}
else
p=trie[p][k];
}
return res;
}
void init(){
memset(head,0,sizeof(head));
memset(trie,0,sizeof(trie));
cnt=0;
tot=1;
mx=0;
}
int main(){
int u,v,w;
while(~scanf("%d",&n)){
init();
for(int i=1;i<n;i++){//n-1条边
scanf("%d%d%d",&u,&v,&w);
add(u+1,v+1,w);
add(v+1,u+1,w);
}
dx[1]=0;
dfs(1,0);
insert(dx[1]);
for(int i=2;i<=n;i++){
mx=max(mx,find(dx[i]));
insert(dx[i]);
}
printf("%d\n",mx);
}
return 0;
}