目录
一、前言
二、PCA的主要参数:
三、数据归约任务1
四、数据规约任务2
一、前言
PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
本质上,通过计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值特征向量,选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中,实现数据特征的降维。 ——来自《知乎》
二、PCA的主要参数:
1)n_components:这个参数指定了希望PCA降维后的特征维度数目。
最常用的做法是直接指定降维到的维度数目,此时n_components是一个大于等于1的整数。
当然,我们也可以指定主成分的方差和所占的最小比例阈值,让PCA类自己去根据样本特征方差来决定降维到的维度数,此时n_components是一个(0,1]之间的浮点数。
2)explained_variance_ratio_,它代表降维后的各主成分的方差值占总方差值的比例,这个比例越大,则越是重要的主成分。
三、数据归约任务1
导入文件“Euro2012_stats.csv”,查看后去除数据中不能直接参与PCA运算的属性列(队伍名称,百分数等列)。
注:对应csv文件可在博客资源中获取。
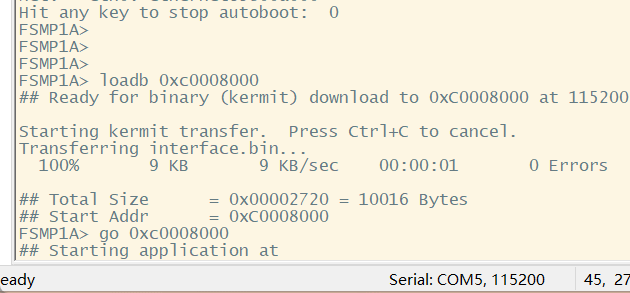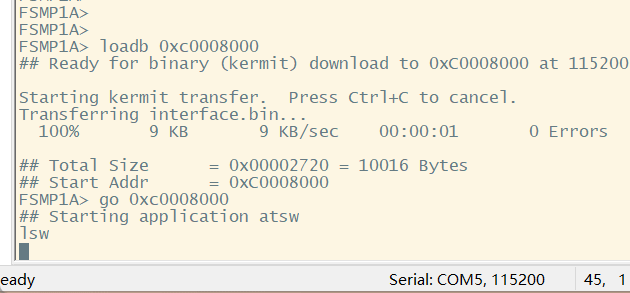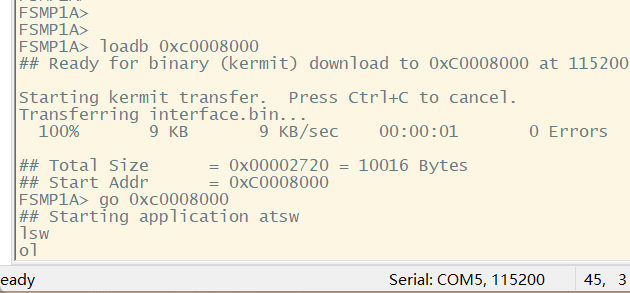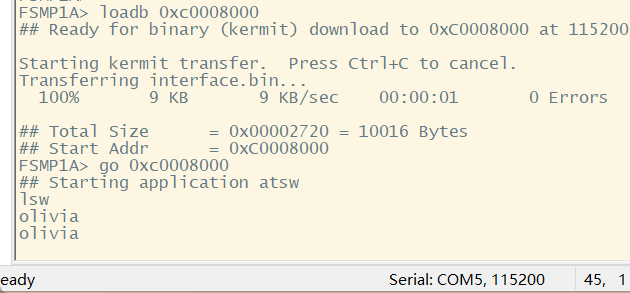
from sklearn.decomposition import PCA
import pandas as pd
eu=pd.read_csv("D:\\dataspace\\Euro2012_stats.csv",encoding="utf-8-sig")
pd.set_option('display.max_rows',None)
pd.set_option('display.max_columns', None)
eu=pd.DataFrame(eu) #数据预览
print(eu.dtypes) #查看各特征列对应的属性
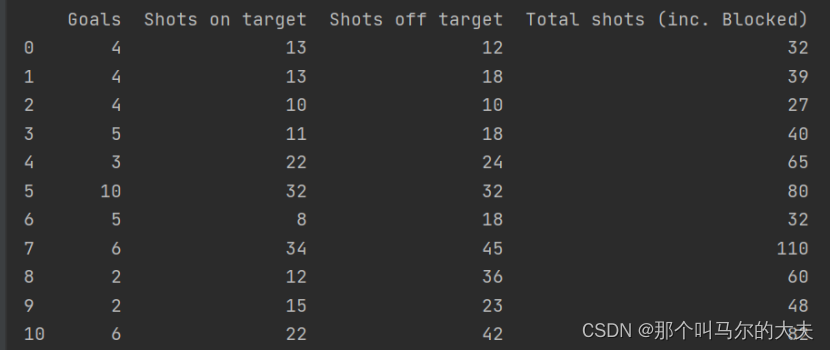
eu1=eu.drop(columns=['Team','Shooting Accuracy','% Goals-to-shots','Passing Accuracy','Saves-to-shots ratio']) #删除非数值型属性的特征列
print(eu1) #删除后的数据预览数据预览:
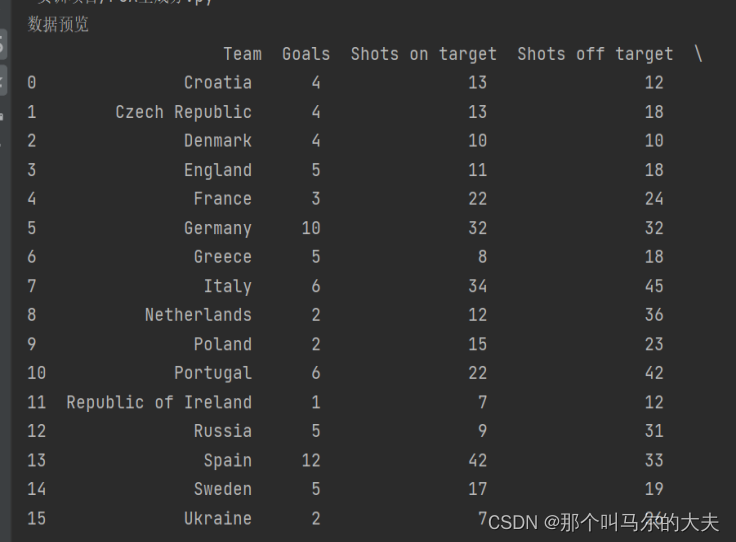
查询各特征对应的属性:

删除后的数据预览:
四、数据规约任务2
对数据进行PCA分析。引入pca(from sklearn.decomposition import PCA),将所有数值型属性列降维降到5维,并查看降维结果与信息。通过分析结果,选择并说明合适的压缩维度。(自学explained_variance_ratio_,在实验报告中说明数值代表什么含义,并展示结果)
from sklearn.decomposition import PCA
pca=PCA(n_components=5)
pca.fit(eu1)
newdata=pca.transform(eu1)
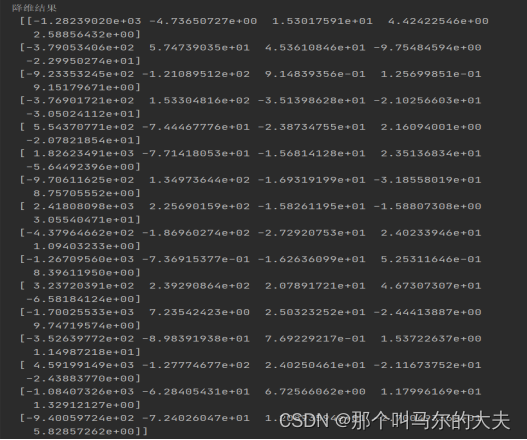
print('降维结果\n',newdata)
newdata1=pd.DataFrame(newdata)
print('方差值所占比\n',pca.explained_variance_ratio_)降维结果如下图:

通过计算explained_variance_ratio_可以得到各主成分的方差值占总方差值的比例,也就是方差贡献率。
将降维后的数据特征列的首列作为y轴,原数据中的team列作为x轴,绘制折线图:
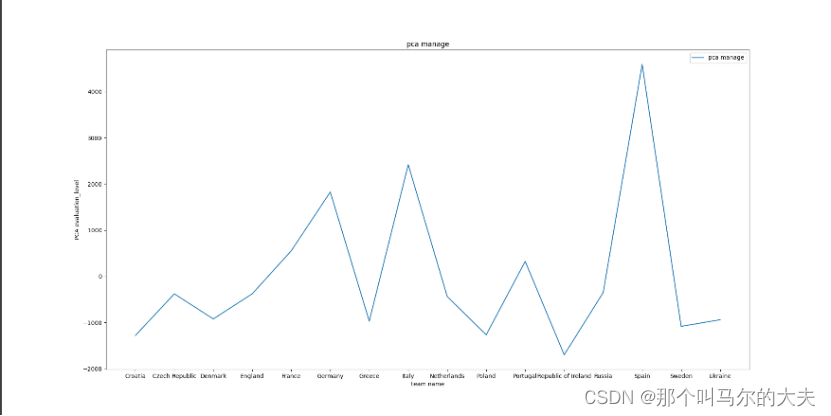
重新调参,确定合适的压缩维度:
scorelist =[]
for i in range(16):
pca1=PCA(n_components=i)
pca2=pca1.fit(eu1)
score=pca2.score(eu1)
scorelist.append(score)
print(scorelist)
import matplotlib.pyplot as plt
plt.figure(figsize=(20,10))
plt.plot(range(16),scorelist,label='score')
plt.legend()
plt.show() 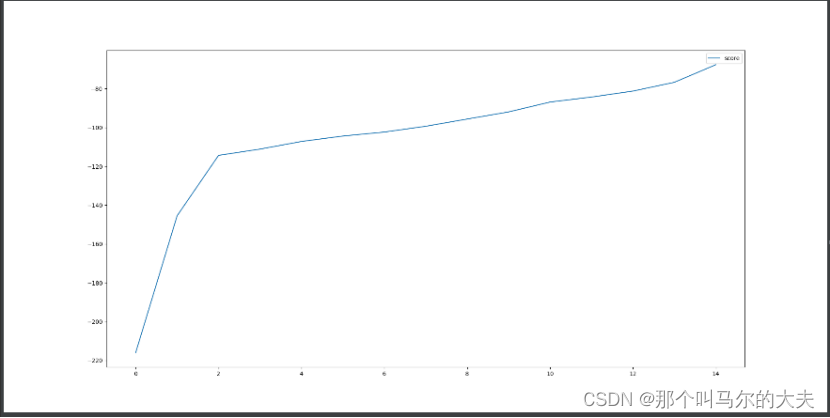
如图,根据score的值可得出,最高点对应横坐标为16,但总共数据对象就16簇,划分太多容易造成分类不准确的情况,故适合划分的压缩维度为8簇更合适。





![【洛谷】P1073 [NOIP2009 提高组] 最优贸易(dp+搜索)](https://img-blog.csdnimg.cn/8bf8054b1da64e2c8f86c1eeb2ed7680.png)