作者在前面的文章中介绍了粒子群算法的原理及其2种改进算法，本文将基于这三种优化方法，应用于支持向量机进行预测，并对比改进算法与标准粒子群算法的预测性能，结果显示改进后的方法能够得到更佳的预测效果。

00 文章目录

1 支持向量机
2 粒子群优化算法及其改进
3 支持向量机预测模型建立
4 代码目录
5 仿真
6 源码获取

01 支持向量机

支持向量机（Support Vector Machine, SVM）是由前苏联教授Vapnik最早提出的。支持向量机是一种新型机器学习算法，其基本思想把原有数据训练集映射到高维特征空间，借助损失函数和惩罚因子，从而达到精确度和计算复杂度相平衡，因此，可以将上述问题看作一个在高纬度的二次回归问题来进行求解，其函数表达式为：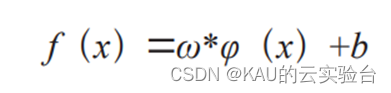

其中，ω 为超平面权重向量，b是SVM模型的参数，φ( x) 表示 x 的映射变换。根据文献得到回归支持向量机可以表示为：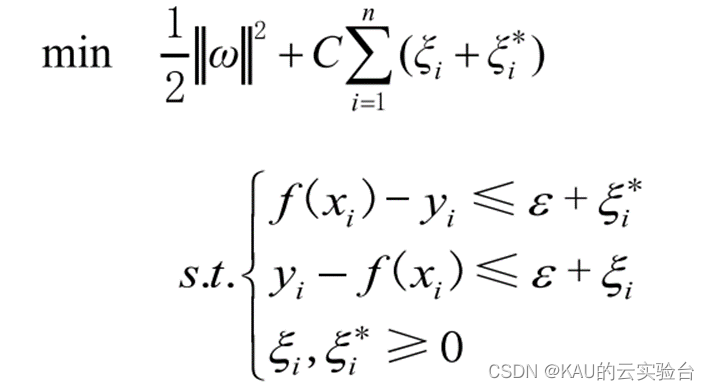

其中，ξ_i,ξ_i^*是松弛变量 C，是正实数松弛惩罚因子
非线性回归求解中，可以使用核函数 K(xi,xj)=φ(xi)·φ(xj)把所需要的训练集映射到高维空间，从而就可以将其 变化到线性问题的拟合，可得到一样的效果，非线性拟合函数为：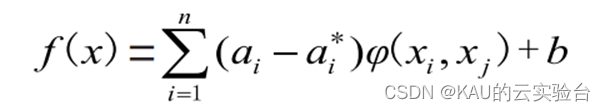

则将问题转化为对偶求解：

其中，ni,ni*,ai,ai*为拉格朗日乘子，b为阈值。由于高斯径向基核函数拥有处理样本输入与输出之间复杂非线性关系的良好能力，而且参数选取少，计算效率高，因此采用效果更好的RBF为核函数。
惩罚系数 C 和RBF核系数 g 对SVM的性能有重要影响。其中，惩罚系数 C 是模型对误差的容忍度，数值越大，容忍度越差；数值越低，欠拟合越容易; 核系数g的选取对支持向量机的学习能力和预测精度有很大的影响。通常这些参数是通过人工设定，但常会导致拟合的数据出现较大偏差，因此用优化算法对参数进行寻优是必要的。
将SVM应用于拟合回归即为SVR(support vector regression)

02 粒子群优化算法及其改进

粒子群算法及其实现
自适应混沌粒子群算法及其实现
量子粒子群算法及其实现

03 支持向量机预测模型建立

本文使用作者提到的2种改进的粒子群算法来快速寻优到最佳惩罚参数和核函数参数，并与标准粒子群算法进行对比，以c和g的取值作为粒子群的位置参数，用上述的两种改进方法以及标准粒子群算法按照其流程进行迭代寻优。
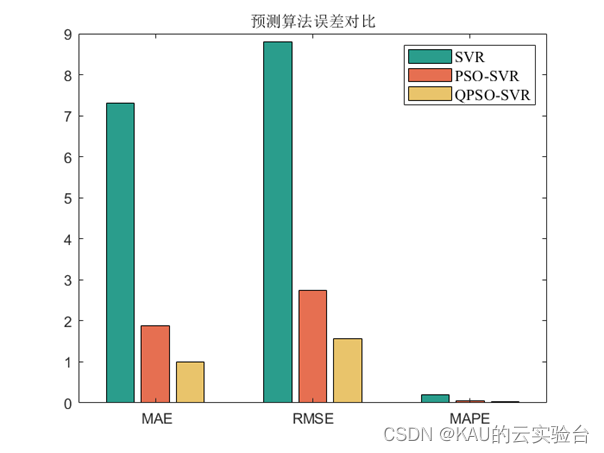
预测完成后，为了验证所建模型的准确性和精度，分别采用均方根差(Root Mean Square Error，RMSE) 、平均绝对百分误差( Mean Absolute Percentage Error，MAPE) 和平均绝对值误差 ( Mean Absolute Error，MAE) 作为评价标准。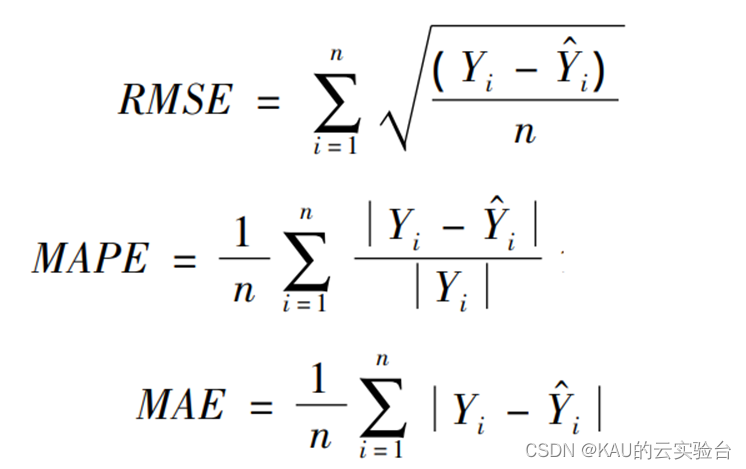

式中 Yi 和Y ^ i分别为真实值和预测值; n 为样本数。

04 代码目录

三种算法文件如下：

IPSO-SVR:
包含libsvm工具包，以及自适应混沌粒子群和标准粒子群算法。

main_ipso.m部分源码如下：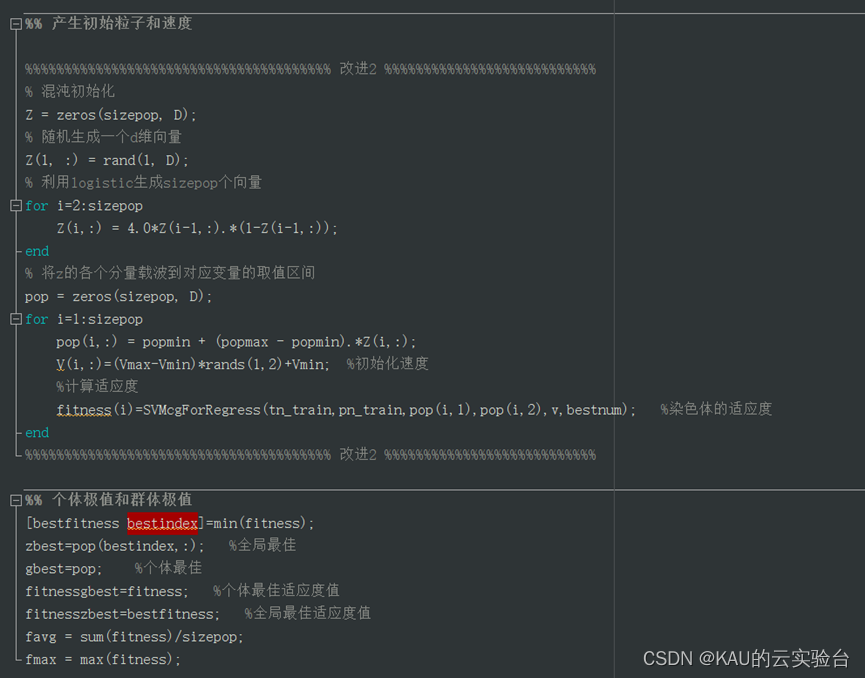

PSOSVR:
包含libsvm工具包，以及标准粒子群算法。

main_pso.m部分源码如下：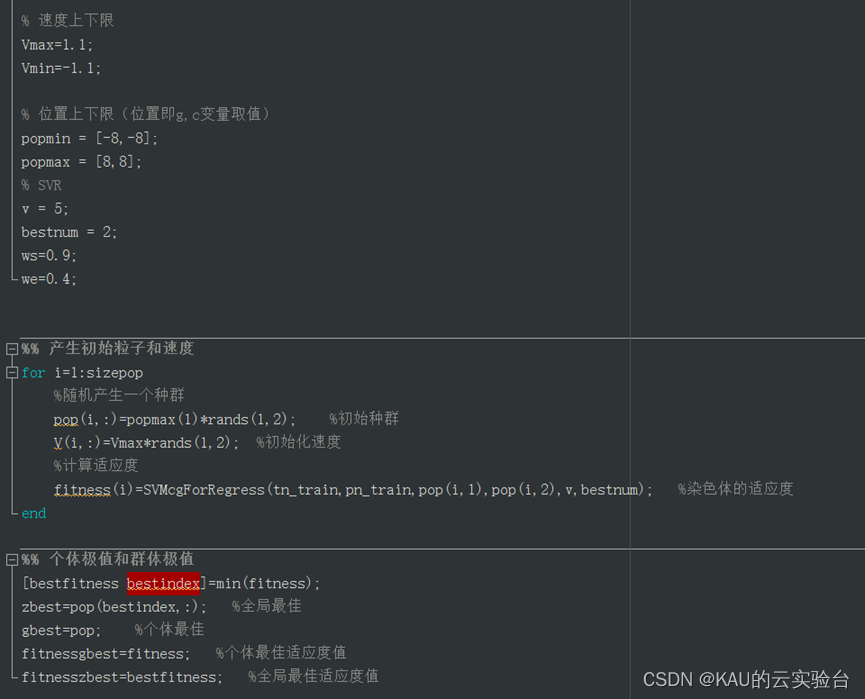

QPSO-SVR:
包含libsvm工具包，以及量子粒子群和标准粒子群算法。

main_qpso.m部分源码如下：

05 仿真

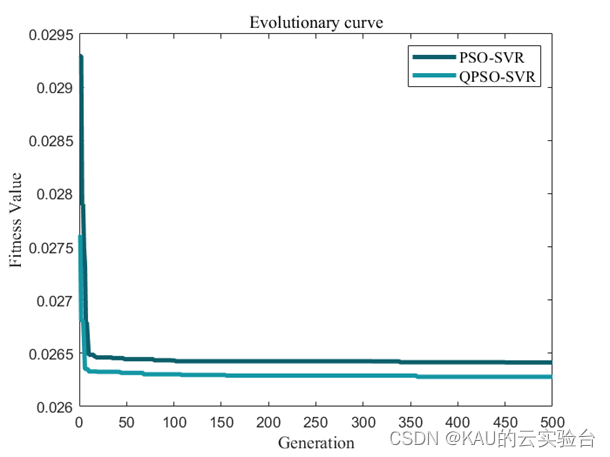
由于量子粒子群与自适应混沌粒子群的改进方向大相径庭，量子粒子群省去了粒子群大部分的控制参数，调参简单，而自适应混沌粒子群则将粒子群的控制参数进一步非线性化，因此对于不同的应用问题必然有其不同的优势，故不将这两个算法一起比较，而是分开比较。
这里展示量子粒子群

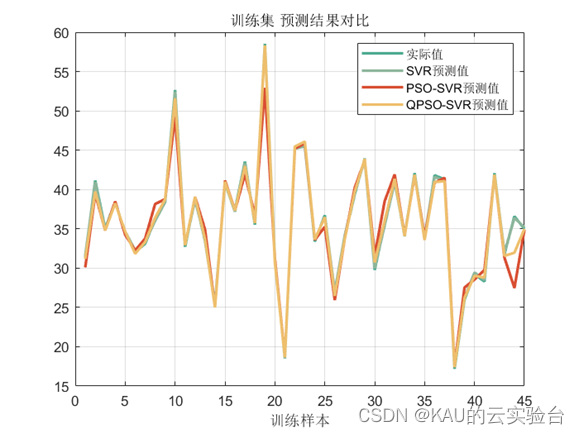
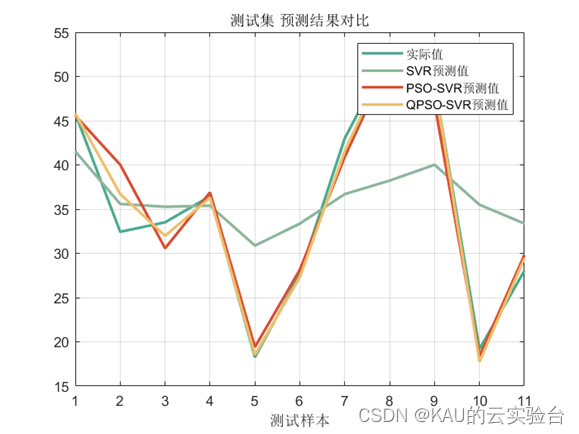
06 源码获取

PSO-SVR：
在关注作者微信公众号： KAU的云实验台 
后台回复：             PSOSVR            即可（大写字母）

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
IPSO-SVR：
https://mbd.pub/o/bread/ZJuTk5lp

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
QPSO-SVR：
https://mbd.pub/o/bread/mbd-ZJuTk5lq

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

如果这篇文章对你有帮助或启发，可以点击右下角的赞 (ง •̀_•́)ง(不点也行)，若有定制需求，可私信作者。