文章目录
- 1005.K次取反后最大化的数组和
- 思路
- 直接升序排序的写法
- 最开始的写法:逻辑错误
- 修改版
- 时间复杂度
- 自定义sort对绝对值排序的写法
- sort的自定义比较函数cmp必须声明为static的原因
- std::sort升降序的问题(默认升序)
- 时间复杂度
- 总结
- 134.加油站
- 思路
- 完整版
- 总结
1005.K次取反后最大化的数组和
- 本题重点是逻辑问题,同时复习static和sort的自定义操作与时间复杂度
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
- 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。
以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
输入:nums = [4,2,3], k = 1
输出:5
解释:选择下标 1 ,nums 变为 [4,-2,3] 。
示例 2:
输入:nums = [3,-1,0,2], k = 3
输出:6
解释:选择下标 (1, 2, 2) ,nums 变为 [3,1,0,2] 。
示例 3:
输入:nums = [2,-3,-1,5,-4], k = 2
输出:13
解释:选择下标 (1, 4) ,nums 变为 [2,3,-1,5,4] 。
提示:
1 <= nums.length <= 10^4-100 <= nums[i] <= 1001 <= k <= 10^4
思路
本题主要含义是,给出一个数组,基于这个数组在任意可重复的下标做k次取反,计算k次取反后的最大和。
首先,数组内有正数和负数,我们优先对负数进行取反。在负数里,我们又要优先对绝对值最大的负数进行取反。
当负数全部取反,数组里全部是正数之后,此时次数还没有用完,我们需要再优先对绝对值最小的正数取反。
局部最优就是,优先找绝对值最大的负数/绝对值最小的正数取反。全局最优就是最后的数组和最大。
本题实际上涉及到了两次贪心。一次是数组有正有负,一次是数组里全是正数。
直接升序排序的写法
- 第一步:全部转成正数
- 第二步:全转成正数之后重新排序,因为转成正数之后还有可能出现比现有正数更小的正数!
最开始的写法:逻辑错误
class Solution {
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
//先对数组进行排序,这里可以考虑自定义比较函数,按照绝对值的大小进行排序,也可以直接升序排序
sort(nums.begin(),nums.end());
int sum=0;
for(int i=0;i<nums.size();i++){
//cout<<nums[i]<<endl;
if(nums[i]<0&&k>0){
nums[i]=-nums[i];
//cout<<nums[i]<<endl;
k--;
continue;
}
if(nums[i]>=0&&k>0){
while(k>0){
nums[i]=-nums[i];
cout<<nums[i]<<endl;
k--;
}
}
//if(k==0) break;
}
for(int i=0;i<nums.size();i++){
//cout<<nums[i]<<endl;
sum += nums[i];
}
return sum;
}
};
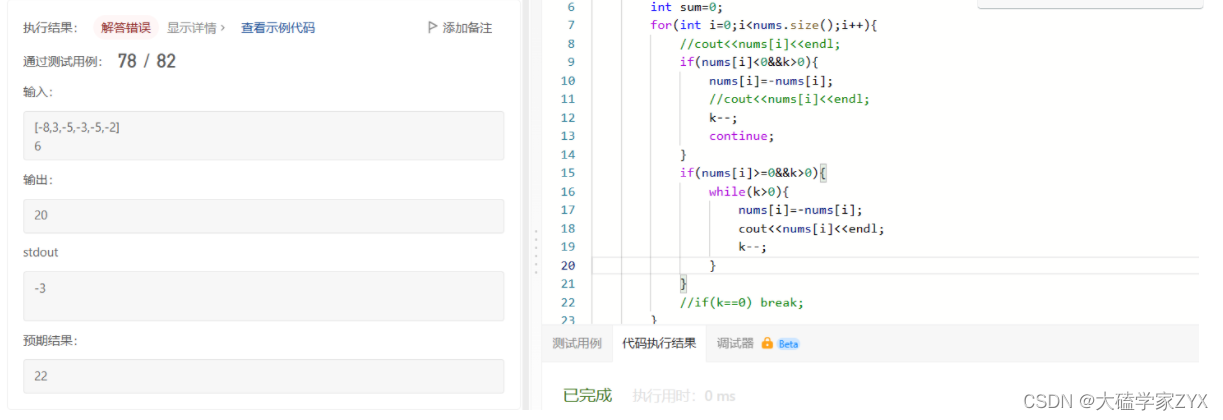
这种写法出现了逻辑错误,原因是出现了如下案例:

本题中需要在最小的正数上面消耗次数,而不是把所有的负数转正数之后,在原排序基础上消耗原有的正数!
修改版
- 这种写法需要排序两次,因为负数全转成正数之后,很有可能出现更小的正数
class Solution {
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
//先对数组进行排序,这里可以考虑自定义比较函数,按照绝对值的大小进行排序,也可以直接升序排序
sort(nums.begin(),nums.end());
int sum=0;
//先把所有负数转成正数
for(int i=0;i<nums.size();i++){
//cout<<nums[i]<<endl;
if(nums[i]<0&&k>0){
nums[i]=-nums[i];
//cout<<nums[i]<<endl;
k--;
}
}
//再重新排序,并在重排后的第一个元素上消耗剩余所有次数
sort(nums.begin(),nums.end());
while(k>0){
nums[0]=-nums[0];
k--;
}
//求和
for(int i=0;i<nums.size();i++){
cout<<nums[i]<<endl;
sum += nums[i];
}
return sum;
}
};
时间复杂度
这种写法需要排序两次,时间复杂度主要取决于sort的复杂度。
在C++中,sort函数的时间复杂度是O(nlogn),其中n是数组的长度。因此,上述代码的时间复杂度是O(nlogn)(对原数组排序)+ O(n)(遍历数组对负数进行操作)+ O(nlogn)(再次对数组排序)+ O(n)(对剩余的k进行处理和求和)= O(nlogn)。
实际上,时间复杂度为O(nlogn + nk),先进行了一次全体元素的排序(O(nlogn)),然后可能对每个元素进行多次操作(O(nk))。
排序次数过多导致开销会增大。此时我们考虑优化。
自定义sort对绝对值排序的写法
- 这种写法,我们在一开始,就对元素绝对值进行排序。
- 注意绝对值排序一定要降序排序!因为我们要先消耗数值大的负数!sort本身是升序,只用sort的话数值大的负数会在前面,但是这里自定义了绝对值,就必须把数值大的放在前面,用**greater(降序)**来实现!
class Solution {
public:
int sum=0;
static bool cmp(int a,int b){
if(abs(a)>abs(b))
return true;//绝对值降序排序,因为要先处理大的负数
else
return false;
}
int largestSumAfterKNegations(vector<int>& nums, int k) {
sort(nums.begin(),nums.end(),cmp);//绝对值降序排序
for(int i=0;i<nums.size();i++){
//第一次遍历的时候,只在负数上消耗次数!
if(nums[i]<0&&k>0){
nums[i]=-nums[i];
k--;
}
if(k==0) break;
}
//如果此时还有k没消耗完,看看k是奇数or偶数,如果是偶数就不用管了
if(k%2==1){
//如果是奇数,直接最小值取反就是结果
nums[nums.size()-1]= - nums[nums.size()-1];
}
for(int i:nums){//遍历Nums
sum+=i; //这种写法,i就是元素本身,不能写成nums[i]否则会越界
}
return sum;
}
};
sort的自定义比较函数cmp必须声明为static的原因
c++静态变量成员函数和全局函数的区别_成员函数全局函数_大磕学家ZYX的博客-CSDN博客
cmp函数被声明为static,这是因为std::sort需要一个能够在全局访问的函数,或者一个lambda函数。
如果cmp不是static的,那么这就意味着它需要一个对象上下文(因为非静态成员函数都有一个隐含的this指针参数)。然而在这种情况下,我们不能给出这样一个上下文。所以,我们需要使cmp函数成为一个静态成员函数,这样它就可以在没有对象上下文的情况下被调用。
static的用法补充:static在 C++ 中的四种用法_大磕学家ZYX的博客-CSDN博客
std::sort升降序的问题(默认升序)
注意,在C++中,std::sort函数默认的排序方式是从小到大,也就是升序排序。这个函数会对输入范围内的元素进行排序,使得排序后的元素序列是非递减的。
如果要实现降序排序,你可以给std::sort函数提供第三个参数,即一个自定义的比较函数或者lambda表达式。这个比较函数定义了两个元素的比较规则。
例如,如果想对candidates数组进行降序排序,你可以这样做:
std::sort(candidates.begin(), candidates.end(), std::greater<int>());
在这个代码中,std::greater<int>()是一个函数对象,它定义了一个规则,使得sort函数会按照这个规则进行排序,也就是降序排序。
另一种方式是使用lambda表达式来定义比较规则:
std::sort(candidates.begin(), candidates.end(), [](int a, int b) {return a > b;});
在这个代码中,[](int a, int b) {return a > b;}是一个lambda表达式,它接受两个参数a和b,如果a > b,则返回true,这样sort函数就会按照这个规则进行降序排序。
时间复杂度
优化写法时间复杂度同样主要取决于排序的复杂度,即O(nlogn)。遍历数组进行操作的时间复杂度是O(n)。所以总的时间复杂度是O(nlogn)。
总结
第二种写法的优化主要体现在两个地方:
- 通过使用绝对值的大小进行排序,可以优先处理绝对值大的元素。这样,不仅可以减少不必要的符号反转操作,而且可以更好地利用操作次数,因为对绝对值大的元素进行反转,可以获得更大的结果。
- 通过在第一次遍历中只在负数上消耗次数,并在处理完所有负数后,不需要再次进行排序,因为此时已经是从小到大的正数顺序(本来就是绝对值排序)。再根据剩余次数的奇偶性进行相应操作,可以避免对每个元素进行多次操作,进一步降低时间复杂度。
- sort升序的写法和绝对值降序的写法如下图所示。局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大。

134.加油站
- 本题可以和 53.最大子数组和 放在一起来看,都是属于遇到了不需要的结果,直接统计量清零,重新开始算起点的类型。
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
提示:
gas.length == ncost.length == n1 <= n <= 10^50 <= gas[i], cost[i] <= 10^4
思路
本题是模拟加油站跑圈的过程,每到一个站点补充油,开到下一个站点消耗油。需要让目前的油+补充油高于消耗油,才能开到下一个站点。大致情况如图:

本题的暴力解法是两个for循环,一个循环模拟每个站点作为起始位置的情况,一个循环看这个位置能不能跑一圈,时间复杂度就是n^2。暴力解思路简单,但是跑一圈的过程不太好做。while模拟转圈过程比较复杂!
本题最好还是贪心的思路来解。本题有补充+消耗,我们要看的就是对油箱是增加作用还是消耗作用。也就是统计净增长量。如下图所示。
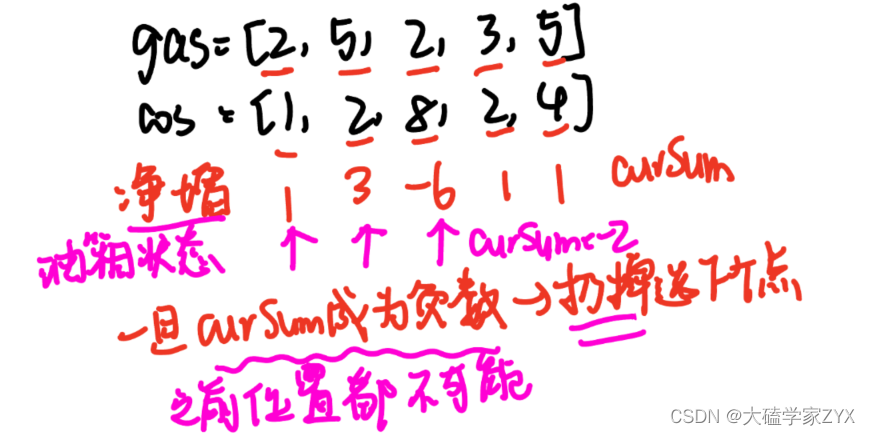
我们用curSum变量去累积每个站点油箱的状态。
一旦油箱在这个站点状态成为负数,说明从这个位置之前的任意位置开始,都不可能到达终点!此时我们直接选择负数状态位置的i+1作为新的起始点,之前的起始点就全部抛弃掉。
遇到i位置的curSum<0,就直接让i+1作为起点,这种逻辑是否正确可以画图来看:
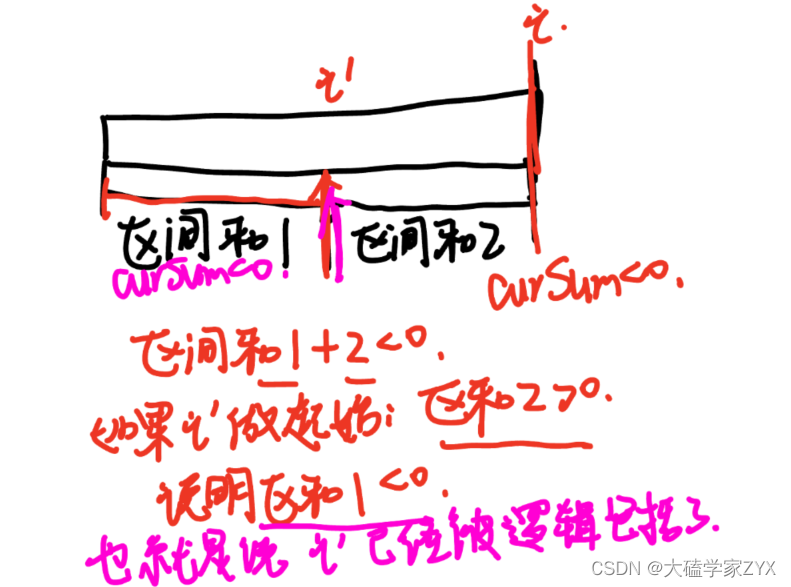
贪心的思路就是不断累加curSum,局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。
局部最优可以推出全局最优并且想不出来反例,反例在上图有大概的证明,因此可以尝试贪心。
完整版
- 和 53.最大子数组和 一样,本题同样也不需要改变for的遍历方式!startIndex只是用来记录位置方便返回,实际上重新开始遍历的时候,只需要把统计量curSum置零就可以了!
- 净增长量如果<0,说明此时油箱状态成了负数,也就是说在此位置之前的点,都不可能跑完一圈;此时应重新置零,开始统计新的净增长,直到净增长量不是0,才说明能够跑完一圈
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int curSum=0;
int totalSum=0;//统计所有的rest,看是不是全是负数,全是负数说明不可能跑完一圈
for(int i=0;i<gas.size();i++){
totalSum+=(gas[i]-cost[i]);
}
//如果净增长到最后都是负数,返回-1
if(totalSum<0) return -1;
int startIndex=0;//记录i+1作为起始位置,找到合适的起始i
for(int i=0;i<gas.size();i++){
curSum += (gas[i]-cost[i]);//统计剩余油量
if(curSum<0){//i之前的油量rest累加为负数
startIndex=i+1;
curSum=0;//重新置零,开始统计新的净增长,直到最后净增长量不是0,才说明能够跑完一圈
}
}
return startIndex;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
总结
贪心的主要策略就是局部最优可以推出全局最优,进而求得起始位置。本题和 53.最大子数组和 都属于遇到了不需要结果,直接重置统计量,相当于重置起点的类型。