上一小节对神经网络有了基本的了解，这一小节就看一下如何用代码来实现一个神经网络。
我们所用的案例还是那个温度转换的案例，只不过需要我们把之前的线性模型替换成神经网络模型，并重新训练以找到适合神经网络的权重。
依照我们的经验，前面有一些前置步骤，一部分大部分代码我们都学过了，包括了引用相关的包，设置notebook的显示规范，初始化数据，分割训练集和验证集以及对数据进行标准化。

使用nn模块

%matplotlib inline
import numpy as np
import torch
import torch.optim as optim

torch.set_printoptions(edgeitems=2, linewidth=75)

t_c = [0.5,  14.0, 15.0, 28.0, 11.0,  8.0,  3.0, -4.0,  6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1) #这个地方跟之前有些区别，我们给数据进行了升维，目的是把数据转化成单个的样本，如果这里不太明白不要紧，后面会讲
t_u = torch.tensor(t_u).unsqueeze(1) 

t_u.shape
outs:
torch.Size([11, 1])

n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)

shuffled_indices = torch.randperm(n_samples)

train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]

train_indices, val_indices
outs:
(tensor([5, 6, 1, 4, 9, 0, 3, 2, 8]), tensor([ 7, 10]))
#训练集数据获取
t_u_train = t_u[train_indices]
t_c_train = t_c[train_indices]
#验证集数据获取
t_u_val = t_u[val_indices]
t_c_val = t_c[val_indices]

# 某种很简单的数据标准化
t_un_train = 0.1 * t_u_train
t_un_val = 0.1 * t_u_val

在PyTorch中，提供了一个torch.nn模块，里面提供了各种创建神经网络的功能。

#加载nn模块
import torch.nn as nn

linear_model = nn.Linear(1, 1) # 这里我们使用的仍然是nn模块里面的线性模型，传入的参数1,1分别为输入tensor的大小和输出tensor的大小，还有一个默认的参数‘带有偏置’
linear_model(t_un_val)#调用模型
outs:tensor([[2.4104],
        [5.8570]], grad_fn=<AddmmBackward0>)

这里用到的linear模型和我们以前自己构建的线性模型并没有什么区别，可以输出此时的权重和偏置看一下

linear_model.weight
Parameter containing:
tensor([[0.1007]], requires_grad=True)

linear_model.bias
Parameter containing:
tensor([-0.6234], requires_grad=True)

批量训练

前面我们看到了如何做好一个调包侠，使用nn模块里面的模型来进行训练。
如我们前面说的，我们可以以batch的形式来训练模型，PyTorch里的nn.Module及其子类也都设计好了，可以同时接收多个样本。批量输入样本有利于最大化利用计算资源。

在我们传入参数的时候，模块期望输入的第0维是每个批次的样本数量。

比如像下面这样

x = torch.ones(10, 1) #初始化10 * 1 tensor，表示10个样本，每个样本尺寸是1
linear_model(x)
outs:
tensor([[0.6814],
        [0.6814],
        [0.6814],
        [0.6814],
        [0.6814],
        [0.6814],
        [0.6814],
        [0.6814],
        [0.6814],
        [0.6814]], grad_fn=<AddmmBackward>)

从上面初始化的数据，我们从模型得到的结果都是一样的，如果像我们前面搞图像的输入时候，每个批次三张图像，那么我们初始化的数据应该就是一个3 * 3 * 256 * 256的tensor。

就像我们开头的代码里缩写的

t_c = torch.tensor(t_c).unsqueeze(1)

我们用了unsqueeze方法给数据进行升维，升维完成之后就成了一个11 * 1的tensor。
接下来我们继续构建训练步骤，加入优化器。

optimizer = optim.SGD(
    linear_model.parameters(), # 这里我们又省了一步，原来是自己攒了一个params，现在也不需要了，直接调用方法
    lr=1e-2)

list(linear_model.parameters()) #查看当前参数
outs:
[Parameter containing:
 tensor([[0.1007]], requires_grad=True), Parameter containing:
 tensor([-0.6234], requires_grad=True)]

写成一个完整的循环

#传入的参数：迭代次数，优化器，模型，损失函数，训练特征数据，验证特征数据，训练结果数据，验证结果数据
def training_loop(n_epochs, optimizer, model, loss_fn, t_u_train, t_u_val,
                  t_c_train, t_c_val): #这里注意，直接定义了一个model参数，把模型作为参数传入，因此我们可以替换不同的模型
    for epoch in range(1, n_epochs + 1):
        t_p_train = model(t_u_train)  #训练
        loss_train = loss_fn(t_p_train, t_c_train)

        t_p_val = model(t_u_val) #验证
        loss_val = loss_fn(t_p_val, t_c_val)
        
        optimizer.zero_grad() #梯度归零，防止上一轮迭代的梯度数据混入
        loss_train.backward() #反向传播
        optimizer.step() #优化器迭代参数

        if epoch == 1 or epoch % 1000 == 0: #第一轮训练或者每1000轮训练输出一次结果
            print(f"Epoch {epoch}, Training loss {loss_train.item():.4f},"
                  f" Validation loss {loss_val.item():.4f}")

接下来就开始训练了

def loss_fn(t_p, t_c):
    squared_diffs = (t_p - t_c)**2
    return squared_diffs.mean()

linear_model = nn.Linear(1, 1) 
optimizer = optim.SGD(linear_model.parameters(), lr=1e-2)

training_loop(
    n_epochs = 3000, 
    optimizer = optimizer,
    model = linear_model,
    loss_fn = loss_fn,
    t_u_train = t_un_train,
    t_u_val = t_un_val, 
    t_c_train = t_c_train,
    t_c_val = t_c_val)

print()
print(linear_model.weight)
print(linear_model.bias)

outs:
Epoch 1, Training loss 244.1249, Validation loss 78.6624
Epoch 1000, Training loss 4.5626, Validation loss 2.7117
Epoch 2000, Training loss 2.8499, Validation loss 3.3772
Epoch 3000, Training loss 2.7084, Validation loss 4.6429

Parameter containing:
tensor([[5.5946]], requires_grad=True)
Parameter containing:
tensor([-18.4819], requires_grad=True)

神经网络

看到这里，怎么搞来搞去还是一个线性模型，怎么还没有出现神经网络，到底在搞什么？快把它搞成一个神经网络！

要搞成神经网络，像我们前一节讲的，似乎已经很简单了，就是在线性单元的后面再叠加一个激活函数单元。PyTorch提供了一个nn.Sequential来连接模型，下面的代码中组合了三个单元，第一个线性单元输入tensor大小为1，输出tensor大小13，后面接一个tanh激活函数，然后再进入到一个新的线性单元，这个新单元的输入tensor大小为13，输出tensor大小为1。这里需要注意的一点是，后一个模块的输入大小必须与前一个模块的输出大小一致。

seq_model = nn.Sequential(
            nn.Linear(1, 13), 
            nn.Tanh(),
            nn.Linear(13, 1)) 
seq_model

对于Sequential也可以接收OrderedDict数据结构，从而让我们为每一个模块定义一个名字。

from collections import OrderedDict

seq_model = nn.Sequential(OrderedDict([
    ('hidden_linear', nn.Linear(1, 8)), #此时我们传入的格式是1*8
    ('hidden_activation', nn.Tanh()),
    ('output_linear', nn.Linear(8, 1))
]))

seq_model

outs:
Sequential(
  (hidden_linear): Linear(in_features=1, out_features=8, bias=True)
  (hidden_activation): Tanh()
  (output_linear): Linear(in_features=8, out_features=1, bias=True)
)

既然我们能够加入激活函数和输出层，我们就可以用我们搭建的这个超级mini神经网络来训练了。

optimizer = optim.SGD(seq_model.parameters(), lr=1e-3) 
training_loop(
    n_epochs = 5000, 
    optimizer = optimizer,
    model = seq_model,
    loss_fn = nn.MSELoss(), #这里直接调用了nn模块下面的损失函数，nn模块提供了很多常见的损失函数，不再需要手动编写
    t_u_train = t_un_train,
    t_u_val = t_un_val, 
    t_c_train = t_c_train,
    t_c_val = t_c_val)
    
print('output', seq_model(t_un_val))
print('answer', t_c_val)
print('hidden', seq_model.hidden_linear.weight.grad) #我们可以把我们前面定义的命名作为一个模块来访问

outs:
Epoch 1, Training loss 206.6782, Validation loss 66.7875
Epoch 1000, Training loss 4.4289, Validation loss 2.6821
Epoch 2000, Training loss 3.9474, Validation loss 6.9495
Epoch 3000, Training loss 2.5048, Validation loss 5.1201
Epoch 4000, Training loss 2.0997, Validation loss 4.5748
Epoch 5000, Training loss 1.9665, Validation loss 4.5594
output tensor([[-1.5225],
        [12.1985]], grad_fn=<AddmmBackward0>)
answer tensor([[-4.],
        [11.]])
hidden tensor([[ 5.4156e+00],
        [ 2.9012e-01],
        [ 2.4442e-01],
        [-6.7246e+00],
        [-6.8313e+00],
        [-1.9907e-03],
        [-6.1124e+00],
        [ 1.5848e-01]])

我们这就完成了用神经网络来训练，so easy ! 从上面输出的结果，我们可以看到，使用神经网络我们获取了更低的损失，训练了5000轮之后在训练集上的损失只有1.966，不过在测试集上看起来并没有太大的区别，这似乎有点像我们前面说的过拟合，不过还不严重，属于可以接受的范围。

最后画个图，看看神经网络模拟出来的结果有什么不同

from matplotlib import pyplot as plt

t_range = torch.arange(20., 90.).unsqueeze(1)

fig = plt.figure(dpi=600)
plt.xlabel("Fahrenheit")
plt.ylabel("Celsius")
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.plot(t_range.numpy(), seq_model(0.1 * t_range).detach().numpy(), 'c-')
plt.plot(t_u.numpy(), seq_model(0.1 * t_u).detach().numpy(), 'kx')

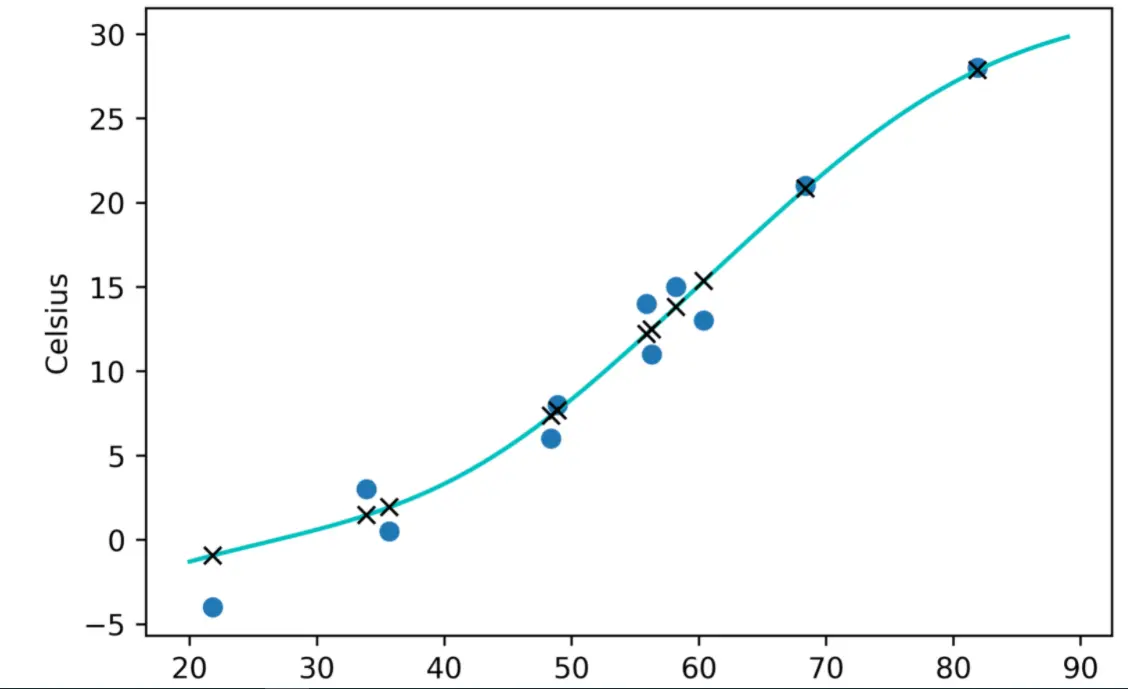
image.png

可以看到，比起之前的直线来说，我们这次获得了一条更加优雅的曲线，这个曲线对数据的拟合程度更好，当然，在这个例子中这并没有起到什么大的作用，因为我们摄氏和华氏温度的转换原本就是一条直线。

今天这节以代码为主，需要消化一下。