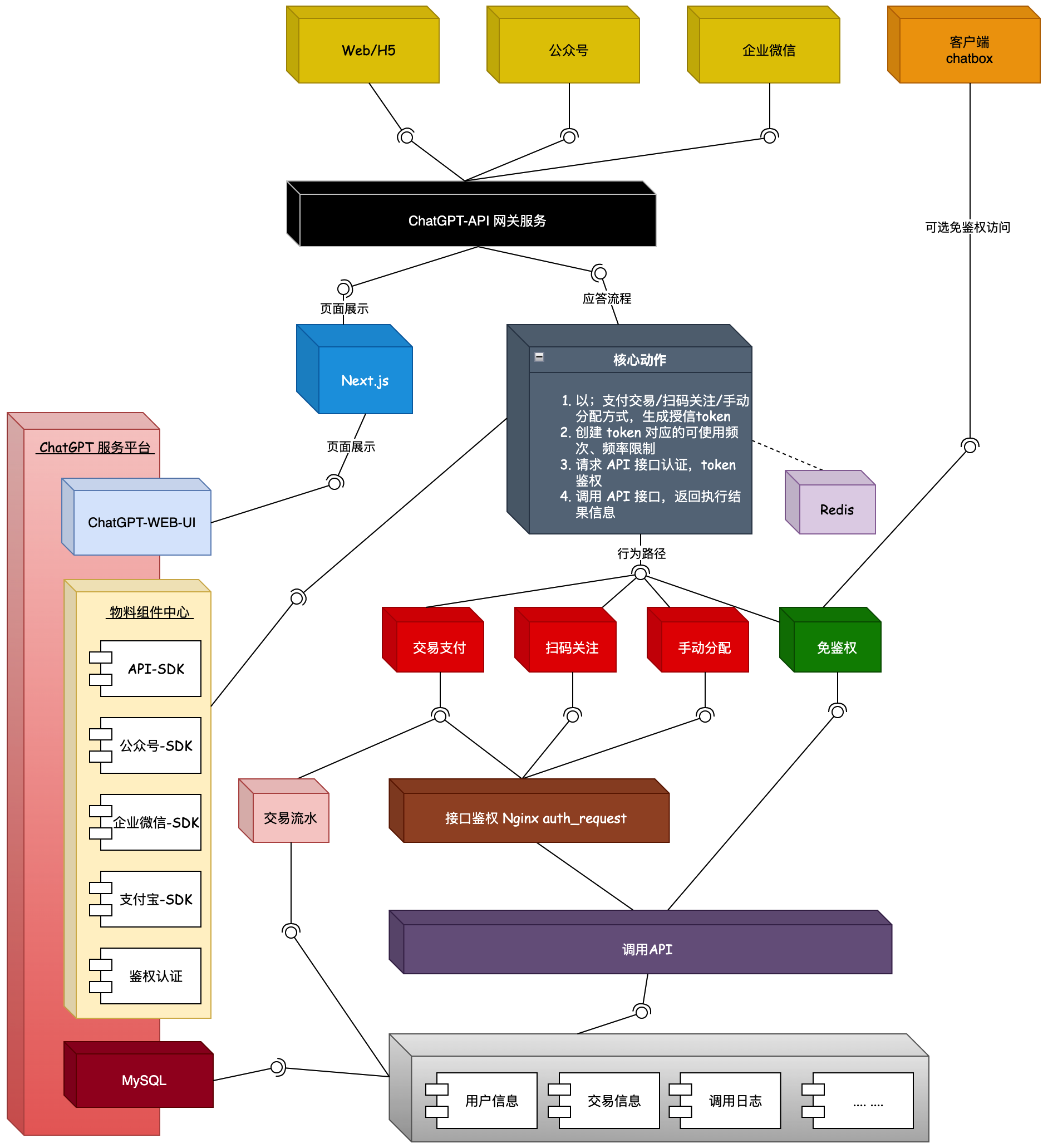
学习视觉SLAM十四讲之前的必备数学基础知识
- 1. 正交矩阵
- 2. 线性关系
- 3. 求矩阵的逆
- 4. 叉乘
- 5.反对称矩阵
- 6. 复数
1. 正交矩阵
定义: 设n阶矩阵A满足AAT=ATA=I ,则称A为正交矩阵
性质:
以下为手写,从小字丑,请多担待。。

2. 线性关系
定义: 两个变量之间存在一次方函数关系,就称它们之间存在线性关系。正比例关系是线性关系中的特例,反比例关系不是线性关系
向量的线性关系:

注意: 这里主要说明以下自己理解的线性关系分为函数线性关系和向量的线性关系,因为在SLAM中,我们使用的是向量的线性关系,因此这里主要理解向量的线性相关和无关即可。在此自己通俗的将向量的线性相关理解为
b
⃗
=
k
a
⃗
\vec{b}=k\vec{a}
b=ka,也就是函数中的正比例关系。
3. 求矩阵的逆
定义: 对于矩阵
A
∈
F
m
×
n
A\in F^{m×n}
A∈Fm×n ,如果存在
B
∈
F
m
×
n
B\in F^{m×n}
B∈Fm×n ,使得
A
B
=
I
m
∈
F
m
AB= I_m\in F^m
AB=Im∈Fm,且
B
A
=
I
m
∈
F
n
BA= I_m\in F^n
BA=Im∈Fn,则称
A
A
A可逆,称
B
B
B为
A
A
A的逆矩阵,又记作
A
−
1
A^{-1}
A−1.
逆矩阵具有唯一性!!!
这里介绍两种最简单的方法:
方法一: 待定系数法

方法二: 初等行变换
已知矩阵
A
A
A和对应维度的单位矩阵
I
I
I,先写出增广矩阵
A
∣
I
A|I
A∣I,然后对
A
A
A进行高斯消元,在对
A
A
A消元的同时,单位矩阵I也在变,直到把
A
A
A消成单位矩阵,
A
A
A旁边的单位矩阵也会随之变成
A
A
A的逆矩阵。
有两个博主对这一部分介绍的十分详细,可以参考:
https://blog.csdn.net/daduzimama/article/details/120509856
https://zhuanlan.zhihu.com/p/422839754
4. 叉乘
叉乘(Cross Product) 又称向量积(Vector Product)
在空间中有两个向量:
a
⃗
=
(
x
1
,
y
1
,
z
1
)
\vec{a}=(x_1,y_1,z_1)
a=(x1,y1,z1) ,
b
⃗
=
(
x
2
,
y
2
,
z
2
)
\vec{b}=(x_2,y_2,z_2)
b=(x2,y2,z2),
a
⃗
\vec{a}
a与
b
⃗
\vec{b}
b之间的夹角为
θ
\theta
θ。
从代数角度计算:
a
⃗
×
b
⃗
=
(
y
1
z
2
−
z
1
y
2
,
z
1
x
2
−
x
1
z
2
,
x
1
y
2
−
y
1
x
2
)
\vec{a}×\vec{b}=(y_1z_2-z_1y_2,z_1x_2-x_1z_2,x_1y_2-y_1x_2)
a×b=(y1z2−z1y2,z1x2−x1z2,x1y2−y1x2)
从几何角度计算:(
n
⃗
\vec{n}
n为
a
⃗
\vec{a}
a与
b
⃗
\vec{b}
b所构成平面的单位向量)
a
⃗
×
b
⃗
=
∣
a
⃗
∣
∣
b
⃗
∣
s
i
n
θ
n
⃗
\vec{a}×\vec{b}=|\vec{a}||\vec{b}|sin\theta\vec{n}
a×b=∣a∣∣b∣sinθn
其运算结果是一个向量,并且与这两个向量都垂直,是这两个向量所在平面的法线向量。使用右手定则确定其方向。

几何意义:
如果以向量
a
⃗
\vec{a}
a和
b
⃗
\vec{b}
b为边构成一个平行四边形,那么这两个向量外积的模长与这个平行四边形的面积相等。

参考文章:https://zhuanlan.zhihu.com/p/148780358
5.反对称矩阵
定义: 设
A
A
A为
n
n
n维方阵,若有
A
T
=
−
A
A^T=-A
AT=−A,则称矩阵
A
A
A为反对称矩阵。
对于反对称矩阵,它的主对角线上的元素全为零,而位于主对角线两侧对称的元素反号。
反对称矩阵具有很多良好的性质,如若
A
A
A为反对称矩阵,则
A
T
,
λ
A
A^T,λA
AT,λA均为反对称矩阵;
若
A
,
B
A,B
A,B均为反对称矩阵,则
A
±
B
A±B
A±B也为反对称矩阵;
设
A
A
A为反对称矩阵,
B
B
B为对称矩阵,则
A
B
−
B
A
AB-BA
AB−BA为对称矩阵;
奇数阶反对称矩阵的行列式必为0。反对称矩阵的特征值是0或纯虚数,并且对应于纯虚数的特征向量的实部和虚部形成的实向量等长且互相正交。
性质:

6. 复数
复数由实部和虚部组成,复数相加时实部和实部相加,虚部和虚部相加,复数相乘时则利用
i
2
=
1
i^2 =1
i2=1。
有关复数的介绍,发现了一篇质量较高的文章:https://zhuanlan.zhihu.com/p/94300315
这里我们主要说一下复数中存在的运算,
q
1
=
a
+
b
i
,
q
2
=
c
+
d
i
q_1=a+bi,q_2=c+di
q1=a+bi,q2=c+di
复数的加法运算
q
1
+
q
2
=
(
a
+
b
i
)
+
(
c
+
d
i
)
=
(
a
+
c
)
+
(
b
+
d
)
i
q_1+q_2=(a+bi)+(c+di)=(a+c)+(b+d)i
q1+q2=(a+bi)+(c+di)=(a+c)+(b+d)i
复数的减法运算
q
1
+
q
2
=
(
a
+
b
i
)
−
(
c
+
d
i
)
=
(
a
−
c
)
+
(
b
−
d
)
i
q_1+q_2=(a+bi)-(c+di)=(a-c)+(b-d)i
q1+q2=(a+bi)−(c+di)=(a−c)+(b−d)i
复数的乘法运算
q
1
q
2
(
a
+
b
i
)
(
c
+
d
i
)
=
(
a
c
−
b
d
)
+
(
b
c
+
a
d
)
i
q_1q_2(a+bi)(c+di)=(ac-bd)+(bc+ad)i
q1q2(a+bi)(c+di)=(ac−bd)+(bc+ad)i
复数的模长
∣
q
1
∣
=
a
2
+
b
2
,
∣
q
2
∣
=
c
2
+
d
2
,
∣
q
1
q
2
∣
=
∣
q
1
∣
∣
q
2
∣
|q_1|=\sqrt{a^2+b^2},|q_2|=\sqrt{c^2+d^2},|q_1q_2|=|q_1||q_2|
∣q1∣=a2+b2,∣q2∣=c2+d2,∣q1q2∣=∣q1∣∣q2∣
复数的共轭
共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。当虚部不为零时,共轭复数就是实部相等,虚部相反,如果虚部为零,其共轭复数就是自身(当虚部不等于0时也叫共轭虚数)。复数z的共轭复数记作
z
z
z(上加一横),有时也可表示为
Z
∗
Z*
Z∗。同时, 复数
z
z
z(上加一横)称为复数z的复共轭(complex conjugate)。

复数的逆:
q
−
1
=
q
∗
/
∣
q
∣
2
q^{-1}=q^*/|q|^2
q−1=q∗/∣q∣2
按此定义,
q
q
−
1
=
q
−
1
q
=
1
qq^{-1} = q^{-1}q=1
qq−1=q−1q=1
目前知道这些知识后,在第三中是可用的。