回溯算法本质

回溯算法的本质是穷举，即对所有可能的情况进行一一穷举，如果求解过程中发现某个情况不符合求解要求，直接进行剪枝即可

回溯算法模板

我们可以将回溯算法理解为以下两种模板

1.递归回溯

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

2.多叉树的遍历

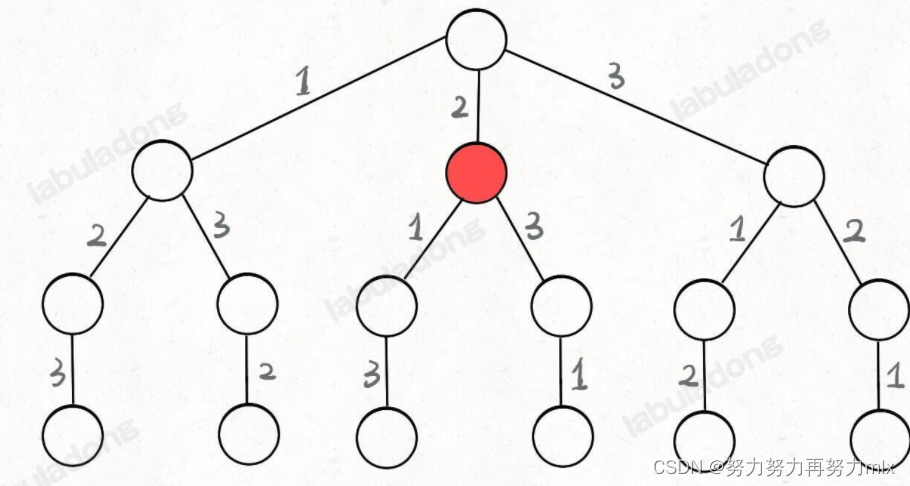
void traverse(TreeNode root) {
    for (TreeNode child : root.childern) {
        // 前序位置需要的操作
        traverse(child);
        // 后序位置需要的操作
    }
}

题目实例

题目描述

力扣https://leetcode.cn/problems/permutations/

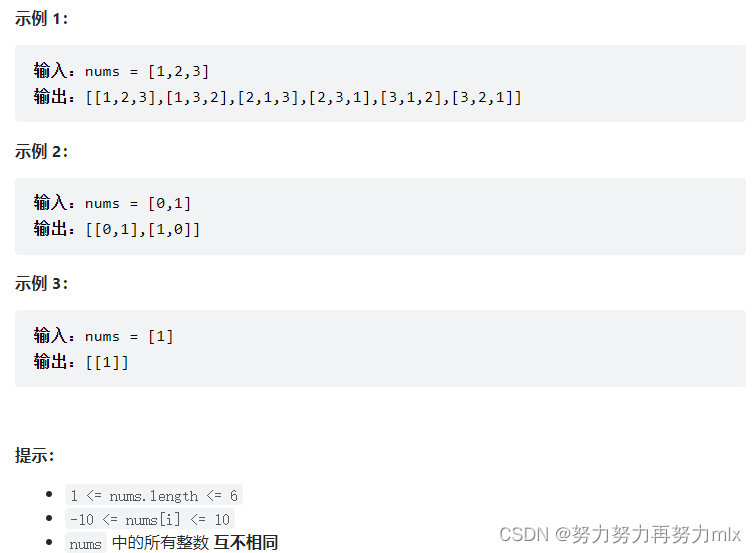
给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

解题思路

对于回溯算法的题目，我们直接修改小部分的算法策略后直接套用回溯模板即可：针对这道题目，我们的实现思路如下：对于每一层数字的排列，我们一一穷举其可能的情况，之后将可能的情况进行保存，不可能的情况直接丢弃，在可能情况的基础上进行下一层的递归遍历，在递归最后一层数字后将代码进行回溯~

代码实现

class Solution {
    //定义结果集
    private LinkedList<List<Integer>> res=new LinkedList<>();
    public List<List<Integer>> permute(int[] nums) {
        //调用递归函数
        //创建列表
        LinkedList<Integer>list=new LinkedList<>();
        reverse(list,nums);
        return res;
    }
    //创建递归函数
    public void reverse(LinkedList<Integer>list,int[]nums){
        //判断递归的终止条件
        if(list.size()==nums.length){
            //导出
            res.addLast(new LinkedList(list));
        }
        //进入递归
        for(int i=0;i<nums.length;++i){
            if(list.contains(nums[i])){
                continue;
            }
            //加入列表
            list.addLast(nums[i]);
            //递归
            reverse(list,nums);
            list.removeLast();
        }
    }
}

题目描述

N皇后问题

解题思路

N皇后问题也是直接套用模板即可：在每一层皇后的选择中遍历所有情况，将不符合条件的情况进行摒弃，继续向下一层进行递归遍历，直到满足所有情况后进行回溯即可

代码实现

public class NEmpress {
    private static final  int N=8;
    public static int process(int[]data,int i,int n){
        //定义计数器
        int res=0;
        if(i==n){
            return 1;
        }
        //进行递归遍历
        for(int j=0;j<n;++j){
            //判断当前列是否有效
            if(isValid(data,i,j)){
                data[i]=j;
            }
            //递归
          res+=process(data, i+1, n);
            //回溯
            data[i]=0;
        }
        return res;
    }

    private static boolean isValid(int[] data, int i, int j) {
        for(int k=0;k<i;++k){
            if(data[k]==j||Math.abs(i-k)==Math.abs(j-data[k])){
                return false;
            }
        }
        return true;
    }
}