欢迎
- 前言
- 一、动态规划五部曲
- 二、下降路径最小和
- 思路:动态规划解法
- 具体代码如下
- 三、礼物的最大价值
- 思路:动态规划
- 具体代码如下:
- 总结
前言
本文主要讲述动态规划思路的下降路径最小和以及礼物的最大价值两道题。
一、动态规划五部曲
- 1.确定状态表示(确定dp数组的含义)
- 2.确定状态转移方程(确定dp的递推公式)
- 3.确定如何初始化(初始化要保证填表正确)
- 4.确定遍历顺序
- 5.返回值
二、下降路径最小和
点我直达
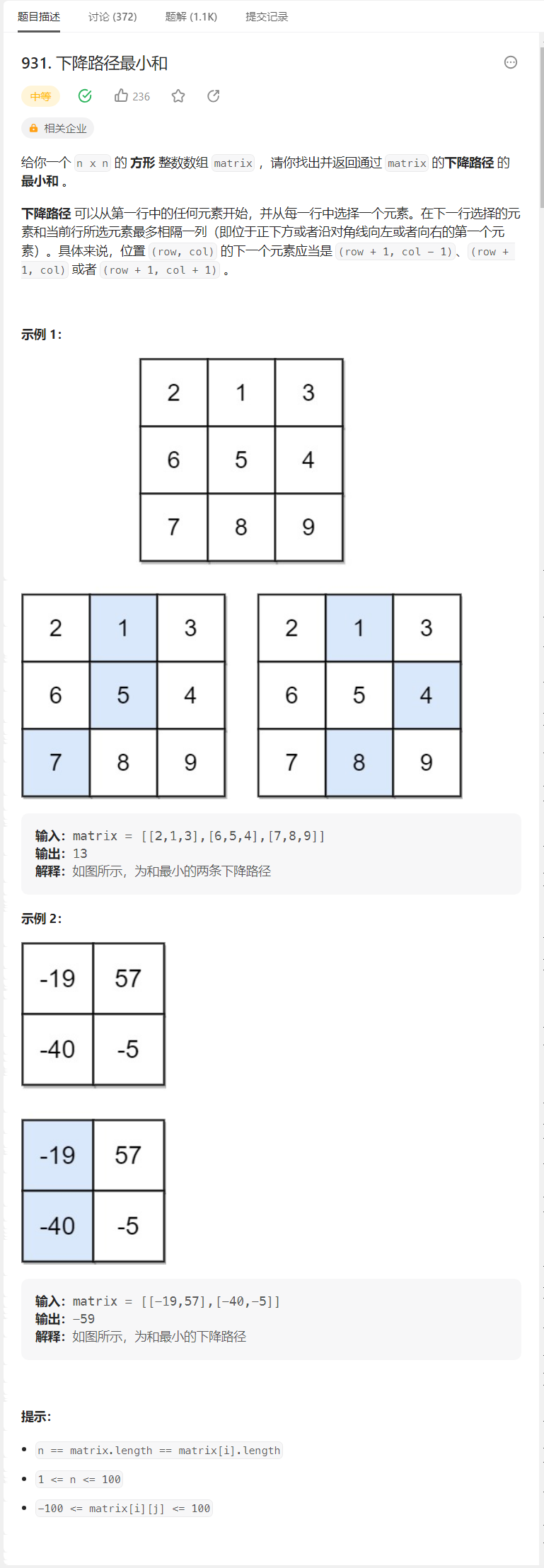
思路:动态规划解法
-
1.确定状态表示,即确定dp数组的含义。
-
- 写动态规划的题目,确定状态表示是最重要的一步,如何确定呢?往往需要经验+题目描述,就需要大量的动态规划问题基础。
在本题中,我们需要使用二维dp数组来表示下降路径,所以dp数组的含义是:
第[i,j]位置的最小下降路径为dp[i][j]。
- 写动态规划的题目,确定状态表示是最重要的一步,如何确定呢?往往需要经验+题目描述,就需要大量的动态规划问题基础。
-
2.确定状态转移方程(确定递推公式)
-
- 根据题目描述,第[i,j]位置是由第[i-1,j-1],[i-1,j],[i-1,j+1]三个位置的任意一个往下走得来,如下图。
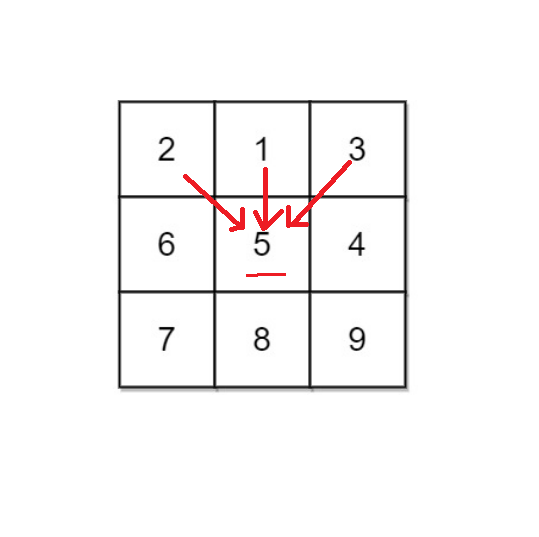
所以我们可以确定,dp[i][j]一定与dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1]有关。
我们再回顾dp数组的含义:dp[i][j] :第[i,j]位置的最小下降路径为dp[i][j]
所以下降到第[i,j]的位置时,一定是由[i-1,j-1],[i-1,j],[i-1,j+1]三个位置的对于的最小dp值+当前位置的路径。
即:dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+ob[i][j],其中ob为题目给出的二维数组。
- 根据题目描述,第[i,j]位置是由第[i-1,j-1],[i-1,j],[i-1,j+1]三个位置的任意一个往下走得来,如下图。
-
3.如何初始化
-
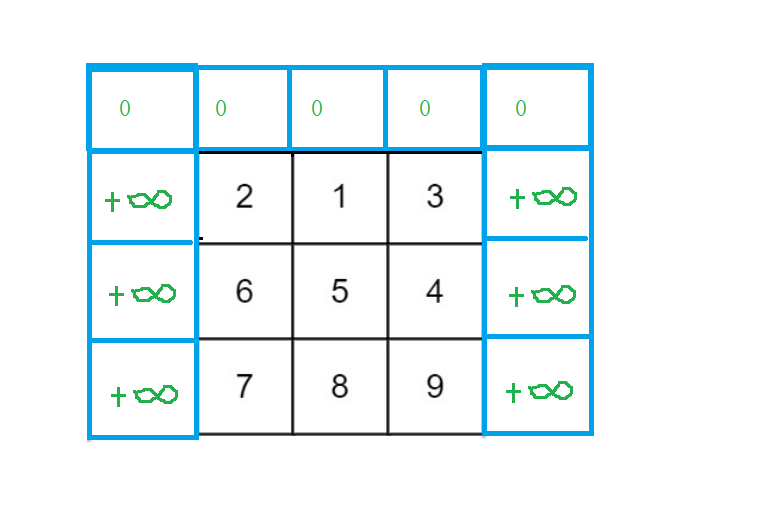
- 细心的小伙伴会发现,第一行的数据,dp[0][j]是如何推导的呢?如果仅仅开辟题目给出的ob数组大小的dp数组空间,是无法初始化完全的。所以我们给出了一个多开辟虚拟空间的解决方案。如下图:
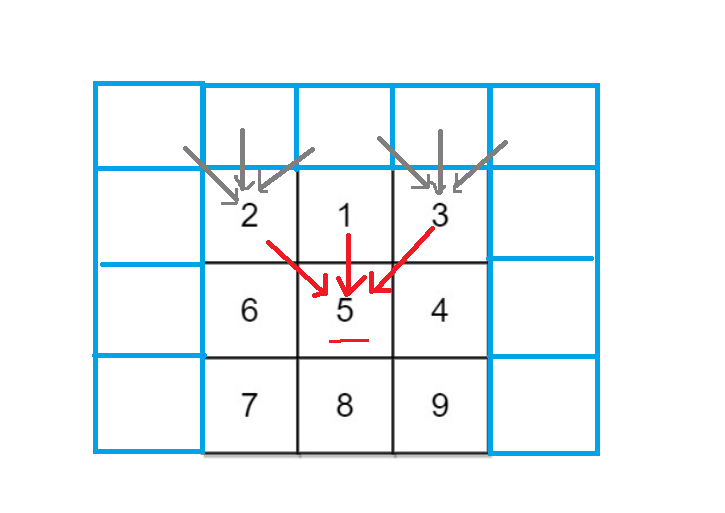
我们多开一行两列的空间,这样就满足了任意位置都能直接被便利到。
但开辟虚拟空间需要注意两个问题:
1.虚拟位置的初始化必须保证原dp数组正确。
2.注意下标的映射关系。
- 细心的小伙伴会发现,第一行的数据,dp[0][j]是如何推导的呢?如果仅仅开辟题目给出的ob数组大小的dp数组空间,是无法初始化完全的。所以我们给出了一个多开辟虚拟空间的解决方案。如下图:
-
-
- (1)我们应该初始化第一行虚拟空间为0,这样保证了原dp数组的初始化不受影响。
再初始化第一列和第n+1列为正无穷大。
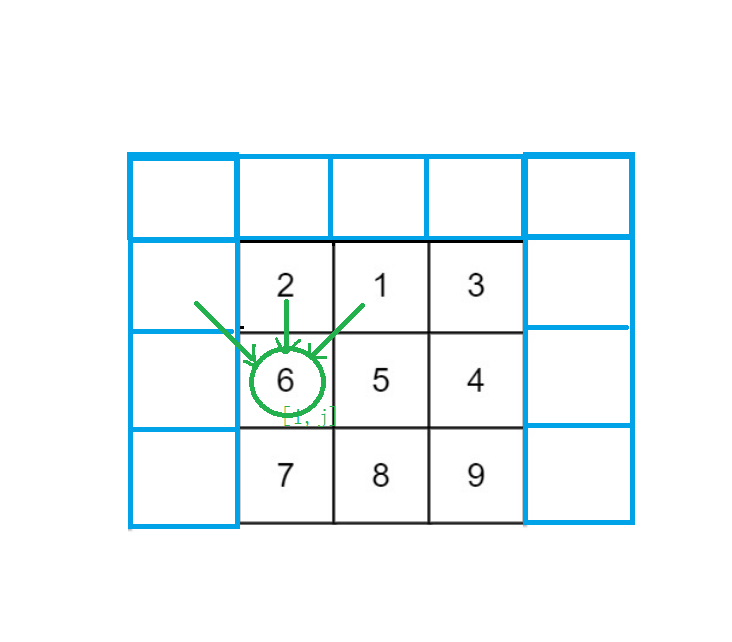
- (1)我们应该初始化第一行虚拟空间为0,这样保证了原dp数组的初始化不受影响。
-
以图中数字为例,第[i-1,j-1]位置,也就是左上角位置是虚拟开辟出来的,所以必须要保证这个位置初始化的时候不能影响原数组的初始化。所以我们应该在这个虚拟位置初始化成正无穷大。就保证永远取不到这个地方。
-
-
- (2)注意下标的映射关系,以上图为例,
dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+ob[i-1][j-1],注意这里是+ob[i-1][j-1]而不是+ob[i][j],因为虚拟数组多开了一行两列,所以整体的元素都往右下角挪了一个位置,所以找原位置是必须回到左上角。
- (2)注意下标的映射关系,以上图为例,
-
-
4.确定遍历顺序
-
- 根据上述描述,和递推公式,可以知道我们只能从上往下进行遍历。
-
5.返回值
-
- 当遍历到最后一行时,我们应该知道,题目要求返回下降路径最小和,在最后一行中,每一个元素都是从上往下的下降路径最小的数,所以我们应该比较这最后一行元素中的最小值,返回即可。
具体代码如下
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& ob)
{
//1.确定dp[i][j]的含义:下降到i,j位置的最小路径为dp[i][j]
//2.递推公式:
//dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+ob[i][j]
//3.初始化dp数组,多开一行,两列的虚拟空间,全部初始化为0
//对虚拟空间的要求:1.里面的值要保证后面填表正确
//2.要注意下标的映射
//4.遍历顺序,只能从上到下遍历。
//5.返回值,返回最后一行的最小值
int n = ob.size();
vector<vector<int>> dp(n+1,vector<int>(n+2,0));
for(int i = 1;i<=n;i++)
{
dp[i][0] = INT_MAX;
dp[i][n+1] = INT_MAX;
}
// vector<vector<int>> dp(n+1,vector<int>(n+2,INT_MAX));
//第一行全部初始化成0,但是第一列和最后一列的第二行开始,就初始化成正无穷大
// for(int i = 0;i< n+2;i++)
// {
// dp[0][i] = 0;
// }
for(int i = 1;i<= n ;i++)
{
for(int j = 1;j<= n;j++)
{
dp[i][j] = min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1]))+ob[i-1][j-1];
}
}
int ret = INT_MAX;
//遍历dp表的最后一行,选出最小值
for(int i = 1;i<=n;i++)
{
ret = min(ret,dp[n][i]);
}
}
};
时间复杂度O(n^2), 空间复杂度O(n^2)
三、礼物的最大价值
点我直达~

思路:动态规划
- 1.状态表示(确定dp数组的含义)
根据经验和题目描述可知,
dp[i][j]表示:到达第[i,j]位置拿到的礼物最大价值为dp[i][j]. - 2.状态转移方程(确定递推公式)
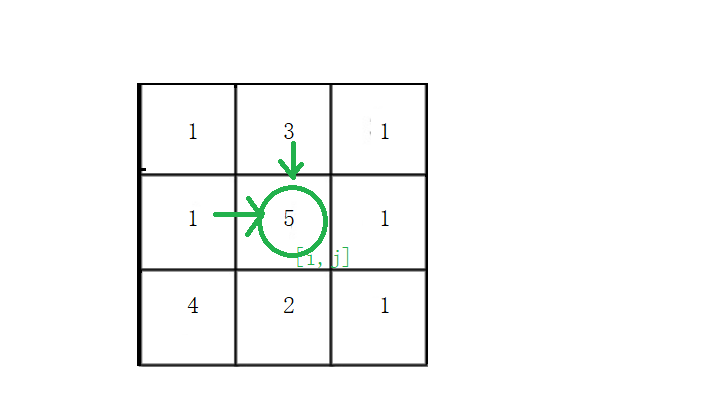
由图可知,走到第[i,j]位置一定是由它的上方往下走一步或者它的左侧往右走一步得来。所以dp[i][j]一定跟dp[i-1][j]和dp[i][j-1]有关。
再回顾一下dp数组的含义:到达第[i,j]位置拿到的礼物最大价值为dp[i][j]
那么由此我们可以确定递推公式:
dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + grid[i][j],其中grid是题目给出的数组。
可以发现本道题的思路与上一题类似。
- 3.如何进行初始化
有了上道题目的经验,我们发现,第一行的元素无法初始化,因为它没有上方的元素和左方的元素。所以我们应该多开辟一行一列的虚拟数组,如下图:
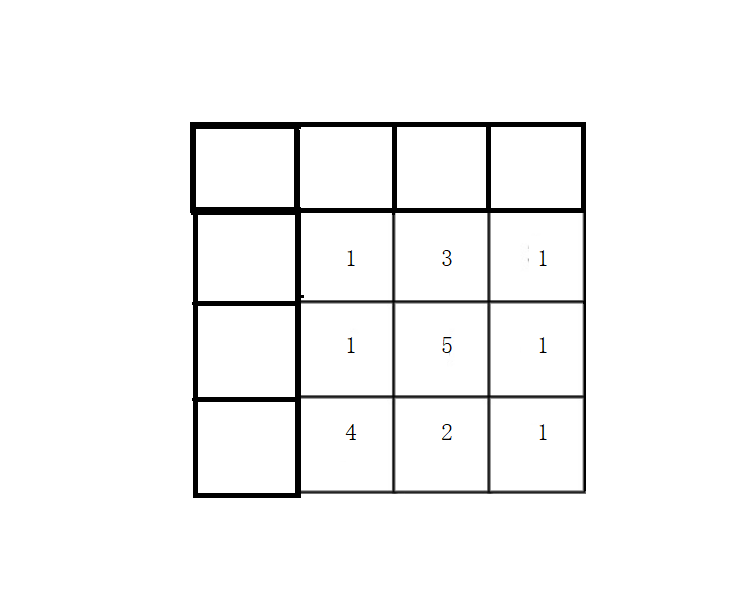
同理:需要注意两个问题,
1.虚拟位置的初始化必须保证原dp数组正确。
2.注意下标的映射关系。
所以我们应该初始化成0,这样在虚拟空间不会被选中,对原数组不产生影响。
那么下标的映射关系也是如此:
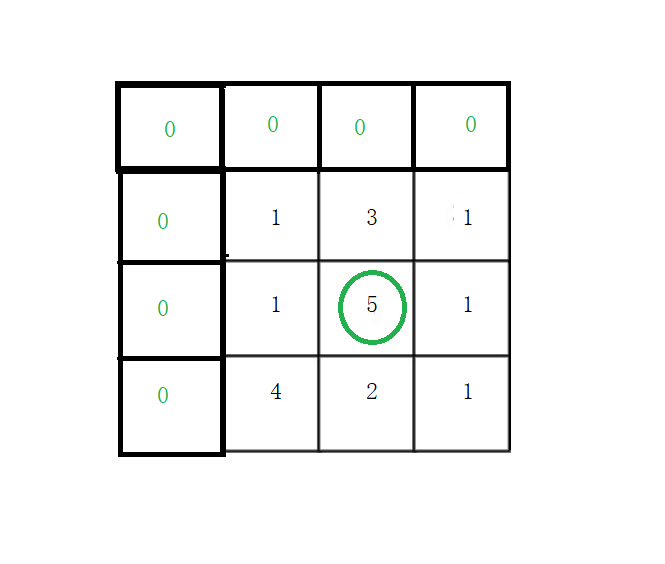
假如对想求出图中位置的dp值,应该为:
dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + grid[i-1][j-1],因为我们多开了一行一列的数组,所以这里原数组整体往右下角移动了一位,要找到原来的值,需要挪动回到左上角查找。
-
4.确定初始化顺序
由上面的分析可知,我们应该从上往下初始化,从左往右初始化。 -
5.返回值
-
返回右下角的值即可。
具体代码如下:
class Solution {
public:
int maxValue(vector<vector<int>>& grid)
{
int m = grid.size();
int n = grid[0].size();
vector<vector<int>>dp(m+1,vector<int>(n+1));
for(int i = 1;i<=m;i++)
{
for(int j = 1;j<=n;j++)
{
dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + grid[i-1][j-1];
}
}
return dp[m][n];
}
};
时间复杂度O(m*n),空间复杂度O(m*n)
总结
今天学到了一个动态规划的点:多开辟一块空间,使得初始化变得更为简单,但是也要注意两个点:
1.虚拟位置的初始化必须保证原dp数组正确。
2.注意下标的映射关系。
](https://img-blog.csdnimg.cn/f4125da150c448d79014f6d0bb6c465e.png)