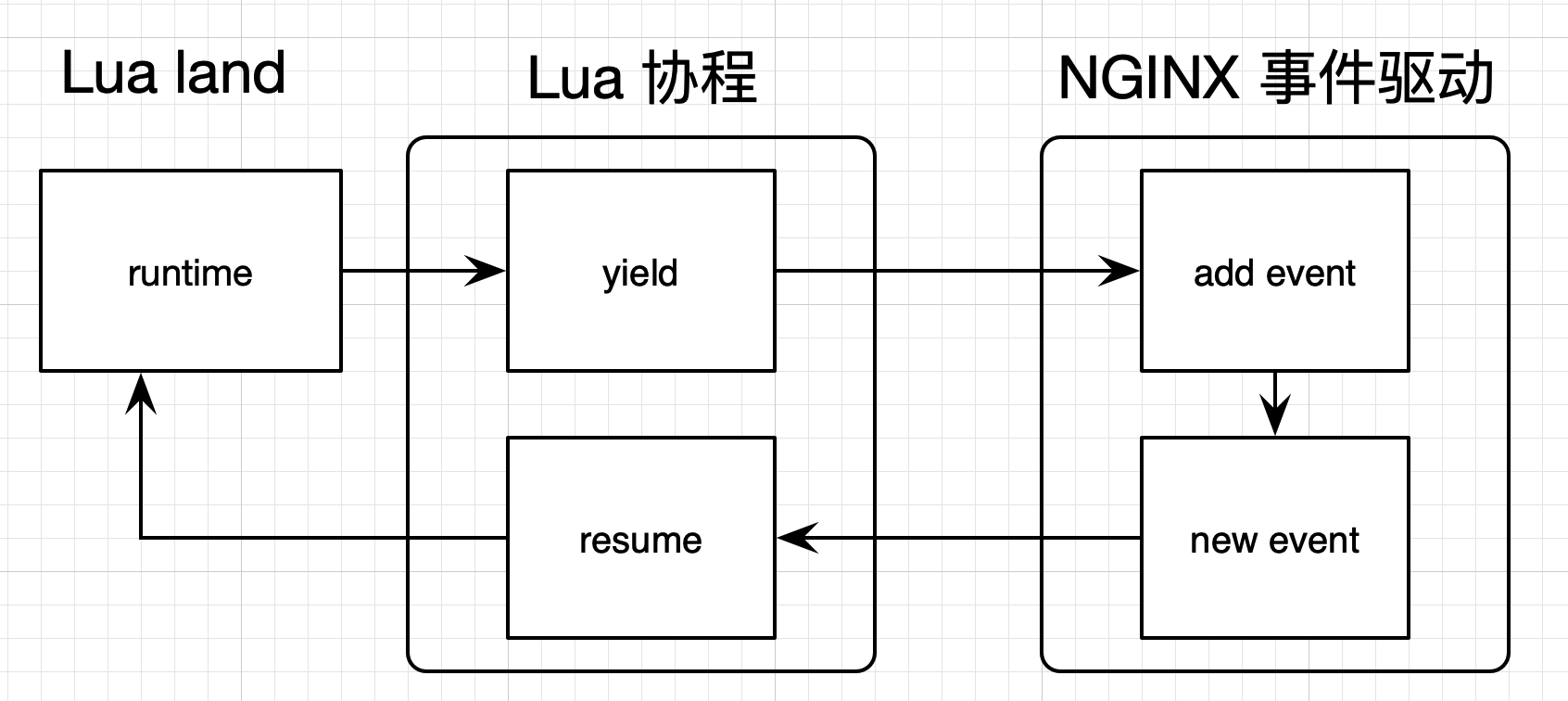
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 一、动态规划
- 二、动态规划五部曲
- 1.确定DP数组的含义
- 2.确定递推公式
- 3.确定初始值
- 4.确定遍历顺序
- 5.举例推导DP数组,打印程序中DP数组日志
- 三、例子
一、动态规划
动态规划的英文是Dynamic Programming,简称DP,如果某一个问题可以由很多重叠的子问题组成,那么这个问题可以使用动态规划解决。思想是动态规划中的每一个状态一定是由上一个状态推导出来的,这一点与贪心算法不一样,没有状态推导,贪心是局部最优,而且局部最优可以构成全局最优。
二、动态规划五部曲
此部分学习了代码随想录的动态规划。
1.确定DP数组的含义
2.确定递推公式
3.确定初始值
4.确定遍历顺序
5.举例推导DP数组,打印程序中DP数组日志
接下来举例子,按照这五部曲来解题。
三、例子
例1,力扣70题–爬楼梯
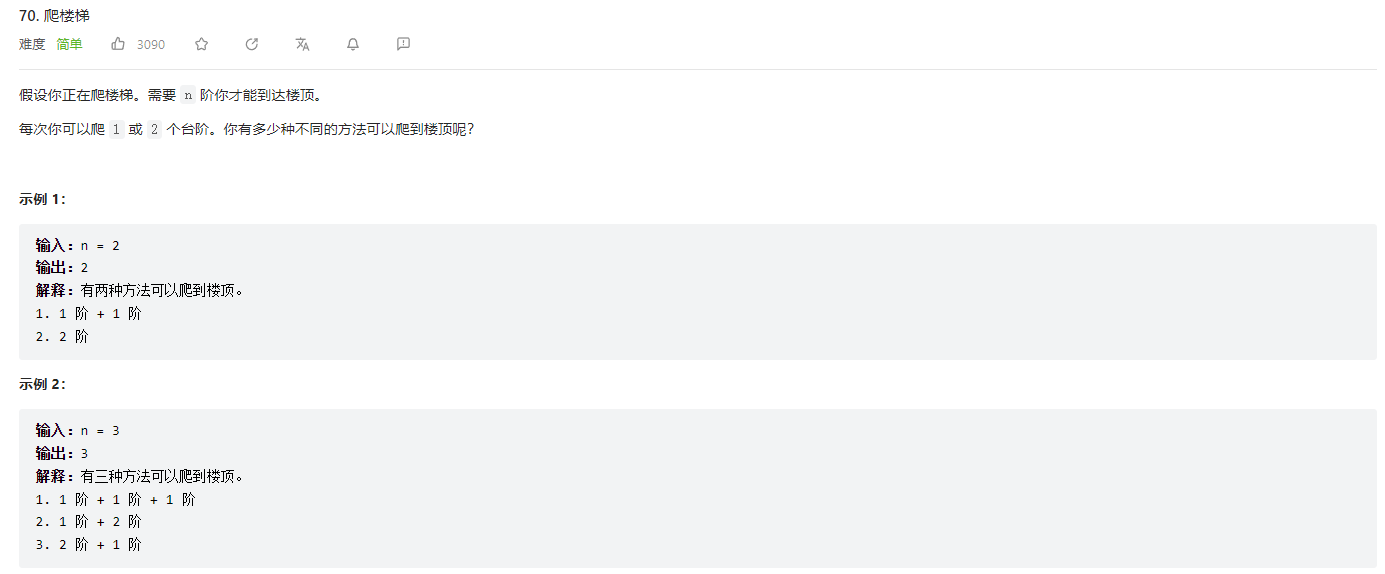
分析题目为什么可以用动态规划的方法呢?假设F(n)代表了由F(n)种方法可以到达n个台阶的楼顶,而题目说了每次爬1个或者2个台阶,所以F(n)应该可以由F(n-1) + F(n-2)得到,即是将原问题拆分成了很多子问题,而且改状态是由上一个状态得到的。满足动态规划的思想。
现在用动态规划五部曲的步骤分析一下这道题目:
(1)确定DP数组的含义,dp[i]代表了有dp[i]种方法可以到达i个台阶的楼顶。
(2)确定递推关系,dp[i] = dp[i-1] + dp[i-2],因为一次只能上1个台阶或者2个台阶。
(3)确定初始值,dp[1] = 1,dp[2] = 2
(4)确定遍历顺序,应该是从前往后遍历
(5)推导DP数组,从程序中打印DP数组日志
写出来的代码如下
class Solution:
def climbStairs(self, n: int) -> int:
dp = [1,2]
sum_ = 0
if n <=2:
return n
else:
for i in range(3,n+1):
sum_ = dp[0] + dp[1]
dp[0] = dp[1]
dp[1] = sum_
return dp[1]
这样实现的时间复杂度是O(n),空间复杂度是O(1),做了优化。
例2,力扣53
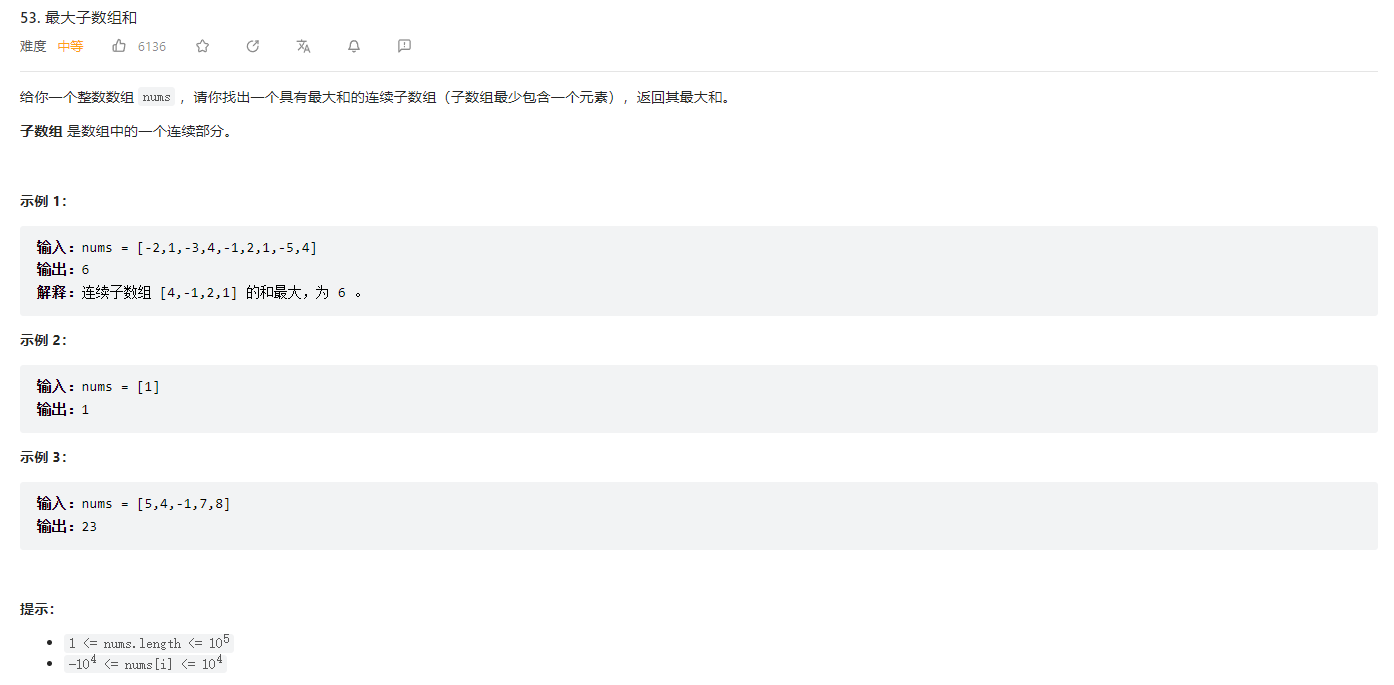
这个题为什么可以用到动态规划的思想呢?
如果把遍历方式定义为以i结尾的连续数组,遍历的结果就是如下:
[-2],[-2,1],[-2,1,-3],[-2,1,-3,4],[-2,1,-3,4,-1],[-2,1,-3,4,-1,2],[-2,1,-3,4,-1,2,1],[-2,1,-3,4,-1,2,1,-5],[-2,1,-3,4,-1,2,1,-5,4]。
进而把原问题分解为如下子问题:求每一个遍历序列的最大值,这样后一个问题就可以有前一个问题递推得到,dp[i] = max(dp[i-1] + nums[i],nums[i])。
按照动态规划五部曲来分析该问题
(1)确定DP数组的含义,dp[i]代表了遍历到第i个序列的最大和。
(2)确定递推关系,dp[i] = max(dp[i-1] + nums[i],nums[i])。
(3)确定初始值,dp[0] = nums[0]
(4)确定遍历顺序,从i=1开始遍历,从小到大遍历
(5)推导DP数组,从程序中打印DP数组日志
代码如下:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
##第一步:dp数组的含义,dp[i]表示以nums[i]结尾的最大和的连续子数组
##第二步:状态转移方程,dp[i] = max(dp[i-1] + nums[i],nums[i])
##第三步:初始化,dp[0] = nums[0]
##第四步:遍历顺序,从左往右
dp = []
dp.append(nums[0])
for i in range(1,len(nums)):
dp.append(max(dp[i-1] + nums[i],nums[i]))
return max(dp)