注：目前没有精力去美化排版，所有博客仅作为自己学习记录所用

《线性代数的本质》课程链接（bilibili）

目录：

P1-P4的内容：

1.线性代数的加法：为什么这样子来定义呢（如图）

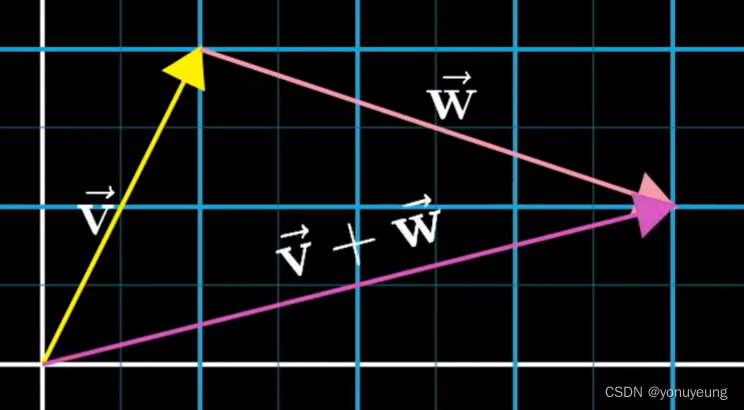
从结果上看，走上面这条路的结果与下面这条路的结果是一样的

2.每当我们用数字描述向量时，它都在依赖于我们使用的基，所以两个数乘向量的组合又被称为这个两个向量的线性组合。那“线性”又是什么东西呢？当我们固定其中一个标量，让另外一个标量自由变化，所产生的向量的终点会描出一条直线，这就是线性。

 

3.当你考虑一个向量时，也许会把它看成一条有方向的线段，当考虑多个向量时，应该把他们看成点

4.当你有多个向量，移除其中一个而不减小张成的空间时，我们就称他们为线性相关。换一种表达方式就是，其中一个向量，可以表示为其他向量的线性组合，即这个向量已经落在其他向量张成的空间中。
如果向量给张成的空间增加了新的维度，它们就被称为“线性无关”。

5.线性代数里面最精彩也是最重要的一部分——线性变换。直观的说，如果一个变换具有以下这两个性质，我们就称它们为线性变换：①原点必须保持固定   ②直线在变换后依旧是直线，不会发生弯曲。总的来说，线性变换就是保持网格线平行且等距分布

6.理解向量的乘法运算（为什么计算向量的乘法的时候，是横的一行乘竖的一行？）：

一个二维线性变换仅由四个数字（变换后 i 帽的坐标和变换后 j 帽的坐标 ）完全决定

把它们写成一个2*2的矩阵

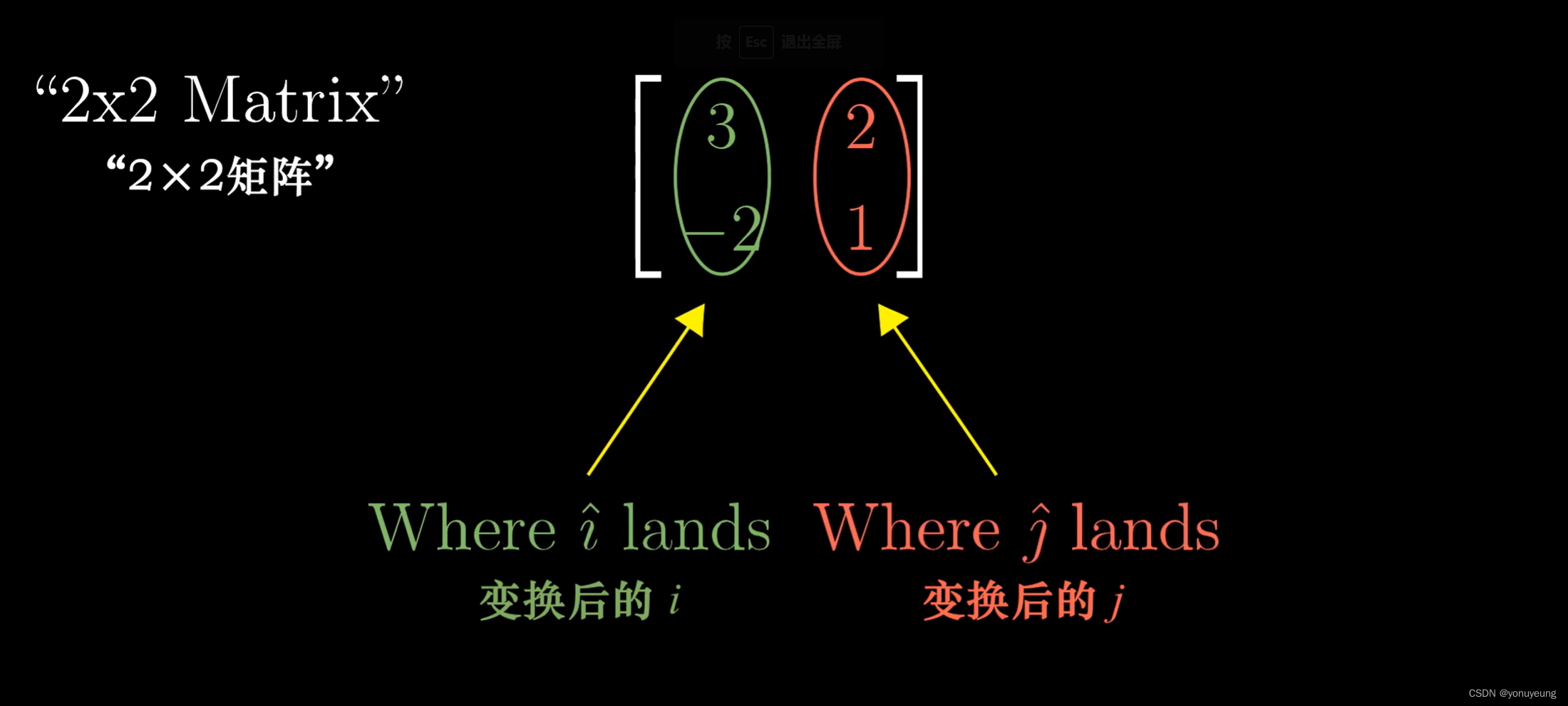
现在再给定一个向量[5,7]T，想了解这种变换对该向量的影响，只需要拿出对应的坐标分别与矩阵的特定列相乘，然后将结果相加

 

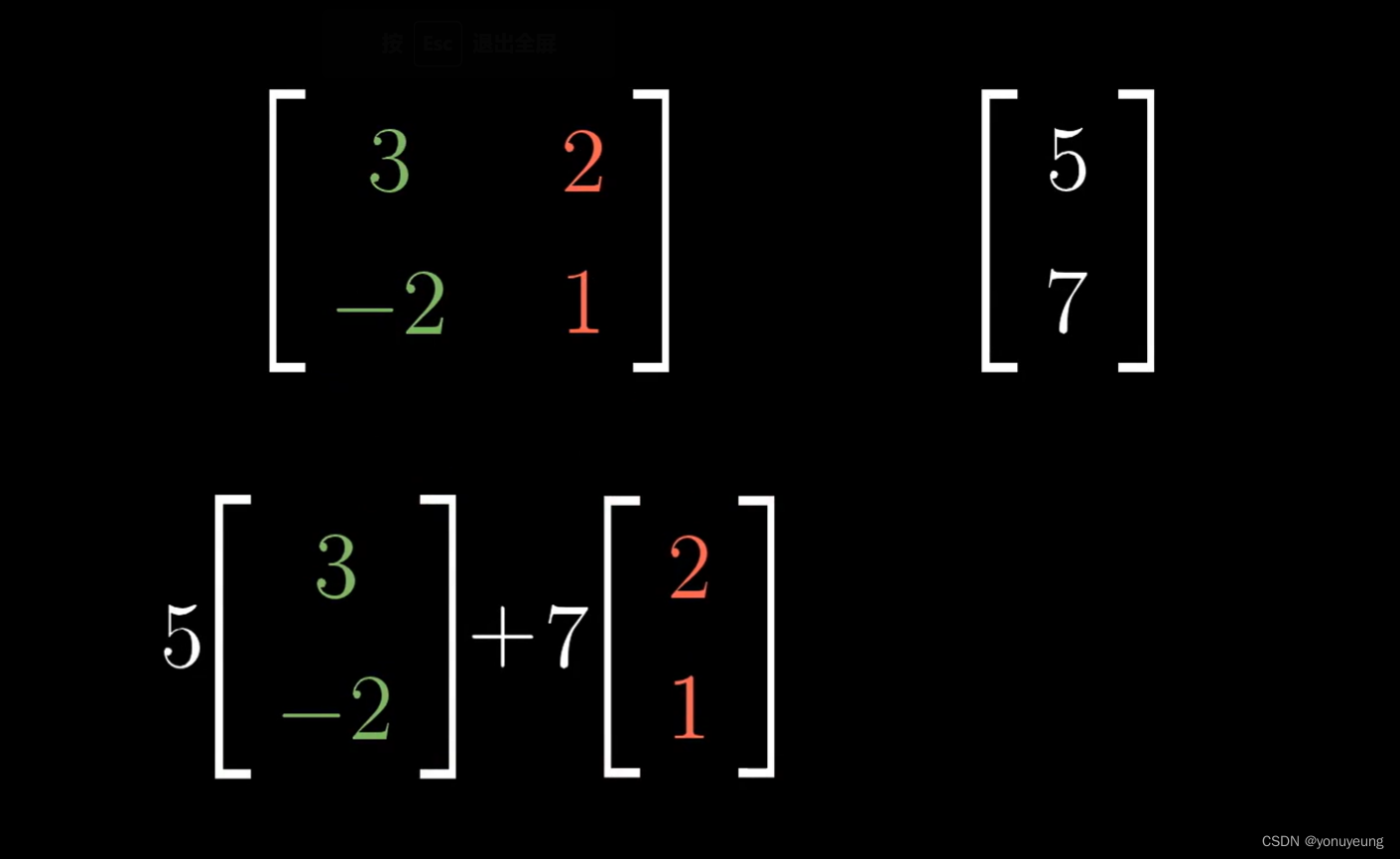
 总结成一般形式，就是：

 这就是矩阵向量乘法

类似于这样，我们可以把矩阵的列看作变换后的基向量，把矩阵向量乘法看作它们的线性组合

练习：用矩阵描述一些线性变换：将整个空间逆时针旋转90度

 

 总之：线性变换是一种操纵空间的手段

深刻理解线性代数：每当你看到一个矩阵时，你都可以把它解读为对空间的一种特定变换

当你将矩阵看作空间的变换之后，此后几乎所有有关线性代数的主题都会更加容易

P5-P 的内容

1.矩阵乘法是怎么定义的呢？

比如我们想描述一个操作：先将空间逆时针旋转90度，然后再对空间进行剪切。

单独的对这两个操作，我们有两个矩阵。对变换的最终结果，我们有一个矩阵，我们希望，前面这两个矩阵之间的乘法能够得到后面这个矩阵，于是就定义出了矩阵乘法。

2.通过对矩阵乘法的深刻理解，从而明白为什么M1M2≠M2M1，为什么A(BC)=(AB)C