一、从线性回归到逻辑回归
对于分类问题,我们该如何解决
可以通过线性回归+阈值解决吗?

就上面的这张图而言,横轴蓝色的那条线是可以将正负样本区分开的。那我们再看一个例子

就上面的图而言,横轴蓝色的那条线无法将正负例正确划分。因此,在有噪声点的情况下,阈值偏移大,健壮性不够。换句话说,直接用线性回归+阈值的方法是不能解决分类问题的。
二、逻辑回归决策边界
在逻辑回归(Logistic Regression)里,通常我们并不拟合样本分布,而是确定决策边界,如下图所示各式各样的决策边界。

在逻辑回归中,我们考虑使用sigmoid函数将线性回归的结果压缩为0-1之间的数,将该数看作预测为正例的概率。sigmoid的函数形式以及图形式如下所示
�(�)=11+�−�
�(�)′=�(�)∗(1−�(�))

在逻辑回归中,如果我们的线性回归是用线性函数来表示的,那么逻辑回归最终得到线性决策边界;如果我们的线性回归是用非线性函数来表示的,那么逻辑回归最终得到非线性决策边界。如下面的图所示。


三、逻辑回归损失函数
3.1 损失函数
我们首先考虑线性回归中使用的均方差损失函数来做为逻辑回归的损失函数,但是如果逻辑回归的损失函数用均方差损失函数,它对应的损失函数会是一个非凸函数,那么就难以找到最优解。如下图所示。

我们希望损失函数是凸函数,这样可以方便我们求解最优解,如下图所示。

从而引入了对数损失/二元交叉熵损失作为逻辑回归的损失函数

对这个公式进行理解,首先ℎ�(�)表示将样本预测为正例的概率,当y=1(正例)时,我们希望 ℎ�(�) 越大越好,那就是 ���(ℎ�(�)) 越大越好,那么就是 −���(ℎ�(�)) 越小越好,那也就是最小化损失函数的问题;当y=0(负例)时,我们希望ℎ�(�)越小越好,那就是1-ℎ�(�)越大越好,那就是 ���(1−ℎ�(�)) 越大越好,那就是
-���(1−ℎ�(�))越小越好,那也就是最小化损失函数的问题。
将上面2个式子合并,以及考虑所有样本,得到逻辑回归的最终损失函数形式:

3.2 损失函数的正则化
仍然可能存在过拟合问题,决策边界可能"抖动很厉害"。所以我们对损失函数添加正则项,得到如下的损失函数。

3.3 损失函数的最小化
逻辑回归的损失函数是凸函数,依旧可以用梯度下降。

四、从二分类到多分类
LR是一个传统的二分类模型,它也可以用于多分类任务,其基本思想是:将多分类任务拆分程若干个二分类任务,然后对每个二分类任务训练一个模型,最后将多个模型的结果进行集成以会获得最终的分类结果。一般来说,可以采用的拆分策略有:
4.1 one vs one策略
假设我们有N个类别,该策略基本思想就是不同类别两两之间训练一个分类器,这时我们一共会训练出 ��2 种不同的分类器。在预测时,我们将样本提交给所有的分类器,一共会获得N(N - 1)个结果,最终结果通过投票产生。
4.2 one vs all策略
该策略基本思想就是将第i中类型的所有样本作为正例,将剩下的所有样本作为负例,进行训练得到一个分类器。这样我们就一共可以得到N个分类器。在预测时,我们将样本提交给所有的分类器,一共会获得N个结果,我们选择其中概率值最大的那个作为最终分类结果。

4.3 softmax
softmax是LR在多分类的推广。与LR一样,同属于广义线性模型。什么是Softmax函数?假设我们有一个数组A, �� 表示的是数组A中第i个元素,那么这个元素的softmx值就是
��=���∑����
也就是说,是该元素的指数,与所有元素指数的比值。那么softmax模型的假设函数又是怎样的呢?

由上式很明显可以得出,假设函数的分母其实就是对概率分布进行了归一化,使得所有类别的概率之和为1;也可以看出LR其实就是K=2的softmax。在参数获得上,我们可以采用one vs all策略获得K个不同的训练数据集进行训练,进而针对每一类别都会得到一组参数向量 � .当测试样本特征向量x输入时,我们先用假设函数针对每一个类别j估计出概率值P(y=j|x)。因此我们的假设函数将要输出一个K维的向量(向量元素和为1)来表示K个类别的估计概率,我们选择其中得分最大的类别作为该输入的预测类别。softmax看起来和one vs all的LR很像,它们最大的不同在于softmax得到的K个类别的得分和为1,而one vs all的LR并不是。
- softmax的损失函数

- 多分类与LR
有了多分类的处理方法,那么我们什么时候该用多分类LR?什么时候用softmax呢?
总的来说,若待分类的类别互斥,我们就使用softmax方法,若待分类的类别有相交,我们则要选用多分类LR,然后投票表决。
五、LR特点以及适用场景


最后一些知识点补充

问题1 逻辑回归是线性模型吗?
逻辑回归的模型引入了sigmoid函数映射,是非线性模型,但本质上又是一个线性回归模型,因为除去sigmoid映射函数关系,其他的步骤,算法都是线性回归的。可以说,逻辑回归,都是以线性回归为理论支持的。
这里讲到的线性,是说模型关于系数 � 一定是线性形式的,

加入sigmoid映射后,变成:

如果分类平面本身就是线性的,那么逻辑回归关于特征变量x,以及关于系数�都是线性的。
如果分类平面是非线性的,例如 �12+�2=0 ,那么逻辑斯蒂回归关于变量x是非线性的,但是关于参数�仍然是线性的。

这里,我们做了一个关于变量x的变换: ,�0′=�0,�1′=�12,�2′=�2
其他非线性超平面一样的道理,我们可以通过变量的变化,最终一定可以化成形如

的东西,我们把z看作�的变量,就是个线性模型。剩下的工作,无非是去构造映射关系

综上,逻辑回归本质上是线性回归模型,关于系数是线性函数,分离平面无论是线性还是非线性的,逻辑回归其实都可以进行分类。对于非线性的,需要自己去定义一个非线性映射。
问题2:请从最大似然的角度去解释逻辑回归,以及逻辑回归的损失函数是什么?
假设对于输入x分类为1和0的概率分别为:

则概率函数为:

假设样本数据有m个,并且独立,则它们的联合分布可以由各边际分布的乘积表示,则由似然函数为:

取对数似然函数:

化简:

为了求解最优的参数θ,则需要最大化上述的对数似然函数,而上述的对数似然函数是以和的形式展示的,取负号,并乘以一个常数项,问题则变为求解最小值,转化如下:
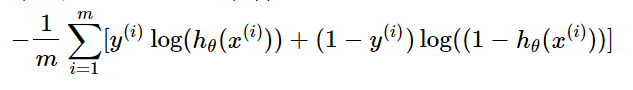
就是逻辑回归的损失函数。