树——算法专项刷题（八）

八、树

主要是对二叉树的前、中、后、层序遍历的应用
（这四种遍历详见二叉树遍历）

8.1二叉树的最近公共祖先

原题链接

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
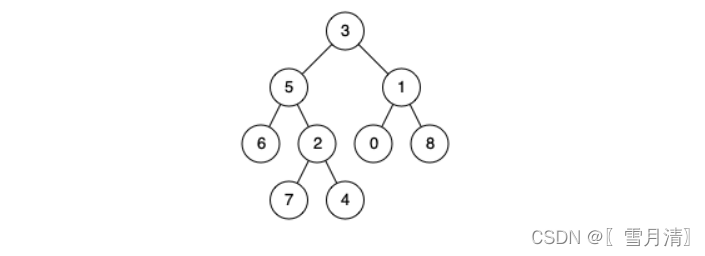
在这里插入图片描述

示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

思路： 分三种情况

p和q分布在左右子树，最近公共祖先就是root
p和q分布在同一侧，最近公共祖先就是不为空的一侧（left or right）
p和q有至少一个就是root或者root为null ，最近公共祖先就是root

注意点： 递归root的左右子树，根据情况返回对应的公共祖先结点

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        

        if(root == null || p == root || q == root){
            return root;
        }

        //查左子树

        TreeNode l = lowestCommonAncestor(root.left,p,q);

        // 查右子树

        TreeNode r = lowestCommonAncestor(root.right,p,q);

//公共祖先在右子树
        if(l == null){
            return r;
        }

       else if(r == null){
           // 在左子树
        return l;
        }else{
            // 左右都不为空
            return root;
        }



    }
}

8.2从根节点到叶结点的路径数字之和

原题链接

给定一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的所有数字之和。

叶节点 是指没有子节点的节点。
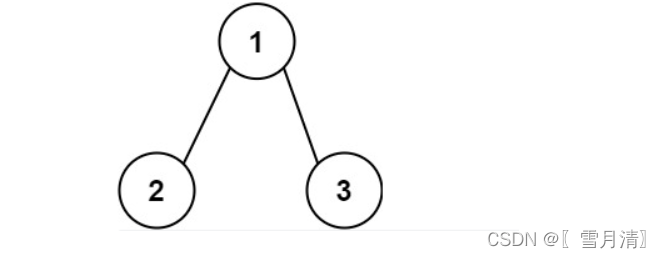
在这里插入图片描述

示例 1：

输入： root = [1,2,3]

输出： 25

解释：

从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

思路： 先序递归遍历，如果遇到叶子结点就进行计数

注意点： 叶子结点才进行求和操作

class Solution {
    int num = 0;
    public int sumNumbers(TreeNode root) {
        
        sum(root,0);

        return num;

    }

    void sum(TreeNode root, int val){

        if(root == null){
             
              return;
        }

      val= val*10 + root.val;

      if(root.left == null && root.right == null){
          num += val;
      }

      sum(root.left,val);
      sum(root.right,val);


    }
}

8.3二叉树剪枝

原题链接

给定一个二叉树根节点 root ，树的每个节点的值要么是 0，要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。

节点 node 的子树为 node 本身，以及所有 node 的后代。

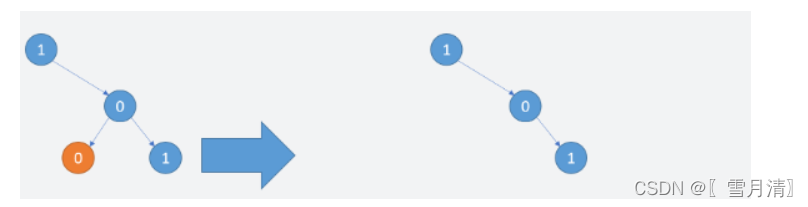
示例 1:

输入: [1,null,0,0,1]
输出: [1,null,0,null,1]
解释:

只有红色节点满足条件“所有不包含 1 的子树”。

右图为返回的答案。

思路： 递归遍历每一个节点，如果一个节点的值为0就返回一个true，然后对所有返回true的节点置为NULL

注意点： 以递归函数返回的状态值判断是否进行剪枝操作

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode pruneTree(TreeNode root) {
  if(dfs(root))  root = null;

  return root;


    }

    boolean dfs(TreeNode root){
        if(root == null) return false;
        if(dfs(root.left)){
            root.left = null;
        }

        if(dfs(root.right)){
            root.right = null;
        }

        if(root.left == null && root.right == null && root.val == 0){
            return true;
        }
        return false;
    }
}

8.4序列化与反序列化二叉树

原题链接

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

示例 1：
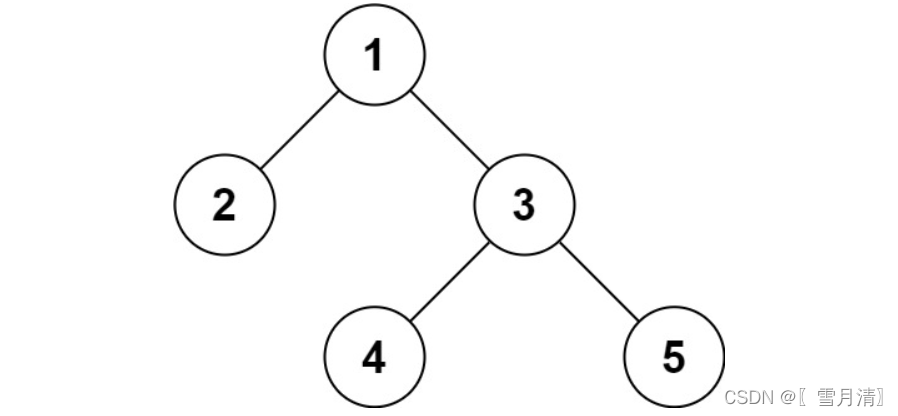
在这里插入图片描述

输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

提示：

树中结点数在范围 [0, 10^4] 内
-1000 <= Node.val <= 1000

思路： 前序遍历二叉树，将二叉树每个节点的值拼接为字符串，空树使用#表示

注意点： 在反序列化时，通过分割,将字符串转为数组

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {

        return rserialize(root,"");

    }

       // 1,2,#,#,3,4,#,#,5,#,#,
    public String rserialize(TreeNode root,String str){
     
        // 空子树使用 #代替
        if(root == null){
            str += "#,";
        }else{
            str += String.valueOf(root.val) + ",";
            str = rserialize(root.left,str);
            str = rserialize(root.right,str);
        }
        return str;
    }
    
    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {

         // 以逗号进行分割
         String[] split = data.split(",");

        List<String> list =  new LinkedList<String>( Arrays.asList(split));
           
        return rdeserialize(list);
    }

    public TreeNode rdeserialize(List<String> list) {
        // 空树
        if(list.get(0).equals("#")){
            list.remove(0);
            return  null;
        }
        // 反序列化
        
            TreeNode root = new TreeNode(Integer.valueOf(list.get(0)));
        list.remove(0);
        root.left = rdeserialize(list);
        root.right = rdeserialize(list);
        
        return root;
    }
}

8.5向下的路径节点之和

原题链接

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

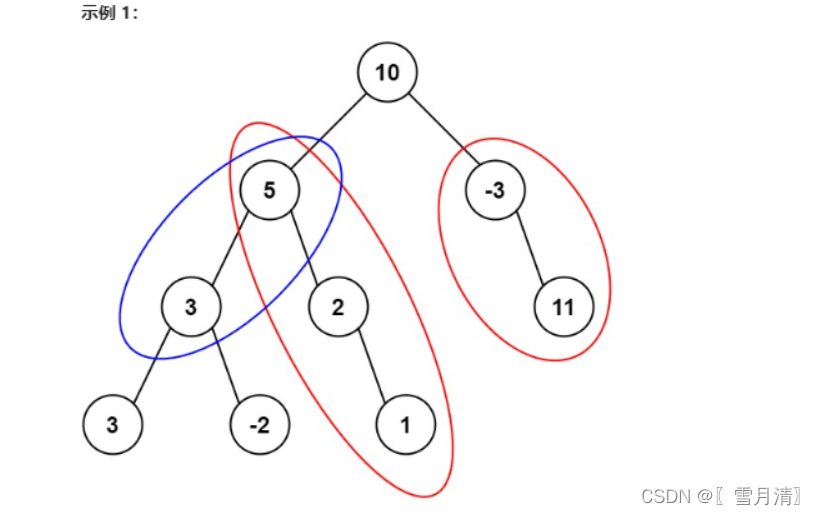
在这里插入图片描述

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

提示:

二叉树的节点个数的范围是 [0,1000]
-10^9 <= Node.val <= 10^9
-1000 <= targetSum <= 1000

解法一：

思路： 对每个结点递归遍历，每次用当前节点值和target 比较，若相等说明找到了一条路径，若不等就用target - 当前节点值，继续遍历左右子树

注意点： 考虑出现溢出的情况，使用long统计和

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int sum = 0;
    public int pathSum(TreeNode root, int targetSum) {

     if(root == null) return 0;
      
      dfs(root,targetSum);
      pathSum(root.left,targetSum);
      pathSum(root.right,targetSum);

return sum;

    }

    void dfs(TreeNode node, long target){
      
      if(node == null ) return;
      if(node.val == target) sum++;
     
      
      dfs(node.left,target - node.val);
      dfs(node.right,target - node.val);

    }
}

解法二：前缀和

思路： 使用map记录前缀和 -> 出现次数，遍历一个节点，检查map中是否存在遍历过的路径和 - targetSum ，存在几个这样的数值就说明存在几条符合条件的路径

注意点： 在遍历其他子树时，需要删除之前遍历另一条路径时map中记录的值

class Solution {
    public int pathSum(TreeNode root, int targetSum) {
        Map<Long,Integer> map = new HashMap<>();

        map.put(0l,1);

return dfs(root,map,0l,targetSum);



    }

    private int dfs(TreeNode root, Map<Long, Integer> map, long cur, int targetSum) {
        
        if(root == null) return 0;
        int res = 0;
        cur += root.val;
        
        res = map.getOrDefault(cur - targetSum,0);
        map.put(cur,map.getOrDefault(cur,0)+1);
        res += dfs(root.left,map,cur,targetSum);
        res += dfs(root.right,map,cur,targetSum);
        
        // 回溯
        map.put(cur,map.getOrDefault(cur,0) -1);
        
        return res;


    }


}

8.6节点之和最大的路径

原题链接

路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和是路径中各节点值的总和。

给定一个二叉树的根节点 root ，返回其最大路径和，即所有路径上节点值之和的最大值。

示例 1：

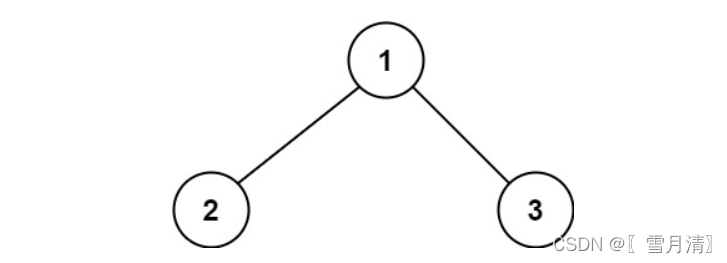
在这里插入图片描述

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

提示：

树中节点数目范围是 [1, 3 * 10^4]
-1000 <= Node.val <= 1000

思路：当前节点为 null 返回0，不为null 记录当前节点左子树最大路径和 +右子树最大路径和 + 当前节点值与 sum 作比较，表示最大路径和。而对于每个节点求该节点左右子树两条路径的最大值 + 该节点值表示该节点的贡献值

注意点：求左右子树最大值时，注意只有大于0才加入到路径和

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int sum = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
           dfs(root);

           return sum;
       

    }

    int dfs(TreeNode root){
       

         if(root == null) return 0;
         
         int left = Math.max(dfs(root.left),0);
         int right = Math.max(dfs(root.right),0);
         
         sum = Math.max(sum,left + right + root.val);

         // 返回当前节点左右两条路径的最大值
       return Math.max(left,right) + root.val;



    }
}

8.7展平二叉搜索树

原题链接

给你一棵二叉搜索树，请 按中序遍历 将其重新排列为一棵递增顺序搜索树，使树中最左边的节点成为树的根节点，并且每个节点没有左子节点，只有一个右子节点。

示例 1：
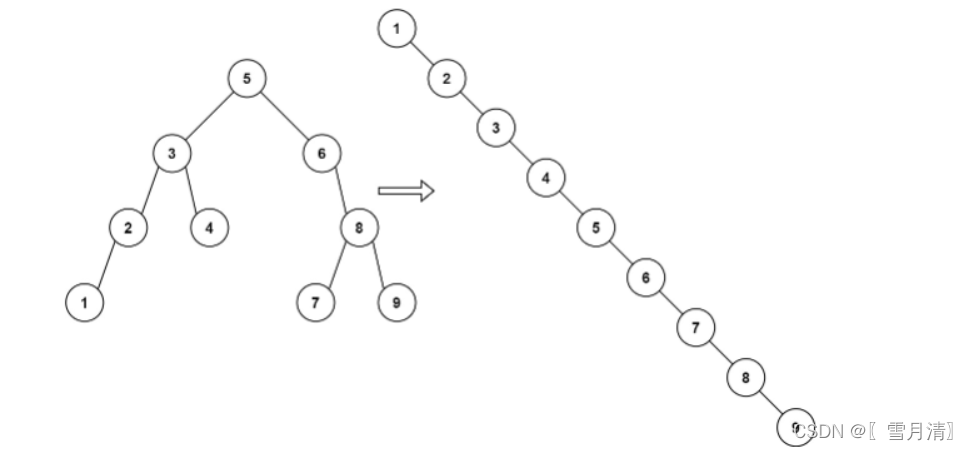
在这里插入图片描述

输入：root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
输出：[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

提示：

树中节点数的取值范围是 [1, 100]
0 <= Node.val <= 1000

思路： 中序遍历，使用list集合记录中序遍历的结果，然后进行重新构建树

注意点： 重新构建时需要重新创建节点

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer>list = new ArrayList();
    public TreeNode increasingBST(TreeNode root) {
   if(root == null) return null;

   dfs(root);
   TreeNode head = new TreeNode(-1);
   TreeNode p = head;
  for(int val : list){
      TreeNode temp = new TreeNode(val);
        p.right = temp;
        p = temp;
  }

return head.right;

    }

    void dfs(TreeNode node){

        if(node == null ) return;
        dfs(node.left);
        list.add(node.val);
        dfs(node.right);

    }

}

8.8二叉搜索树中的中序后继

原题链接

给定一棵二叉搜索树和其中的一个节点 p ，找到该节点在树中的中序后继。如果节点没有中序后继，请返回 null 。

节点 p 的后继是值比 p.val 大的节点中键值最小的节点，即按中序遍历的顺序节点 p 的下一个节点。

示例 1：

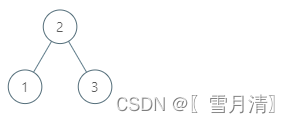
在这里插入图片描述

输入：root = [2,1,3], p = 1
输出：2
解释：这里 1 的中序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。

提示：

树中节点的数目在范围 [1, 10^4] 内。
-10^5 <= Node.val <= 10^5
树中各节点的值均保证唯一。

思路： 利用二叉搜索树的特性

注意点： 当前节点＞ p.val 需要记录一下这个节点

class Solution {
   
    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
          
   
   if(root == null) return null;
   TreeNode node = null;

   while( root != null){
       if(root.val > p.val){
           // 记录后一个
           node = root;

           root = root.left;
       }else{
           root = root.right;
       }
   }

   return node;


    }

}

8.9所有大于等于节点的值之和

原题链接

给定一个二叉搜索树，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

提示：

树中的节点数介于 0 和 10^4 之间。
每个节点的值介于 -10^4 和 10^4 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。

示例 1：

输入：root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

思路： 逆向中序遍历

class Solution {
    int sum = 0;
    public TreeNode convertBST(TreeNode root) {

          if(root == null) return root;


          convertBST(root.right);
          root.val+=sum;
          sum = root.val;
          convertBST(root.left);

          return root;
    }
}

8.10 二叉搜索树迭代器

实现一个二叉搜索树迭代器类BSTIterator ，表示一个按中序遍历二叉搜索树（BST）的迭代器：

BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字，且该数字小于 BST 中的任何元素。
boolean hasNext() 如果向指针右侧遍历存在数字，则返回 true ；否则返回 false 。
int next()将指针向右移动，然后返回指针处的数字。

注意，指针初始化为一个不存在于 BST 中的数字，所以对 next() 的首次调用将返回 BST 中的最小元素。

可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 的中序遍历中至少存在一个下一个数字。

示例：

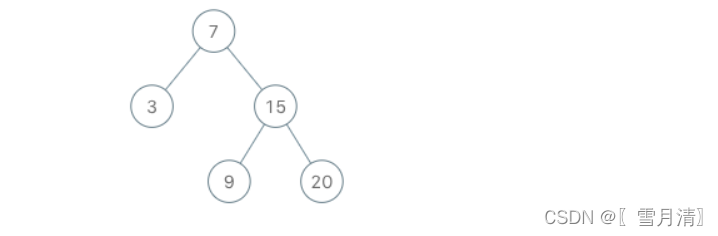
在这里插入图片描述

输入：

inputs = [“BSTIterator”, “next”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”]
inputs = [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]

输出:

[null, 3, 7, true, 9, true, 15, true, 20, false]

解释:

BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // 返回 3
bSTIterator.next(); // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 20
bSTIterator.hasNext(); // 返回 False

提示：

树中节点的数目在范围 [1, 105] 内
0 <= Node.val <= 106
最多调用 105 次 hasNext 和 next 操作

思路： 简单中序遍历，使用list集合存入遍历的节点值

class BSTIterator {

    List<Integer> list;
    int idx ;
    
    public BSTIterator(TreeNode root) {
      
        list = new ArrayList<>();
        idx = 0;
        dfs(root);

    }

    private void dfs(TreeNode root) {
        if(root == null) return;
        dfs(root.left);
        list.add(root.val);
        dfs(root.right);
    }

    public int next() {
     return list.get(idx++);

    }

    public boolean hasNext() {
   if(idx < list.size()) return  true;
   return false;

    }
}

8.11 二叉搜索树中两个节点之和

给定一个二叉搜索树的 根节点 root 和一个整数 k , 请判断该二叉搜索树中是否存在两个节点它们的值之和等于 k 。假设二叉搜索树中节点的值均唯一。

示例 1：

输入: root = [8,6,10,5,7,9,11], k = 12
输出: true
解释: 节点 5 和节点 7 之和等于 12

提示：

二叉树的节点个数的范围是 [1, 10^4].
-10^4 <= Node.val <= 10^4
root 为二叉搜索树
-10^5 <= k <= 10^5

思路： set集合+深度优先遍历

class Solution {
    Set<Integer> set = new HashSet<>();
    public boolean findTarget(TreeNode root, int k) {
            
            if(root == null) return false;

            if(set.contains(k - root.val)) return true;

            set.add(root.val);


           return findTarget(root.left,k) || findTarget(root.right,k);

            
    }

  
}

8.12值和下标之差都在给定的范围内

给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j，使得 abs(nums[i] - nums[j]) <= t ，同时又满足 abs(i - j) <= k 。

如果存在则返回 true，不存在返回 false。

示例 1：

输入：nums = [1,2,3,1], k = 3, t = 0
输出：true
提示：
0 <= nums.length <= 2 * 10^4
-2^31 <= nums[i] <= 2^31 - 1
0 <= k <= 10^4
0 <= t <= 2^31 - 1

思路： 使用TreeSet 树状集合，在集合中维护一个大小为k的窗口，保证集合中的数下标差的绝对值不大于k，遍历数组，对每个数查找集合中最接近的数，并判断两个数之差的绝对值不大于t

注意点： 将数组中的数都转为long型，防止溢出

class Solution {
  public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
        int n = nums.length;
        TreeSet<Long> ts = new TreeSet<>();
        for (int i = 0; i < n; i++) {
            Long u = nums[i] * 1L;
            // 从 ts 中找到小于等于 u 的最大值（小于等于 u 的最接近 u 的数）
            Long l = ts.floor(u); 
            // 从 ts 中找到大于等于 u 的最小值（大于等于 u 的最接近 u 的数）
            Long r = ts.ceiling(u); 
            if(l != null && u - l <= t) return true;
            if(r != null && r - u <= t) return true;
            // 将当前数加到 ts 中，并移除下标范围不在 [max(0, i - k), i) 的数（维持滑动窗口大小为 k）
            ts.add(u);
            if (i >= k) ts.remove(nums[i - k] * 1L);
        }
        return false;
  }
}

8.13 日程表

原题链接

请实现一个 MyCalendar 类来存放你的日程安排。如果要添加的时间内没有其他安排，则可以存储这个新的日程安排。

MyCalendar 有一个 book(int start, int end)方法。它意味着在 start 到 end 时间内增加一个日程安排，注意，这里的时间是半开区间，即 [start, end), 实数 x 的范围为， start <= x < end。

当两个日程安排有一些时间上的交叉时（例如两个日程安排都在同一时间内），就会产生重复预订。

每次调用 MyCalendar.book方法时，如果可以将日程安排成功添加到日历中而不会导致重复预订，返回 true。否则，返回 false 并且不要将该日程安排添加到日历中。

请按照以下步骤调用 MyCalendar 类: MyCalendar cal = new MyCalendar(); MyCalendar.book(start, end)

示例:

输入:

[“MyCalendar”,“book”,“book”,“book”]
[[],[10,20],[15,25],[20,30]]

输出: [null,true,false,true]

解释:

MyCalendar myCalendar = new MyCalendar();
MyCalendar.book(10, 20); // returns true
MyCalendar.book(15, 25); // returns false ，第二个日程安排不能添加到日历中，因为时间 15 已经被第一个日程安排预定了
MyCalendar.book(20, 30); // returns true ，第三个日程安排可以添加到日历中，因为第一个日程安排并不包含时间 20

提示：

每个测试用例，调用 MyCalendar.book 函数最多不超过 1000次。
0 <= start < end <= 10^9

思路： 使用TreeSet集合，实现自动排序和快速插入，需要自定义排序规则

注意点： 自定义排序规则

class MyCalendar {

    public static final class MySort implements Comparable<MySort>{
        private  int start;
        private  int end;
        //自定义排序规则
        public MySort(int start,int end){
            this.start = start;
            this.end = end;
        }
        

        @Override
        public int compareTo(MySort sort) {
            if(end <= sort.start){
                return  -1;
            }
            if(sort.end <= start){
                return  1;
            }
            return 0;
        }
    }
    TreeSet<MySort> set = new TreeSet<>();
    public MyCalendar() {

    }

    public boolean book(int start, int end) {

        return  set.add(new MySort(start,end));
        
    }
}