引言

上一节介绍了随机最大似然(Stochastic Maximum Likelihood)求解最优模型参数的过程。本节将介绍对比散度(Constractive Divergence,CD)。

回顾：随机最大似然求解模型参数的过程

针对极大似然估计，使用梯度上升算法使模型参数$\theta$逼近最优参数$\hat{\theta }$：
$$\begin{array}{r}\hat{\theta }=\underset{\theta }{\mathrm{argmax}}\log \prod _{i=1}^N\mathcal{P}(x^{(i)};\theta )\\ {\theta }^{(t+1)}\Leftarrow {\theta }^{(t)}+\eta {\nabla }_{\theta }\mathcal{L}(\theta )\end{array}$$

关于目标函数梯度${\nabla }_{\theta }\mathcal{L}(\theta )$表示如下：
$${\nabla }_{\theta }\mathcal{L}(\theta )={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};\theta )\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[{\nabla }_{\theta }\log \hat{\mathcal{P}}(\mathcal{X};\theta )\right]$$
其中：

• ${\mathcal{P}}_{data}$表示真实分布，该分布是客观存在的，可以将样本集合$\mathcal{X}$看作是从${\mathcal{P}}_{data}$中采出的$N$个样本；

• ${\mathcal{P}}_{model}$表示模型分布，它实际上是基于样本特征或者概率图结构假设出来的分布；

• ${\mathbb{E}}_{{\mathcal{P}}_{data}}\left[{\nabla }_{\theta }\log \hat{\mathcal{P}}(x^{(i)};\theta )\right]$表示正相(Positive Phase)，它本质上是基于${\mathcal{P}}_{data}$的期望结果。由于样本集合$\mathcal{X}$的特征均是可观测的，因而正相的期望求解更加简单。如：批梯度下降法(Batch Gradient Descent)；mini-Batch 梯度下降法等。

• ${\mathbb{E}}_{{\mathcal{P}}_{model}}\left[{\nabla }_{\theta }\log \hat{\mathcal{P}}(\mathcal{X};\theta )\right]$表示负相(Negative Phase)。负相难求解的原因在于：它不像${\mathcal{P}}_{data}$是恒定不变的，并拥有$\mathcal{X}$提供采样；我们假定的${\mathcal{P}}_{model}$要逼近${\mathcal{P}}_{data}$，但随着${\mathcal{P}}_{model}$分布的变化，我们对它中间过程的分布一无所知。

  因此，采用马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo Method)在梯度上升算法过程中，每一次迭代过程都需要对${\mathcal{P}}_{model}$进行采样，从而近似计算负相结果。

最终，通过正相、负相的计算结果，联合更新模型参数$\theta$的梯度方向，最终近似求解最优模型参数$\hat{\theta }$。

随机最大似然的缺陷

对于负相难求解问题，通常使用马尔可夫链蒙特卡洛方法进行分布近似，如吉布斯采样。根据吉布斯采样的要求，并不是直接从分布中采样出$\mathcal{M}$个样本，而是基于坐标上升思想将分布收敛成平稳分布(Stationary Distribution)后，从平稳分布中进行采样。
基于吉布斯采样初始分布到平稳分布的收敛过程表示如下：

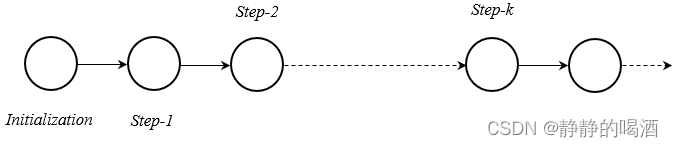
假设从$\text{Step-1}$开始，收敛至$\text{Step-k}$后达到平稳分布，从第$\text{q}(q>k)$次迭代中进行采样，直到采出$\mathcal{M}$个样本为止。
从初始状态收敛至平稳分布的过程称作‘混合时间’(Mixing Time).

回顾吉布斯采样的迭代过程，每一个$\text{Step}$的执行过程是复杂的：

• 需要基于每一维度进行采样，并且在采样过程中需要将其他所有维度固定(遍历过的、没遍历过的)；
• 直至所有维度均遍历一遍，一次$\text{Step}$才算完成。

这种迭代过程是十分消耗时间的，关于上述采样方法，容错率是极低的。因为如果没有收敛至平稳分布的话，那么一个样本都采不出来。
从而衍生出一种 以空间换时间 的采样方法，一次性使用若干条马尔可夫链进行采样。换句话说：哪条马尔可夫链达到平稳分布了，就从那条链中抽一个样本。这样采样容错率就很高，并且尽量满足每个样本均从不同的平稳分布中采样出来，保证了样本之间 相互独立：

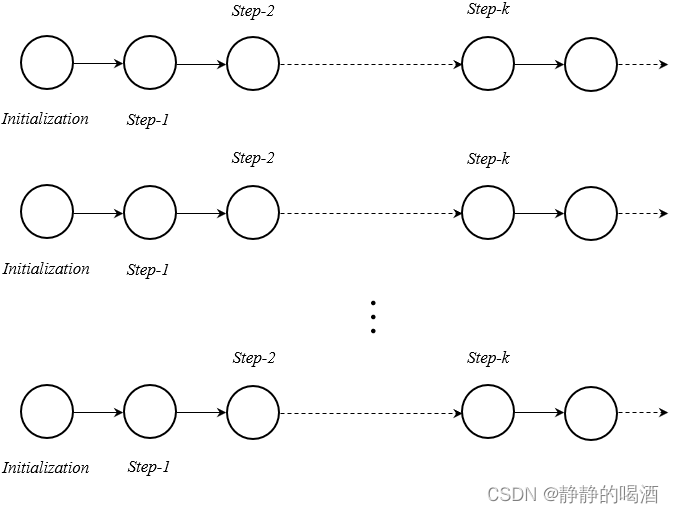
这种采样方式的弊端自然是消耗更多的存储资源。

吉布斯采样的缺陷与对比散度思想

即便是以空间换时间，这种采样结果可能依然很低效。其核心原因是：在每次吉布斯采样的初始$\text{Step}$中，需要给定一个初始分布；这个初始分布可以是任意分布，通常会设置为简单分布。如均匀分布、高斯分布等。但如果要近似的${\mathcal{P}}_{model}$分布过于复杂，导致吉布斯采样在迭代过程中混合时间很长，甚至是极难收敛至平稳分布。

如何处理这种难收敛的问题：对比散度(Constractive Divergence)这种方法从初始分布入手。初始分布本质上是从任意分布中采集的样本点，而对比散度的朴素思想是：与其从任意分布中进行采样，干脆直接采样一些优秀的样本点。

什么样的样本点是优秀的样本点？自然是这些样本点作为初始分布后，能够 更快地收敛至平稳分布。而这里的平稳分布指的自然是${\mathcal{P}}_{model}$。什么样的初始分布和${\mathcal{P}}_{model}$相似呢？对比散度的思路是：将正相中${\mathcal{P}}_{data}$采样的$\mathcal{M}$个样本点直接作为负相采样的初始分布。
既然要求解的${\mathcal{P}}_{model}$最终是要逼近${\mathcal{P}}_{data}$的，直接用${\mathcal{P}}_{data}$的样本，自然会加快${\mathcal{P}}_{model}$的逼近速度。

这种方法被称为$\text{CD-k}$，这里的$k$自然表示吉布斯采样的步骤编号。这种方法的特点在于：我们并非一定要达到平稳分布后再执行采样，仅仅通过若干次迭代之后，即便没有达到平稳分布，也可以进行采样。
$\text{CD-1}$表示从第一次迭代结束后，直接进行采样。以此类推。

感性理解：

• 基于CD的朴素思想，初始分布的样本点${\hat{x}}^{(i)}(i=1,2,\cdots ,\mathcal{M})\sim {\mathcal{P}}_{data}$,在收敛至平稳分布的迭代过程中，它的本质就是将${\mathcal{P}}_{data}\Rightarrow {\mathcal{P}}_{model}$方向上的过渡过程；在计算完梯度之后，最终还是要将${\mathcal{P}}_{model}\Rightarrow {\mathcal{P}}_{data}$方向逼近。莫不如一开始采集出的样本与${\mathcal{P}}_{data}$的关联度高，从而更快地将${\mathcal{P}}_{model}$分布向${\mathcal{P}}_{data}$分布方向‘牵引’。
• 相反地，并不是一开始的$\text{CD-0}$就一定是最优的分布，即便是使用${\mathcal{P}}_{data}$的采样结果作为初始分布，但依然需要‘在给定这些可见单元的隐藏单元条件分布上采样的马尔可夫链上进行[磨合]’(摘自《深度学习》(花书)373页).

对比散度名称的由来

从$\mathcal{K}\mathcal{L}$散度的角度描述极大似然估计

回顾基于归一化后概率模型$\mathcal{P}(\mathcal{X};\theta )$的极大似然估计：
加上一个系数$\frac{1}{N}$,并不影响最值的取值结果。
$$\begin{array}{rl}\hat{\theta }& =\underset{\theta }{\mathrm{argmax}}\log \prod _{i=1}^N\mathcal{P}(x^{(i)};\theta )\\ & =\underset{\theta }{\mathrm{argmax}}\frac{1}{N}\sum _{i=1}^N\log \mathcal{P}(x^{(i)};\theta )\end{array}$$
因而上述式子可写成期望形式：

• 再次强调，将 X = { x ( i ) } i = 1 N \mathcal X = \{x^{(i)}\}_{i=1}^N X={x(i)}i=1N​视作真实分布${\mathcal{P}}_{data}$中采集出的样本结果;而‘均值结果写作期望’在这里是蒙特卡洛方法的逆向表示。因为${\mathcal{P}}_{data}$确实是‘无法精确得到的分布’。即便写成了期望形式，并不影响最优参数的求解。
• 而$\mathcal{P}(x^{(i)};\theta )$实际上就是基于‘样本特征/概率图结构’假设的概率模型，因此将其写作${\mathcal{P}}_{model}(x^{(i)};\theta )$.
  $$\begin{array}{rl}& \\ & \frac{1}{N}\sum _{i=1}^N\log \mathcal{P}(x^{(i)};\theta )\approx {\mathbb{E}}_{{\mathcal{P}}_{data}}[\log \mathcal{P}(\mathcal{X};\theta )]\\ & \hat{\theta }=\underset{\theta }{\mathrm{argmax}}{\mathbb{E}}_{{\mathcal{P}}_{data}}\left[\log {\mathcal{P}}_{model}(\mathcal{X};\theta )\right]\end{array}$$

假设随机变量集合$\mathcal{X}$是连续型随机变量(观察方便起见)，将上述式子描述为积分形式：
${\mathcal{P}}_{data}$本身是客观存在的概率分布，和这里的模型参数$\theta$无关。
$$\hat{\theta }=\underset{\theta }{\mathrm{argmax}}{\int }_{\mathcal{X}}{\mathcal{P}}_{data}(\mathcal{X})\log {\mathcal{P}}_{model}(\mathcal{X};\theta )d\mathcal{X}$$

将上述式子执行如下变换：
在中括号中减去一个和$\theta$无关的常量——${\mathcal{P}}_{data}(\mathcal{X})\log {\mathcal{P}}_{data}(\mathcal{X})$,并不影响最优参数的求解
$$\begin{array}{rl}\hat{\theta }& =\underset{\theta }{\mathrm{argmax}}{\int }_{\mathcal{X}}\left[P_{data}(\mathcal{X})\log {\mathcal{P}}_{model}(\mathcal{X};\theta )-{\mathcal{P}}_{data}(\mathcal{X})\log {\mathcal{P}}_{data}(\mathcal{X})\right]d\mathcal{X}\\ & =\underset{\theta }{\mathrm{argmax}}{\int }_{\mathcal{X}}{\mathcal{P}}_{data}(\mathcal{X})\cdot \left[\log {\mathcal{P}}_{model}(\mathcal{X};\theta )-\log {\mathcal{P}}_{data}(\mathcal{X})\right]d\mathcal{X}\\ & =\underset{\theta }{\mathrm{argmax}}{\int }_{\mathcal{X}}{\mathcal{P}}_{data}(\mathcal{X})\cdot \log \left[\frac{{\mathcal{P}}_{model}(\mathcal{X};\theta )}{{\mathcal{P}}_{data}(\mathcal{X})}\right]d\mathcal{X}\end{array}$$
这明显是$\mathcal{K}\mathcal{L}$散度的表示格式：
KL散度在EM算法，变分推断中最早提到过，本质上是描述两分布之间关联程度的一个量。其结果非负恒成立，当两分布相等时，KL散度等于0.
θ ^ = arg ⁡ max ⁡ θ { − K L [ P d a t a ( X ) ∣ ∣ P m o d e l ( X ; θ ) ] } = arg ⁡ min ⁡ θ { K L [ P d a t a ( X ) ∣ ∣ P m o d e l ( X ; θ ) ] } \begin{aligned} \hat \theta & = \mathop{\arg\max}\limits_{\theta} \left\{-\mathcal K \mathcal L \left[\mathcal P_{data}(\mathcal X) || \mathcal P_{model}(\mathcal X;\theta)\right]\right\} \\ & = \mathop{\arg\min}\limits_{\theta} \left\{\mathcal K \mathcal L \left[\mathcal P_{data}(\mathcal X) || \mathcal P_{model}(\mathcal X;\theta)\right]\right\} \end{aligned} θ^​=θargmax​{−KL[Pdata​(X)∣∣Pmodel​(X;θ)]}=θargmin​{KL[Pdata​(X)∣∣Pmodel​(X;θ)]}​

这也是极大似然估计的另一角度逻辑：通过求解合适的模型参数$\hat{\theta }$，使得真实分布${\mathcal{P}}_{data}(\mathcal{X})$与模型学习分布${\mathcal{P}}_{model}(\mathcal{X};\theta )$之间的$\mathcal{K}\mathcal{L}$散度达到最小。
对原始基于概率模型$\mathcal{P}(\mathcal{X};\theta )$的描述更加精进一步————对概率模型进行更精进的划分，并描述两种概率模型之间的逻辑关系。

对比散度的本质

上述关于$\mathcal{K}\mathcal{L}$散度的描述适用于任意模型的极大似然估计。继续观察负相中的吉布斯采样过程：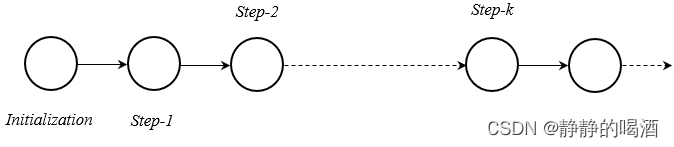
从对比散度思想的角度观察，初始化分布(Initialization)就是从${\mathcal{P}}_{data}$中采集的样本，这里 记作${\mathcal{P}}_0$(吉布斯采样第0步骤的分布结果)；而经过相当多次的迭代后，其分布结果是平稳分布，即当前时刻的${\mathcal{P}}_{model}$，这里 记作${\mathcal{P}}_{\infty }$(这里仅表示一个符号，$\infty$表示相当多次的迭代后达到平稳分布)。

关于极大似然估计，使用上述符号可表示为如下形式：
θ ^ = arg ⁡ min ⁡ θ { K L [ P d a t a ( X ) ∣ ∣ P m o d e l ( X ; θ ) ] } = arg ⁡ min ⁡ θ { K L [ P 0   ∣ ∣   P ∞ ] } \begin{aligned} \hat \theta & = \mathop{\arg\min}\limits_{\theta} \left\{\mathcal K \mathcal L \left[\mathcal P_{data}(\mathcal X) || \mathcal P_{model}(\mathcal X;\theta)\right]\right\} \\ & = \mathop{\arg\min}\limits_{\theta} \left\{\mathcal K\mathcal L [\mathcal P_0 \text{ }|| \text{ }\mathcal P_{\infty}]\right\} \end{aligned} θ^​=θargmin​{KL[Pdata​(X)∣∣Pmodel​(X;θ)]}=θargmin​{KL[P0​ ∣∣ P∞​]}​

同上，吉布斯采样的第1步，第2步,…,第$k$步骤等等也可以表示为${\mathcal{P}}_1,{\mathcal{P}}_2,\cdots ,{\mathcal{P}}_k,{\mathcal{P}}_{k+1},\cdots$

如果根据上述对比散度的思想：在吉布斯采样的第$k$步进行采样，即便第$k$步骤并不是平稳分布，这相当于 吉布斯采样只迭代了一部分，就直接进行采样使用了，此时的模型参数$\theta$的优化问题表示如下：
$$\hat{\theta }=\underset{\theta }{\mathrm{argmin}}\left[\mathcal{K}\mathcal{L}({\mathcal{P}}_0||{\mathcal{P}}_{\infty })-\mathcal{K}\mathcal{L}({\mathcal{P}}_k||{\mathcal{P}}_{\infty })\right]$$

个人理解：

• 可以将$\mathcal{K}\mathcal{L}({\mathcal{P}}_0||{\mathcal{P}}_{\infty })$看作是${\mathcal{P}}_{data},{\mathcal{P}}_{model}$之间‘总差距’的一种量的表示；同理，$\mathcal{K}\mathcal{L}({\mathcal{P}}_k||{\mathcal{P}}_{\infty })$表示吉布斯采样第k次迭代产生的分布${\mathcal{P}}_k$与${\mathcal{P}}_{model}$之间的差距。
• 和原始的极大似然估计相比，这种‘对比散度’方式对差距的范围描述明显更小了————将${\mathcal{P}}_k\to {\mathcal{P}}_{\infty }$的差距全部减掉了。
• 而减掉的这一部分对于整个差距来说，比重是很小的。因为在吉布斯采样的迭代过程中，最开始的几步一定是‘更新较大的’————随着步骤的增加，最终‘磨合’成平稳分布${\mathcal{P}}_{model}$。而更新较大的步骤能够带来较高的‘梯度’，从而使梯度上升过程中能够变化更快。

这里解释说明了《机器学习》(花书)P372页最下方的描述：“CD可以被理解为去掉了正确MCMC梯度更新中的最小项，这解释了偏差的由来。”

配分函数部分将介绍到这里，后续会将受限玻尔兹曼机的学习任务部分补上。

相关参考：
3-What is Contrastive Divergence(对比散度)
4-Name of Contrastive Divergence(对比散度名字的由来)
深度学习(花书)——第18章 直面配分函数