【算法】最长公共子序列编辑距离（两个序列之间的DP）

news2024/9/26 1:27:46

文章目录

  • 最长公共子序列（LCS）
  • 编辑距离（Edit Distance）
  • 总结
  • 相关题目练习
    • 583. 两个字符串的删除操作 https://leetcode.cn/problems/delete-operation-for-two-strings/
    • 712. 两个字符串的最小ASCII删除和 https://leetcode.cn/problems/minimum-ascii-delete-sum-for-two-strings/
      • 解法1：求编辑距离
      • 解法2：求最长子序列
    • 1458. 两个子序列的最大点积 https://leetcode.cn/problems/max-dot-product-of-two-subsequences/
    • 97. 交错字符串 https://leetcode.cn/problems/interleaving-string/

本文记录这种两个序列之间相互比较的 dp 题目的通用模板。

最长公共子序列（LCS）

1143. 最长公共子序列

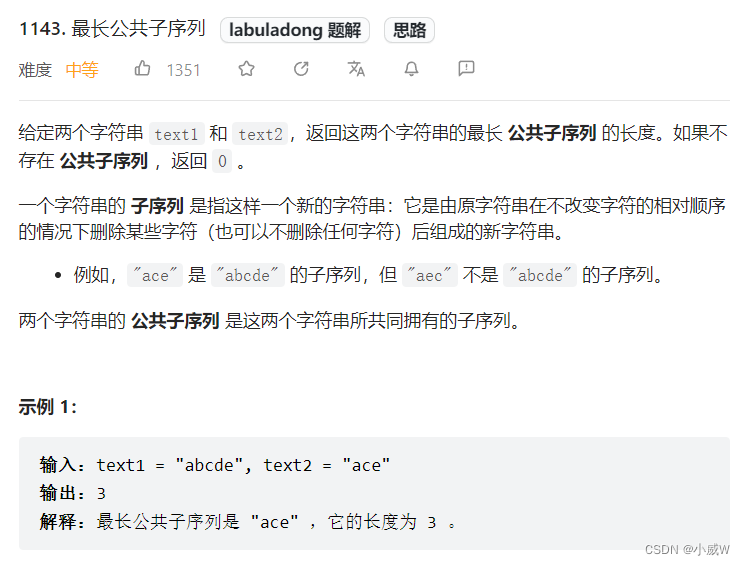
在这里插入图片描述
递推公式如下
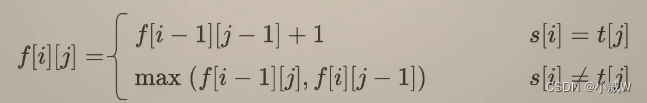
在这里插入图片描述
为了避免出现负数下标，因此定义 dp 数组时定义成 dp[m + 1][n + 1]。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length(), n = text2.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        return dp[m][n];
    }
}

可以优化成一维 dp 数组。

因为 dp[i][j] 的取值只和 左上角，上面 和 左边 这三个位置的数字有关，只需要引入一个额外的变量 pre 记录一下遍历过程中被覆盖的 dp[j]作为下一次左上角的值 就好了。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length(), n = text2.length();
        int[] dp = new int[n + 1];
        for (int i = 1; i <= m; ++i) {
            int pre = dp[0];
            for (int j = 1; j <= n; ++j) {
                int tmp = dp[j];
                dp[j] = text1.charAt(i - 1) == text2.charAt(j - 1)? pre + 1: Math.max(dp[j], dp[j - 1]);
                pre = tmp;
            }
        }
        return dp[n];
    }
}

编辑距离（Edit Distance）

72. 编辑距离

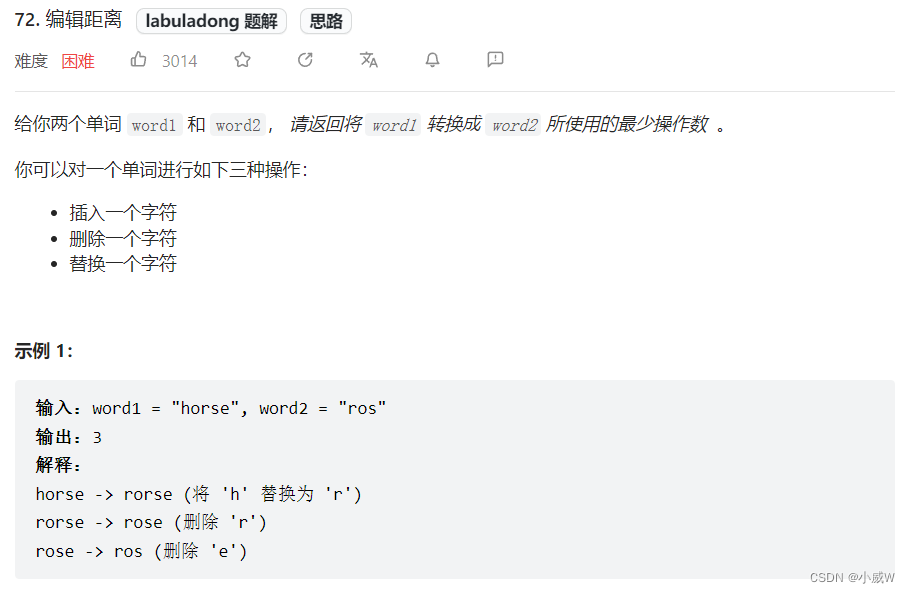
在这里插入图片描述
先定义 dp[i][j] 表示 word1 从0~i，word2 从0~j 需要的最少操作数。

递推公式如下：
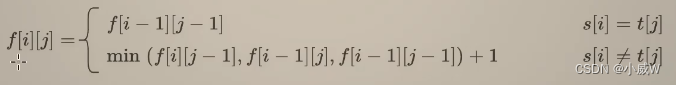
在这里插入图片描述
min() 中的三个 分别对应 删除、添加、替换 这三种操作。

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length(), n = word2.length();
        int[][] dp = new int[m + 1][n + 1];
        // dp数组初始化
        for (int i = 0; i <= m; ++i) dp[i][0] = i;
        for (int j = 0; j <= n; ++j) dp[0][j] = j;
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1];
                else dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
            }
        }
        return dp[m][n];
    }
}

继续优化成一维 dp 数组

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length(), n = word2.length();
        int[] dp = new int[n + 1];
        for (int j = 0; j <= n; ++j) dp[j] = j;
        for (int i = 1; i <= m; ++i) {
            dp[0] = i;				// 注意这里的dp[0]要随着i的变化更新
            int pre = dp[0] - 1;    // 引入额外的pre记录被覆盖的dp[i-1][j-1]
            for (int j = 1; j <= n; ++j) {
                int tmp = dp[j];
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) dp[j] = pre;
                else dp[j] = Math.min(pre, Math.min(dp[j], dp[j - 1])) + 1;
                pre = tmp;
            }
        }
        return dp[n];
    }
}

总结

这两道题目的类似点在于都是比较两个序列之间的内容，这种情况下通常定义 dp 数组为：
dp[m + 1][n + 1] （之所以 + 1 是为了方式遍历的过程中出现负数下标）

与之对应，遍历元素的时候，使用的下标分别是 i - 1 和 j - 1。（因为原始数据的数据范围还是 0 ~ m 和 0~ n）

由于无后效性，即 dp[i][j] 的数值只与和它接近的几个数字有关，因此可以优化 dp 数组的空间。

相关题目练习

583. 两个字符串的删除操作 https://leetcode.cn/problems/delete-operation-for-two-strings/

https://leetcode.cn/problems/delete-operation-for-two-strings/
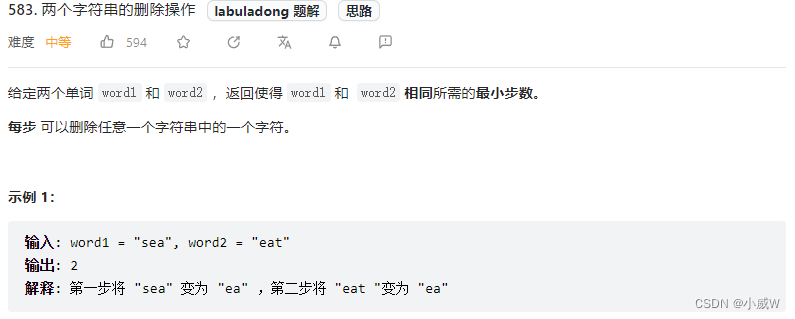
在这里插入图片描述
和 72. 编辑距离 这道题目很像，唯一的区别在于，可以使用的操作只有删除任意一个字符串中的一个元素。

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length(), n = word2.length();
        int[][] dp = new int[m + 1][n + 1];
        // dp数组初始化
        for (int i = 0; i <= m; ++i) dp[i][0] = i;
        for (int j = 0; j <= n; ++j) dp[0][j] = j;
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1];
                else dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
            }
        }
        return dp[m][n];
    }
}

直接把 72. 编辑距离 这道题目的答案复制过来，删除 dp[i - 1][j - 1] 到 dp[i][j] 的转移即可（对应着这道题没有替换元素的操作）

712. 两个字符串的最小ASCII删除和 https://leetcode.cn/problems/minimum-ascii-delete-sum-for-two-strings/

https://leetcode.cn/problems/minimum-ascii-delete-sum-for-two-strings/

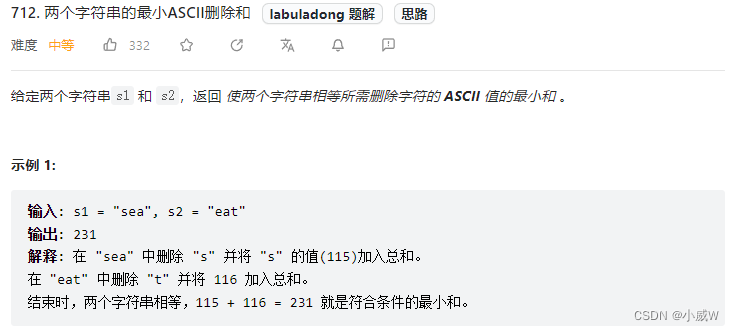
在这里插入图片描述

解法1：求编辑距离

同样是只有删除操作的编辑距离，除此之外，每次操作需要的花费变成了字符的 ASCII 码。

class Solution {
    public int minimumDeleteSum(String s1, String s2) {
        int m = s1.length(), n = s2.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; ++i) dp[i][0] = dp[i - 1][0] + s1.charAt(i - 1);
        for (int j = 1; j <= n; ++j) dp[0][j] = dp[0][j - 1] + s2.charAt(j - 1);
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                char a = s1.charAt(i - 1), b = s2.charAt(j - 1);
                if (a == b) dp[i][j] = dp[i - 1][j - 1];
                else dp[i][j] = Math.min(dp[i - 1][j] + a, dp[i][j - 1] + b);
            }
        }
        return dp[m][n];
    }
}

解法2：求最长子序列

这一题乍一看和上一题很像！ 但其实应该反过来想，这道题求的也可以是最长公共子序列，这样剩下的就是需要被删除的字符了。

class Solution {
    public int minimumDeleteSum(String s1, String s2) {
        int m = s1.length(), n = s2.length(), sum = 0;
        int[][] dp = new int[m + 1][n + 1];
        for (char ch: s1.toCharArray()) sum += ch;
        for (char ch: s2.toCharArray()) sum += ch;
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                char a = s1.charAt(i - 1), b = s2.charAt(j - 1);
                if (a == b) dp[i][j] = dp[i - 1][j - 1] + a + b;
                else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        return sum - dp[m][n];
    }
}

1458. 两个子序列的最大点积 https://leetcode.cn/problems/max-dot-product-of-two-subsequences/

https://leetcode.cn/problems/max-dot-product-of-two-subsequences/

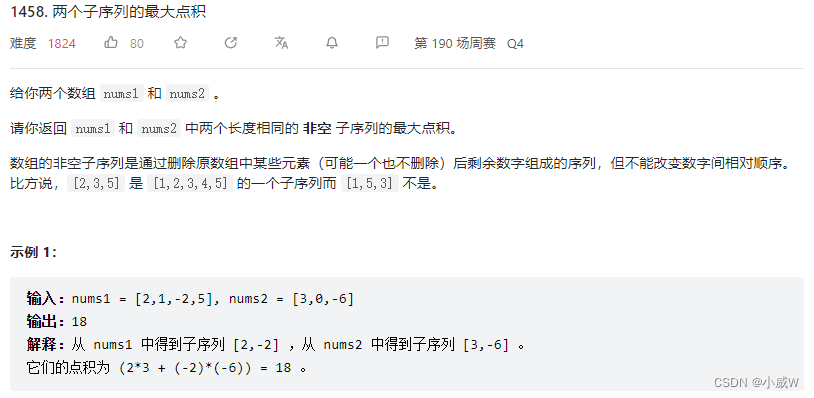
在这里插入图片描述
这道题目有两点需要注意，子序列要求：1.长度相同 2.非空。

这道题目一开始写成了：

class Solution {
    public int maxDotProduct(int[] nums1, int[] nums2) {
        int m = nums1.length, n = nums2.length;
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                int v = nums1[i - 1] * nums2[j - 1];
                dp[i][j] = Math.max(v + dp[i - 1][j - 1], dp[i][j]);
            }
        }
        return dp[m][n];
    }   
}

结果发现答案要求是非空的，也就是如果只有负数的话，那没办法，负数也得选进去。

正解如下：

class Solution {
    public int maxDotProduct(int[] nums1, int[] nums2) {
        int m = nums1.length, n = nums2.length;
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 0; i <= m; ++i) Arrays.fill(dp[i], Integer.MIN_VALUE / 2);	// 因为负数也得选，就先都设成一个比较小的数字
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                dp[i][j] = nums1[i - 1] * nums2[j - 1]; // 至少也得选一个
                dp[i][j] = Math.max(Math.max(dp[i - 1][j], dp[i][j - 1]), dp[i][j]);
                dp[i][j] = Math.max(nums1[i - 1] * nums2[j - 1] + dp[i - 1][j - 1], dp[i][j]);
            }
        }
        return dp[m][n];
    }
}

这道题目做起来手感怪怪的。

97. 交错字符串 https://leetcode.cn/problems/interleaving-string/

https://leetcode.cn/problems/interleaving-string/
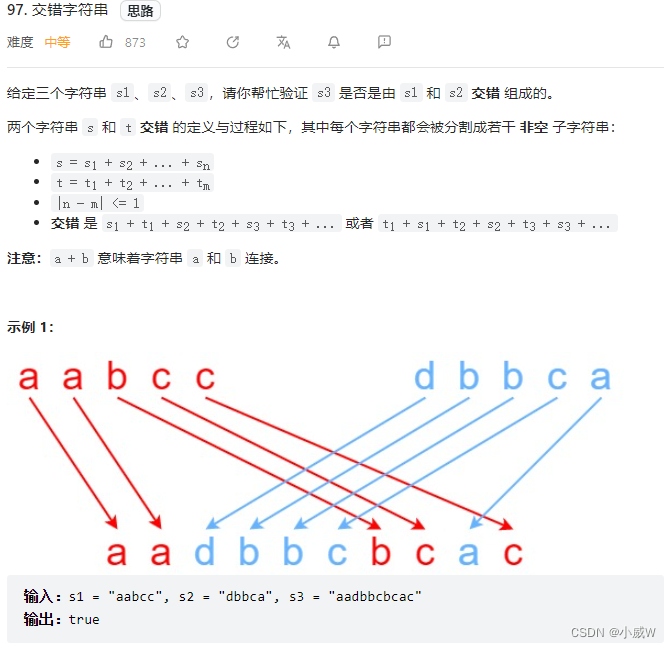
在这里插入图片描述
dp[i][j] 表示 s1 的前 i 个元素 和 s2 的前 j 个元素 能否组成 s3 的前 i + j 个元素。

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int m = s1.length(), n = s2.length(), t = s3.length();
        if (m + n != t) return false;
        boolean[][] dp = new boolean[m + 1][n + 1];     // 表示能组合成的序列长度
        dp[0][0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                if (i > 0 && s1.charAt(i - 1) == s3.charAt(i + j - 1)) dp[i][j] |= dp[i - 1][j];
                if (j > 0 && s2.charAt(j - 1) == s3.charAt(i + j - 1)) dp[i][j] |= dp[i][j - 1];
            }
        }
        return dp[m][n];
    }
}

注意这个时候 i 和 j 的 for 循环的起始点都是 0 而不是 1 了。

关于 s3 的下标为什么是 i + j - 1。举个例子，当 i = 1, j = 1,此时对应的两个下标都是0，那么这两个合起来之后对应 s3 的下标是 i + j - 2 和 i + j - 1。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/709807.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

BWA序列比对方法丨针对较大基因组的并行计算和性能优化方式，利用多线程和负载均衡策略提高效率

BWA序列比对方法丨针对较大基因组的并行计算和性能优化方式，利用多线程和负载均衡策略提高效率

BWA 序列比对 高通量测序技术日新月异发展迅猛&#xff0c;产生了数亿级大数据&#xff0c;生命的世界由DNA序列ATCG组成&#xff0c;正如计算机的世界由二进制01组成。 高通量测序的工作实质是把一本生命字典撕成碎片&#xff0c;然后每人手里拿一片&#xff0c;招募成千上万…
阅读更多...
【洛谷】B3644 【模板】拓扑排序 / 家谱树（用邻接表存储和其他题解不一样哦）

【洛谷】B3644 【模板】拓扑排序 / 家谱树（用邻接表存储和其他题解不一样哦）

本薅蒻通过这次学到的知识点&#xff08;本人认为好用的东西&#xff09;&#xff1a; 1&#xff1a; &#xff08;情况适用于输入的x为0时结束输入&#xff09; 2&#xff1a; 先输出“t”(就是因为这里wa了好几发&#xff0c;555555) 原本是在 if里面输出的&#xff0c;这…
阅读更多...
mysql通过存储过程解决ERROR 1060 (42S21): Duplicate column的问题

mysql通过存储过程解决ERROR 1060 (42S21): Duplicate column的问题

问题描述 实际的日常开发工作中&#xff0c;经常需要对现有表的结构作出变更&#xff0c;涉及到sql相关的操作&#xff0c;基本都通过初始化脚本来完成&#xff0c;如果初始化脚本运行失败或者遇到其他问题&#xff0c;可能导致sql部分执行&#xff0c;不分失败的问题&#xf…
阅读更多...
ModaHub ——向量数据库Milvus特征向量和预写式日志教程

ModaHub ——向量数据库Milvus特征向量和预写式日志教程

目录 特征向量 什么是特征向量 特征向量的优势 应用领域 预写式日志 数据可靠性 缓冲区设置 旧日志删除 特征向量 什么是特征向量 向量是具有一定大小和方向的量&#xff0c;可以简单理解为一串数字的集合&#xff0c;就像一行多列的矩阵&#xff0c;比如&#xff1a…
阅读更多...
领域事件驱动（三）子域

领域事件驱动（三）子域

上一章对领域层的相关概念做了阐述 应用服务 应用层作为展现层与领域层的桥梁&#xff0c;是用来表达用例和用户故事的主要手段。 应用层通过应用服务接口来暴露系统的全部功能。在应用服务的实现中&#xff0c;它负责编排和转发&#xff0c;它将要实现的功能委托给一个或多…
阅读更多...
蓝桥杯刷题-1

蓝桥杯刷题-1

文章目录 1.蓝桥杯官网2.蓝桥杯题目进入界面 及 题目详情3.题目解答过程及思路4.运行结果图5.解答代码展示6.ASCII表图例 大家好&#xff0c;我是晓星航。今天为大家带来的是 蓝桥杯刷题 - 1 -单词分析 相关的讲解&#xff01;&#x1f600; 1.蓝桥杯官网 题库 - 蓝桥云课 (l…
阅读更多...
source insight小键盘在vim中不能使用数字(数字按键变英文)

source insight小键盘在vim中不能使用数字(数字按键变英文)

文章目录 问题描述解决办法注意&#xff1a; 问题描述 在使用source insight登录远程服务器并使用vim编辑模式时&#xff0c;出现数字键盘的0-9变成了yxwvutsrqp情况。 解决办法 注意&#xff1a; 如果你点了save as…的话&#xff0c;会让你保存untitled.key文件到你指定的路…
阅读更多...
Redis保姆级安装(windows版)

Redis保姆级安装(windows版)

MySQL是一种传统的关系型数据库&#xff0c;我们可以使用MySQL来很好的组织跟管理我们的数据 但是MySQL的缺点也是很明显的&#xff01;他的数据始终是存在硬盘里的&#xff0c;对于我们的用户的信息经常不修改的内容用MySQL存储的确可以&#xff0c;但是如果要快速更新或者是频…
阅读更多...
Excel的一些操作：移动列，添加索引

Excel的一些操作：移动列，添加索引

移动列 在 Excel 中移动列的 5 种方法——分步教程 选中某一列&#xff0c;然后鼠标放在边缘&#xff0c;移动到你想移动到的列 添加索引 例如&#xff0c;我想添加的索引列名为“index”&#xff0c;然后选中想要添加序列的行&#xff0c;点击“填充-->录入123序列”
阅读更多...
顶部导航菜单组件的一种做法

顶部导航菜单组件的一种做法

今天来分享一款顶部导航的菜单做法&#xff0c;可以参考一下。 它的效果是这个样子的。虽然不算太好看&#xff0c;但是也能实现具体功能 &#xff0c;剩了不少时间。 废话不多说&#xff0c;直接上代码。 以下是html代码。 <!DOCTYPE html PUBLIC "-//W3C//DTD XHT…
阅读更多...
【Spring】Bean的作用域与生命周期详情：请简述Spring的执行流程并分析Bean的生命周期？

【Spring】Bean的作用域与生命周期详情：请简述Spring的执行流程并分析Bean的生命周期？

前言 我们都知道&#xff0c;Spring框架为开发人员提供了很多便捷&#xff0c;这使得开发人员能够更加专注于应用程序的核心业务逻辑&#xff0c;而不需要花费大量时间和精力在技术细节上。作为一个包含众多工具方法的IoC容器&#xff0c;存取JavaBean是其极为重要的一个环节。…
阅读更多...
vue + leaflet实现图标指定方向随机旋转

vue + leaflet实现图标指定方向随机旋转

效果 github地址 官方示例Demo 安装leaflet-rotatedmarker npm install leaflet-rotatedmarker -S引入leaflet.rotatedmarker import leaflet-rotatedmarker实现 this.laryerGroup this.$L.layerGroup() data.forEach(item > {this.layerGroup.addLayer(this.getMarke…
阅读更多...
【tomcat知识点和部署】

【tomcat知识点和部署】

文章目录 一、tomcat概述1.1 tomcat的介绍1.2 tomcat的特点 二、tomcat核心组件2.核心组件的介绍2.1 Web容器2.2 servlet容器2.3 JSP容器2.4 Tomcat核心组件的请求方式&#xff08;交互方式&#xff09;2.4.1 Web容器2.4.2 JSP容器2.4.3 serverlet容器2.5 Tomcat处理请求&#…
阅读更多...
第六章 linux调试器——gdb的使用

第六章 linux调试器——gdb的使用

第六章 linux调试器——gdb的使用 一、前提1、debug与release2、gdb的安装 二、常用调试指令1、开始调试2、代码显示3、断点设置4、代码执行5、信息监控6、退出调试 一、前提 1、debug与release 程序最终的发布方式分成两种&#xff0c;一种是debug模式&#xff0c;一种是rel…
阅读更多...
华为OD机试真题 Python 实现【机器人活动区域】【2023Q1 200分】

华为OD机试真题 Python 实现【机器人活动区域】【2023Q1 200分】

目录 一、题目描述二、输入描述三、输出描述四、解题思路五、Python算法源码六、效果展示1、输入2、输出 一、题目描述 现有一个机器人&#xff0c;可放置于 M N的网格中任意位置&#xff0c;每个网格包含一个非负整数编号。当相邻网格的数字编号差值的绝对值小于等于 1 时&a…
阅读更多...
redis-单节点安装

redis-单节点安装

daemonize yes port 6379 bind 0.0.0.0 requirepass 123456 save 3600 1 300 100 60 10000dir /usr/local/redis dbfilename dump.rdb logfile redis.log pidfile redis.pid##save 3600 1 300 100 60 10000 ##3600秒(一小时),至少有一个值的话,会进行存盘 ##300秒(五分钟),至少…
阅读更多...
探索性测试: 工具和方法的综合应用

探索性测试: 工具和方法的综合应用

1、前言 2、工具的使用 1、测试管理工具 2、缺陷跟踪工具 3、测试自动化工具 4、探索性测试工具 5、代码覆盖率工具 6、日志分析工具 7、网络抓包工具 8、数据库查询工具 9、并发和负载测试工具 10、安全测试工具 11、API测试工具 12、数据生成工具 13、异常处理和边界测试工具…
阅读更多...
server2012远程桌面RDP120过期后修改

server2012远程桌面RDP120过期后修改

运行regedit 进入 HKEY_LOCAL_MACHINE \ SYSTEM \ CurrentControlSet \ Control \ Terminal Server \ RCM \ GracePeriod &#xff0c;选中 GracePeriod 重启电脑Ok
阅读更多...
572. 另一棵树的子树

572. 另一棵树的子树

另一棵树的子树 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, leftNone, rightNone): # self.val val # self.left left # self.right right class Solution:def isSubtree(self, root: Optional[Tre…
阅读更多...
ROS 编码器转Odom

ROS 编码器转Odom

双轮差速模型 移动距离 delta_dist (encoder_right encoder_left)/linesNum * circumference / 2; 旋转角度 Delta_th (float)(encoder_right - encoder_left) / wheel_track; 将移动距离转换到车体坐标系 delta_x cos(delta_th) * delta_dist; delta_y -sin(delta_th) * …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023