(02)Cartographer源码无死角解析-(67) 2D后端优化→FastCorrelativeScanMatcher2D -分支定界算法(BranchAndBound)1

讲解关于slam一系列文章汇总链接:史上最全slam从零开始，针对于本栏目讲解(02)Cartographer源码无死角解析-链接如下:
(02)Cartographer源码无死角解析- (00)目录_最新无死角讲解：https://blog.csdn.net/weixin_43013761/article/details/127350885

${\color{blue}{文末正下方中心}提供了本人 \color{red} 联系方式，\color{blue}点击本人照片即可显示WX→官方认证}$

一、前言

在上一篇博客中对 PrecomputationGrid 与 PrecomputationGridStack2D进行了纤细分析，其主要作用是用于构建多分辨率低，且在最后我们提到，存储在 PrecomputationGridStack2D 中层级越高的，则表示其分辨率约粗。该篇博客主要的目的就是实现如下：
在这里插入图片描述由图1、图2、图3 估算出机器人(节点在) 图gt 的位姿。这里假设 .lua 文件中的参数 branch_and_bound_depth=3为例进行讲解。其上的图1、图2、图3 看作上篇博客求解出来的多分辨率地图。

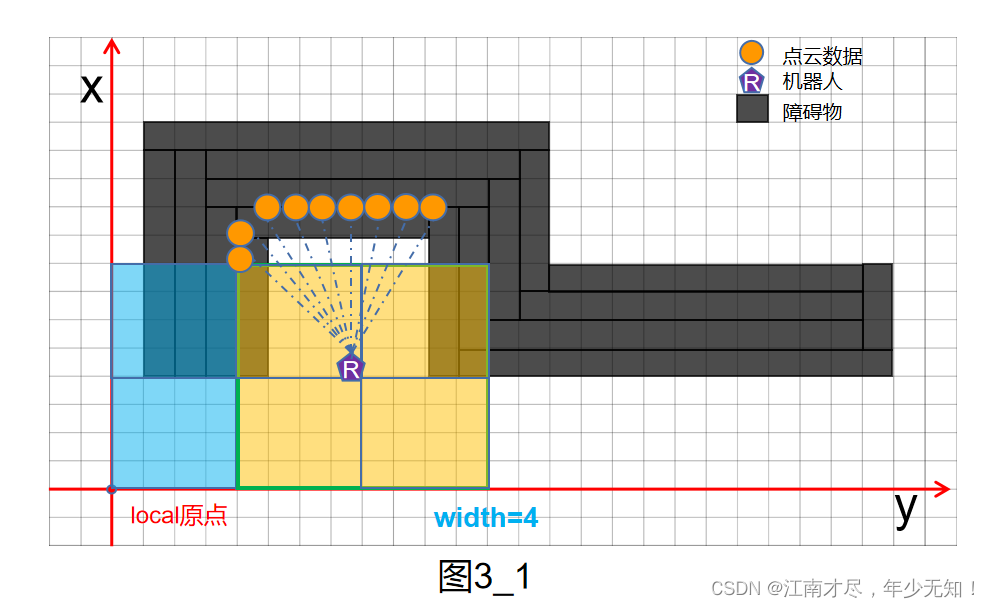
如图3所示，首先使用最最粗的分辨率，其中机器人的位姿认为是一个初始位姿，这里记为 $\mathbf {Robot3}^{local}_{tracking}$ ，很明显，基于这种比较粗的分辨率地图，是很容易匹配上的，但是很不精准。因为其对应的 width=4，如下图所示，4x4个像素会作为1个像素来对待，如下图所示，本人只绘画了一部分，也就是蓝色与黄色区域：
在这里插入图片描述
接下来就要 $\color{red}注意：$ 可以看到，机器人位姿落在 local 系下黄色区域，在[(0,1),(0,2),(1,1),(1,2)] 这4点处(从0开始)，进行暴力相关性扫描匹配，都能得到不错的优解，我们记为最优候选界，接下来，那么我们找到图2中的对应区域，需要注意，图2的 width=2，所以其会把 2x2=4 个像素作为1个像素来对待，如下：
在这里插入图片描述
首先对上诉中的[2:5,0:3]，也就是绿色矩形框内区域进行暴力相关性扫描匹配，最终找到四个候选解，也就是黄色区域，4点坐标分别为[(2,2),(2,3),(3,2),(3,3)] 。同理，再在图一中找到这四个点对应的区域，再进行暴力相关性扫描匹配，如下：
在这里插入图片描述
通过绿色矩形框内区域的暴力相关性扫描匹配，最终又可以求得四个不错的解，不过这次我们可以直接选取最高的那一个。也就是最终解。上图中的最优解与最前面的图gt 的解是十分接近的。

这里使用图示的方式进行讲解，虽然比较容易理解，但是不太好与树、枝、树深度、分支等名词联系起来。等分析完源码之后，我们再以树状的形式比体现一下，大家就明白怎么回事，为什么这个算法叫分支定界算法了。

二、::FastCorrelativeScanMatcher2D()

文件 fast_correlative_scan_matcher_2d.h 中可以看到 FastCorrelativeScanMatcher2D 类的声名，其成员变量十分的的简单，所以跳过了，直接从 FastCorrelativeScanMatcher2D 的构造函数讲起，不过其构造函数也是十分的简单，如下所示：

// 构造函数
FastCorrelativeScanMatcher2D::FastCorrelativeScanMatcher2D(
    const Grid2D& grid,
    const proto::FastCorrelativeScanMatcherOptions2D& options)
    : options_(options),
      limits_(grid.limits()),
      // 多分辨率地图的构建
      precomputation_grid_stack_(
          absl::make_unique<PrecomputationGridStack2D>(grid, options)) {}

其就是根据参数配置以及 grid 构建了一个多分辨率地图，即 PrecomputationGridStack2D 实例对象赋值给 precomputation_grid_stack_。

三、 ::Match() 与 SearchParameters

该函数主要调用了 MatchWithSearchParameters() 这个函数，如下：

/**
 * @brief 进行局部搜索窗口的约束计算(对局部子图进行回环检测)
 * 
 * @param[in] initial_pose_estimate 先验位姿
 * @param[in] point_cloud 原点位于local坐标系原点处的点云
 * @param[in] min_score 最小阈值, 低于这个分数会返回失败
 * @param[out] score 匹配后的得分
 * @param[out] pose_estimate 匹配后得到的位姿
 * @return true 匹配成功, 反之匹配失败
 */
bool FastCorrelativeScanMatcher2D::Match(
    const transform::Rigid2d& initial_pose_estimate,
    const sensor::PointCloud& point_cloud, const float min_score, float* score,
    transform::Rigid2d* pose_estimate) const {
  // param: linear_search_window angular_search_window 
  const SearchParameters search_parameters(options_.linear_search_window(),
                                           options_.angular_search_window(),
                                           point_cloud, limits_.resolution());
  return MatchWithSearchParameters(search_parameters, initial_pose_estimate,
                                   point_cloud, min_score, score,
                                   pose_estimate);
}

首先 initial_pose_estimate 表示机器人(节点的)初始位姿，或者说是待优化位姿。point_cloud 应该是 local 系下的点云数据。min_score 是一个阈值，后续计算出来的位姿解，只要得分大于该阈值，都看作是一个最有候选解。关于 SearchParameters 这个类，再前面有十分纤细的介绍，如下链接。

(02)Cartographer源码无死角解析-(49) 2D点云扫描匹配→相关性暴力匹配1：SearchParameters

该类中有几个函数是比较重要的，分别就是 SearchParameters ::GenerateRotatedScans() 与 DiscretizeScans()，作用分别是对地图上角度与位置上的遍历。另外还有 SearchParameters::ShrinkToFit() 这个函数。其再前面的博客种由于没有使用到，并没有进行分析，现在来看一下：

// 计算每一帧点云 在保证最后一个点能在地图范围内时 的最大移动范围
void SearchParameters::ShrinkToFit(const std::vector<DiscreteScan2D>& scans,
                                   const CellLimits& cell_limits) {
  CHECK_EQ(scans.size(), num_scans);
  CHECK_EQ(linear_bounds.size(), num_scans);

  // 遍历生成的旋转后的很多scan
  for (int i = 0; i != num_scans; ++i) {
    Eigen::Array2i min_bound = Eigen::Array2i::Zero();
    Eigen::Array2i max_bound = Eigen::Array2i::Zero();

    // 对点云的每一个点进行遍历, 确定这帧点云的最大最小的坐标索引
    for (const Eigen::Array2i& xy_index : scans[i]) {
      // Array2i.min的作用是 获取对应元素的最小值组成新的Array2i
      min_bound = min_bound.min(-xy_index);
      max_bound = max_bound.max(Eigen::Array2i(cell_limits.num_x_cells - 1,
                                               cell_limits.num_y_cells - 1) -
                                xy_index);
    }

    // 计算每一帧点云 在保证最后一个点能在地图范围内时 的最大移动范围
    linear_bounds[i].min_x = std::max(linear_bounds[i].min_x, min_bound.x());
    linear_bounds[i].max_x = std::min(linear_bounds[i].max_x, max_bound.x());
    linear_bounds[i].min_y = std::max(linear_bounds[i].min_y, min_bound.y());
    linear_bounds[i].max_y = std::min(linear_bounds[i].max_y, max_bound.y());
  }
}

scans 中包含了多帧点云数据，该函数会遍历每一帧点云，然后判断一帧点云在地图中能够朝4个方向移动的最大距离，按照该距离移动点云数据之后，保证至少有一个点云数据位于地图之后，否则就没有意义了，遍历的时候点云都跑到地图外面去了。

::Match() 函数在构建完 SearchParameters 实例 search_parameters之后，接着调用了 ::MatchWithSearchParameters() 函数，且把 search_parameters 作为实参传入。

四、::MatchWithSearchParameters()

$\color{blue}（1）：$ 从名字不难看出，该函数就是根据 SearchParameters 对象进行扫描匹配。首先来看该函数的输入：

// 进行基于分支定界算法的粗匹配
bool FastCorrelativeScanMatcher2D::MatchWithSearchParameters(
    SearchParameters search_parameters,
    const transform::Rigid2d& initial_pose_estimate,
    const sensor::PointCloud& point_cloud, float min_score, float* score,
    transform::Rigid2d* pose_estimate) const {
  CHECK(score != nullptr);
  CHECK(pose_estimate != nullptr);

该函数接受一个 SearchParameters 实例对象，以及一个初始位姿 initial_pose_estimate，同时还有进行暴力搜索的点云数据，这里的点云数据应该还是居于 local 系的，另外 min_score 用于过滤一些比好的位姿解。score 与 pose_estimate 分别用于存储匹配之后的分值与位姿。

$\color{blue}（2）：$ 接着就是对点云数据进行了一个旋转，点云的角度是相对于机器人(节点)坐标系了。然后在调用 GenerateRotatedScans 函数生成各个需要遍历角度的点云数据，本质上也是对点云数据进行旋转。

  // Step: 将原点处的点云先旋转到预测的方向上
  const Eigen::Rotation2Dd initial_rotation = initial_pose_estimate.rotation();
  const sensor::PointCloud rotated_point_cloud = sensor::TransformPointCloud(
      point_cloud,
      transform::Rigid3f::Rotation(Eigen::AngleAxisf(
          initial_rotation.cast<float>().angle(), Eigen::Vector3f::UnitZ())));

  // Step: 生成按照不同角度旋转后的点云集合
  const std::vector<sensor::PointCloud> rotated_scans =
      GenerateRotatedScans(rotated_point_cloud, search_parameters);

$\color{blue}（3）：$ 将旋转后的点云帧集合进行平移，平移之后的点云数据此时无论旋转还是平移都是相对于机器人(节点)坐标系了。然后或者这些点云数据在地图上的索引，如下

  // Step: 将旋转后的点云集合按照预测出的平移量进行平移, 获取平移后的点在地图中的索引
  // 这里的离散激光点是在最细的分辨率的地图上面
  const std::vector<DiscreteScan2D> discrete_scans = DiscretizeScans(
      limits_, rotated_scans,
      Eigen::Translation2f(initial_pose_estimate.translation().x(),
                           initial_pose_estimate.translation().y()));
  
  // 缩小搜索窗口的大小, 计算每一帧点云在保证最后一个点能在地图范围内时的最大移动范围
  search_parameters.ShrinkToFit(discrete_scans, limits_.cell_limits());

接着调用 search_parameters.ShrinkToFit() 函数，计算每一帧点云在保证最后一个点能在地图范围内时的最大移动范围，search_parameters.linear_bounds变量中。

$\color{blue}（4）：$ 记者就是调用 ComputeLowestResolutionCandidates() 函数获得分辨率最低(障碍物最粗)地图的所有合格的候选解，具体的细节稍后再讨论。

  // 计算最低分辨率中的所有的候选解 最低分辨率是通过搜索树的层数、地图的分辨率计算出来的.
  // 对于地图坐标系来说 最低分辨率=1<<h, h表示搜索树的总的层数
  // 这里不但对最低分辨率的所有候选解的得分进行了计算, 同时还按照从大到小排列
  const std::vector<Candidate2D> lowest_resolution_candidates =
      ComputeLowestResolutionCandidates(discrete_scans, search_parameters);

$\color{blue}（5）：$ 由了最初的一批候选解之后，就可以调用分支定界算法了，也就是BranchAndBound() 函数，代码如下所示：

  // Step: 进行基于分支定界算法的搜索, 获取最优解
  const Candidate2D best_candidate = BranchAndBound(
      discrete_scans, search_parameters, lowest_resolution_candidates,
      precomputation_grid_stack_->max_depth(), min_score); // param: max_depth
  
  // 检查最优解的值, 如果大于指定阈值min_score就认为匹配成功,否则认为不匹配返回失败
  if (best_candidate.score > min_score) {
    *score = best_candidate.score;
    // Step: 根据计算出的偏移量对位姿进行校准
    *pose_estimate = transform::Rigid2d(
        {initial_pose_estimate.translation().x() + best_candidate.x,
         initial_pose_estimate.translation().y() + best_candidate.y},
        initial_rotation * Eigen::Rotation2Dd(best_candidate.orientation));
    return true;
  }

对于 BranchAndBound() 暂时也不做详细分析，后续单独讲解。最后再判断一下最优的解是否超过指定阈值 min_score，如果超过，则对 initial_pose_estimate 进行调整，获得最有位姿。

五、::ComputeLowestResolutionCandidates()

现在回过头来分析代码 ComputeLowestResolutionCandidates。该代码其实也比较好理解，前面提到，源码中最低分辨率的地图：

precomputation_grids_[6]       width=64      可以简单理解，比原始地图构建的分辨率地图
增加x,y增加64-1=1个像素，且每 64x64=4096 个像素的像素值都用他们中最大的来代替(略有区别)

把 4096 个像素当作一个新像素来对待，且是对一个子图进行处理，那即使对子图的所有新像素方式进行遍历，也不会消耗多少资源，来看源码如下：

// 生成最低分辨率层(栅格最粗)上的所有候选解, 并进行打分与排序
std::vector<Candidate2D>
FastCorrelativeScanMatcher2D::ComputeLowestResolutionCandidates(
    const std::vector<DiscreteScan2D>& discrete_scans,
    const SearchParameters& search_parameters) const {

  // 生成最低分辨率层(栅格最粗)上的所有候选解
  std::vector<Candidate2D> lowest_resolution_candidates =
      GenerateLowestResolutionCandidates(search_parameters);

  // 计算每个候选解的得分, 按照匹配得分从大到小排序, 返回排列好的candidates 
  ScoreCandidates(
      precomputation_grid_stack_->Get(precomputation_grid_stack_->max_depth()),
      discrete_scans, search_parameters, &lowest_resolution_candidates);
  return lowest_resolution_candidates;
}

看起来逻辑是十分简单的，先调用 GenerateLowestResolutionCandidates() 函数根据 search_parameters 在前面调用 search_parameters.ShrinkToFit() 计算处出来，点云数据在在地图中移动的最大距离求得所有相关的候选解。然后通过 ScoreCandidates() 函数按降序方式排列。关于 GenerateLowestResolutionCandidates() 函数的代码不是很复杂，如下：

// 生成最低分辨率层(栅格最粗)上的所有候选解
std::vector<Candidate2D>
FastCorrelativeScanMatcher2D::GenerateLowestResolutionCandidates(
    const SearchParameters& search_parameters) const {
  const int linear_step_size = 1 << precomputation_grid_stack_->max_depth();
  int num_candidates = 0;
  // 遍历旋转后的每个点云
  for (int scan_index = 0; scan_index != search_parameters.num_scans;
       ++scan_index) {

    // X方向候选解的个数
    const int num_lowest_resolution_linear_x_candidates =
        (search_parameters.linear_bounds[scan_index].max_x -
         search_parameters.linear_bounds[scan_index].min_x + linear_step_size) /
        linear_step_size;

    // Y方向候选解的个数
    const int num_lowest_resolution_linear_y_candidates =
        (search_parameters.linear_bounds[scan_index].max_y -
         search_parameters.linear_bounds[scan_index].min_y + linear_step_size) /
        linear_step_size;

    // num_candidates 为最低分辨率这一层中所有候选解的总个数
    num_candidates += num_lowest_resolution_linear_x_candidates *
                      num_lowest_resolution_linear_y_candidates;
  }

  // 将所有候选解保存起来, 候选解的结构为（角度的索引, x偏移量, y偏移量, 搜索参数）
  std::vector<Candidate2D> candidates;
  candidates.reserve(num_candidates);

  for (int scan_index = 0; scan_index != search_parameters.num_scans;
       ++scan_index) {
    for (int x_index_offset = search_parameters.linear_bounds[scan_index].min_x;
         x_index_offset <= search_parameters.linear_bounds[scan_index].max_x;
         x_index_offset += linear_step_size) {
      for (int y_index_offset =
               search_parameters.linear_bounds[scan_index].min_y;
           y_index_offset <= search_parameters.linear_bounds[scan_index].max_y;
           y_index_offset += linear_step_size) {
        // 生成候选解, 存的是候选解与原始点云原点坐标间的偏移量
        candidates.emplace_back(scan_index, x_index_offset, y_index_offset,
                                search_parameters);
      }
    }
  }
  CHECK_EQ(candidates.size(), num_candidates);
  return candidates;
}

其首先循环遍历点云，这里简单理解为角度的遍历。循环过程中，有一个参数，那么就是 linear_step_size，这里就是等价于前面提到的 width=64，也就是 64x64=4096 作为一个像素来对待。遍历的过程中，使用到了 search_parameters.linear_bounds，遍历的每帧点云都要属于自己的 linear_bound，这样能保证所有的候选解点云帧至少有一个点云在地图中。

随后的操作需要注意一下，候选解存储的是相对于初始点云(机器人系)原点坐标间的偏移量，并不是一个绝对坐标。

六、结语

该篇博客通过首先通过图示，形象且直观的展示分支定界算法核心原理，且在后续过程中讲解了最低分辨率求得候选解的过程，且对候选者解进行降序排列。但是关于分支定界最核心的算法部分，即 FastCorrelativeScanMatcher2D::BranchAndBound() 暂未讲解，这就是下篇博客的主要内容了。