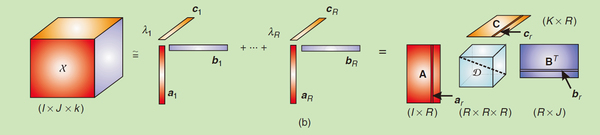
CP分解图示:
Tucker分解图示:

两者的区别如下:
-
主要区别:核张量(core tensor)
Tucker分解的结果会形成一个核张量,即PCA中的主成分因子,来表示原张量的主要性质,而CP分解没有核张量。 -
Tensor分解是n-秩与低秩近似,而CP分解是秩与低秩近似
在CP分解时我们都是先固定秩的个数,再去迭代,即没有用到张量本身的秩;但是在Tucker分解时我们是根据张量本身的秩进行分解的。 -
Tucker分解的唯一性不能保证
对于固定的n nn-秩,Tucker分解的唯一性不能保证,一般加上一些约束,如分解得到的因子单位正交约束等。CP分解的求解首先要确定分解的秩1张量的个数,通常我们通过迭代的方法对R RR从1开始遍历直到找到一个合适的解。 -
可加约束的共性
在一些应用中,为了使得CP分解更加的鲁棒和精确,可以在分解出的因子上加上一些先验知识即约束。比如说平滑约束(smooth)、正交约束、非负约束(nonegative) 、稀疏约束(sparsity)等。
除了可以在Tucker分解的各个因子矩阵上加上正交约束以外,还可以加一些其它约束,比如稀疏约束,平滑约束,非负约束等。另外在一些应用的场景中不同的mode的物理意义不同,可以加上不同的约束。 -
应用领域不同
Tucker分解可以看作是一个PCA的多线性版本,因此可以用于数据降维,特征提取,张量子空间学习等。比如说一个低秩的张量近似可以做一些去噪的操作等。Tucker分解同时在高光谱图像中也有所应用,如用低秩Tucker分解做高光谱图像的去噪,用张量子空间做高光谱图像的特征选择,用Tucker分解做数据的压缩等。
CP分解已经在信号处理,视频处理,语音处理,计算机视觉、机器学习等领域得到了广泛的应用。