C语言实现二叉搜索树BST

news2024/10/6 20:25:09

文章目录

- 初始化
- 搜索节点
- 删除节点

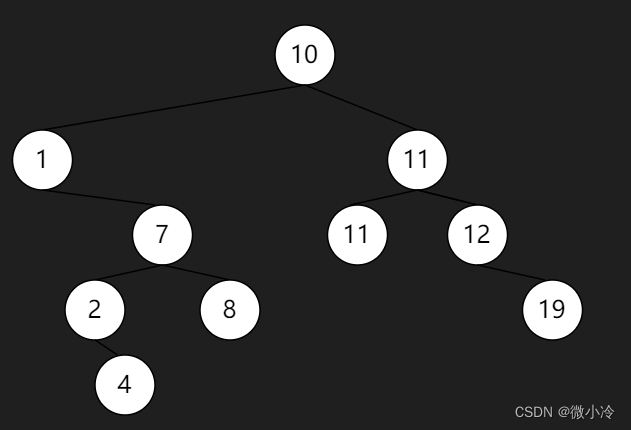
二叉搜索树(Binary Search Tree, BST)要求父节点大于等于其左子节点，而小于等于其右子节点，这样递归类推，相当于父节点大于等于其左侧的所有节点而小于等于右侧的所有节点，如下图所示

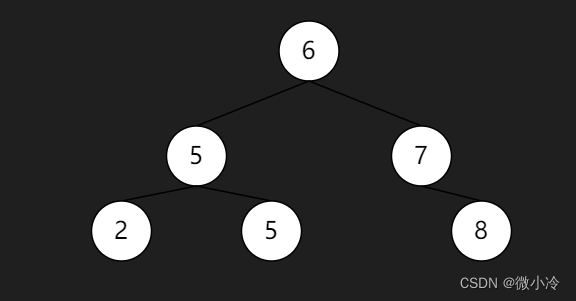
根据BST的规则，搜索时只需比较父子节点，故而最坏的情况也无非是查询到叶节点，此时比较次数为树的高度。作为二叉树，元素个数为 $n$ ，则树高不大于 $log_2n$ 。

初始化

在BST中，任一非根非叶的元素，需要有三个指针，分别指向父节点、左子节点和右子节点。而根节点没有父节点，叶节点没有子节点。C语言实现为

//bst.c
typedef struct TREENODE
{
    struct TREENODE *father;
    struct TREENODE *left;
    struct TREENODE *right;
    int value;
}tNode;

生成BST的第一步就是建立一个根节点，然后不断插入新节点。

插入新节点时，要和当前节点作比较，若新节点大于当前节点，则以其右子节点作为当前节点，继续比较；否则比较左子节点，直到当前节点为叶节点，正好可以把新节点插进来。

void insertNode(tNode* root, int val){
    tNode* new = (tNode*)malloc(sizeof(tNode));
    new->value=val;
    new->left=NULL;
    new->right=NULL;
    while (TRUE){
        if (root->value<val) 
            // 若右子节点存在，则将其置为root，并继续比较
            if(root->right!=NULL)
                root=root->right;
            else{
                //若右子节点不存在，则新节点成为其右子节点
                new->father = root;
                root->right = new;
                return;         //赋值之后函数结束
            }
        else                    //左边的操作与右边相同
            if (root->left!=NULL)
                root=root->left;
            else{
                new->father=root;
                root->left=new;
                return;
            }
    }
}

接下来，检验一下BST是否正确，把所有节点打印出来

//打印二叉搜索树，输入为节点和节点序
void printBST(tNode* root,int start, int isLeft){
    if(isLeft == -1)
        printf("root node is %d\n", root->value);
    else
        printf("the %dth node is %d as %s\n",
            start,root->value,
            isLeft ? "left" : "right");
    //如果当前节有子节点，则继续打印这个子节点和节点序
    if (root->left!=NULL)
        printBST(root->left,start+1, 1);
    if (root->right!=NULL)
        printBST(root->right,start+1, 0);
}

最终在主函数中验证

tNode* initBST(){
    tNode* root;
    root->left=NULL;
    root->right=NULL;
    root->value=10;     //以上初始化根节点

    int init[10]={1,11,5,12,2,4,19,11,8,7};
    for (int i = 0; i < 10; i++)
        insertNode(root,init[i]);

    return root;
}

void testA(){
    tNode* root = initBST();    
    printBST(root,0,-1);
}

int main(){
    testA();
    return 0;
}

其结果为

> gcc .\cTrees.c
> .\a.exe
root node is 10
the 1th node is 1 as left   //第一代节点，10的左子节点
the 2th node is 5 as right  //第二代节点，1的右子节点
the 3th node is 2 as left   //第三代节点，5的左子节点
the 4th node is 4 as right  //第四代节点，2的右子节点
the 3th node is 8 as right  //第三代节点，5的右子节点
the 4th node is 7 as left   //第四代节点，8的左子节点
the 1th node is 11 as right //第一代节点，10的右子节点
the 2th node is 11 as left  //第二代节点，11的左子节点
the 2th node is 12 as right //第二代节点，11的右子节点
the 3th node is 19 as right //第三代节点，12的右子节点
>

生成的树为

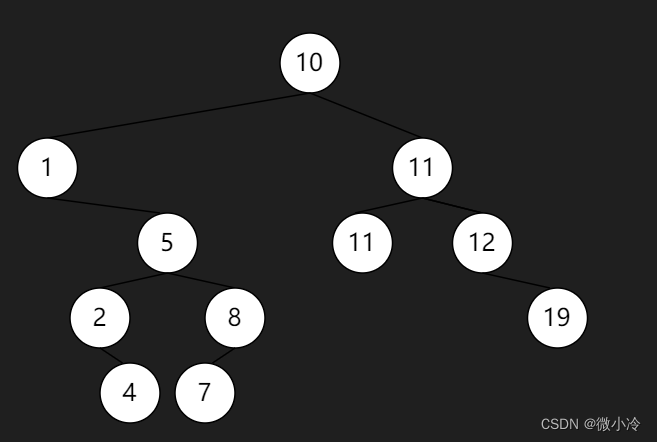
搜索节点

BST的结构特征，主要目的是便于搜索，接下来就为其添加新搜索功能。其中，搜索与插入如出一辙，而且更加简单，只需返回这个值的指针。同时，循环判定也变为while(root->value!=val)

//通过节点的值搜索节点地址，root为根节点
tNode* searchBST(tNode* root, int val){
    while (root->value!=val)
    {
        if (root->value<val && root->right!=NULL)
            root=root->right;
        else if (root->value>=val && root->left!=NULL)
            root=root->left;
        else
            return FALSE;
    }
    return root;
}

除了搜索到某个节点之外，有时还需要搜索BST的最大值或者最小值，其真正含义就是找到其最右端或者最左端的节点。

int findMin(tNode* root){
    if(root->left != NULL)
        return findMin(root->left);
    return root->value;
}

int findMax(tNode* root){
    if(root->right != NULL)
        return findMax(root->left);
    return root->value;
}

删除节点

删除节点相对复杂，毕竟涉及到其父子节点和兄弟节点之间的大小关系。

记将要被删除的节点为 $D$ ，其父节点为 $D_F$ 。若 $D$ 无子，那当然皆大欢喜，只需将 $D_F$ 指向 $D$ 的指针变成NULL；如果只有一个子节点 $D_L$ ，也并不麻烦，只需将 $D_F$ 指向 $D$ 的指针改为指向 $D_L$ 。

如果 $D$ 的左子节点为 $D_L$ ，右子节点为 $D_R$ ，那问题就比较麻烦了，需要找到左子节点中的最大值，或者右子节点中的最小值 $m$ ，然后把这个 $m$ 对应的节点删除。

//删除节点的值，root为根节点，delNode为待删除节点
void deleteNode(tNode* delNode){
    tNode* pNode;
    // 左右子节点均为NULL
    if(delNode->left==NULL&&delNode->right==NULL){
        pNode = delNode->father;        //当前节点的父节点
        if(delNode->value>pNode->value)
            pNode->right=NULL;
        else
            pNode->left=NULL;
    }
    // 左右子节点均不为NULL
    else if(delNode->left!=NULL&&delNode->right!=NULL){
        pNode = delNode->right;
        //替换为右子节点中的最小值
        delNode->value = findMin(pNode);  
        // 删除右子节点中的最小值
        while(pNode->left != NULL)
            pNode = pNode->left;
        pNode->father->left = NULL;
    }
    else{
        pNode = (delNode->left==NULL) \
            ? delNode->right : delNode->left;
        delNode->value = pNode->value;
        delNode->right = pNode->right;
        delNode->left = pNode->left;
    }
}

验证一下

void testB(){
    tNode* root = initBST();    
    tNode* sNode=searchBST(root,5);
    deleteNode(sNode);
    printBST(root,0);
}

int main(){
    testB();
    return 0;
}

结果为

PS E:\Code\AlgC> gcc .\cTrees.c
PS E:\Code\AlgC> .\a.exe       
root node is 10
the 1th node is 1 as left
the 2th node is 7 as right
the 3th node is 2 as left
the 4th node is 4 as right
the 3th node is 8 as right
the 1th node is 11 as right
the 2th node is 11 as left
the 2th node is 12 as right
the 3th node is 19 as right