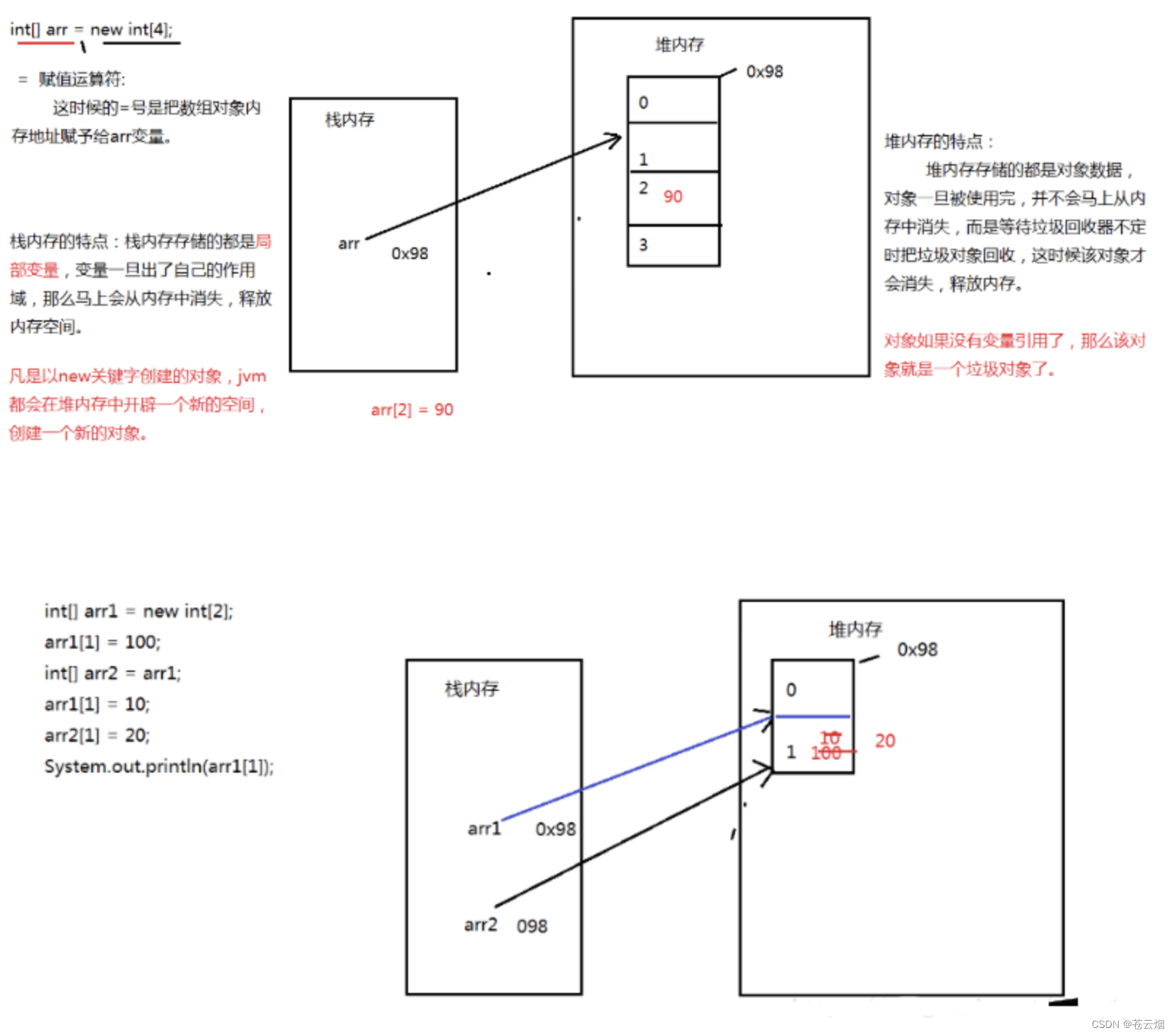
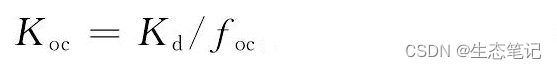三角形
- 三角形面积公式
S = 1 2 b c s i n A = 1 2 a c s i n B = 1 2 a b s i n C S=\frac{1}{2}bcsinA=\frac{1}{2}acsinB=\frac{1}{2}absinC S=21bcsinA=21acsinB=21absinC(正弦定理);
S = p ( p − a ) ( p − b ) ( p − c ) S=\sqrt{p(p-a)(p-b)(p-c)} S=p(p−a)(p−b)(p−c),其中a,b,c为三边长, p = 1 2 ( a + b + c ) p=\frac{1}{2}(a+b+c) p=21(a+b+c);
S = a + b + c 2 r S=\frac{a+b+c}{2}r S=2a+b+cr,其中a,b,c为三边长,r为内切圆半径;
S = a b c 4 R S=\frac{abc}{4R} S=4Rabc,其中a,b,c为三边长,R为外接圆半径;
边长为a的等边三角形的面积为 S = 3 4 a 2 S=\frac{\sqrt{3}}{4}a^2 S=43a2。
四边形
-
对角线相互垂直的四边形其面积等于对角线乘积的一半。
-
中点四边形的面积等于原四边形面积的一半。
-
同高模型:面积之比等于底边的边长之比。
-
一半模型:如图
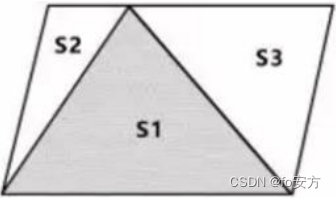
平行四边形被分成 3 个三角形,则ܵ S 1 = S 2 + S 3 = S_1=S_2+S_3= S1=S2+S3=平行四边形面积的一半。 -
蝴蝶定理
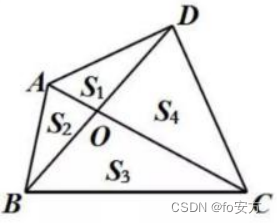
结论: S 1 ∗ S 3 = S 2 ∗ S 4 S_1*S_3=S_2*S_4 S1∗S3=S2∗S4
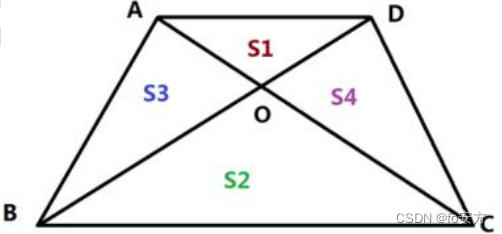
结论: S 1 ∗ S 2 = S 3 ∗ S 4 : S 3 = S 4 : S 1 S 2 = ( A D B C ) 2 S_1*S_2=S_3*S_4:S_3=S_4:\frac{S_1}{S_2}=(\frac{AD}{BC})^2 S1∗S2=S3∗S4:S3=S4:S2S1=(BCAD)2 -
过平行四边形中心的任一直线都把该平行四边形的面积分成相等的两部分。
-
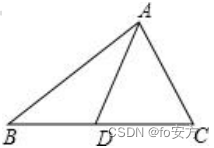
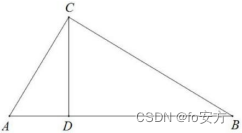
中线长定理:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍。如图,AD 为 BC 边上的中线,则 。
-
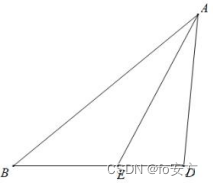
三角形任一内角平分线分其对边所成的两条线段与夹这个角的两边对应成比例。
如图,AE 平分∠BAD 交△ABD 的边 BD 于点 E,那么有 AB/AD=BE/DE.
-
直角三角形两直角边乘积等于斜边与斜边上高的乘积。
-
如图,在直角三角形 ABC 中,CD 是斜边 AB 上的高,则有: C D 2 = A D ∗ D B , A C 2 = A D ∗ A B , B C 2 = B D ∗ B A CD^2=AD*DB,AC^2=AD*AB,BC^2=BD*BA CD2=AD∗DB,AC2=AD∗AB,BC2=BD∗BA
圆形
若
x
2
+
y
2
=
r
2
(
r
>
0
)
x^2+y^2=r^2(r>0)
x2+y2=r2(r>0),则
−
r
a
2
+
b
2
≤
a
x
+
b
y
≤
r
a
2
+
b
2
-r\sqrt{a^2+b^2}≤ax+by≤r\sqrt{a^2+b^2}
−ra2+b2≤ax+by≤ra2+b2,即ax+by的最大值为
r
a
2
+
b
2
r\sqrt{a^2+b^2}
ra2+b2,最小值为
−
r
a
2
+
b
2
-r\sqrt{a^2+b^2}
−ra2+b2。
过圆
x
2
+
y
2
=
r
2
x^2+y^2=r^2
x2+y2=r2上一点
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0)的切线方程为
x
0
x
+
y
0
y
=
r
2
x_0x+y_0y=r^2
x0x+y0y=r2。
过圆
x
2
+
y
2
=
r
2
x^2+y^2=r^2
x2+y2=r2上一点
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0),作圆的两条切线方程,切点分别为A、B,则过A、B两点的直线方程为
x
0
x
+
y
0
y
=
r
2
x_0x+y_0y=r^2
x0x+y0y=r2。
若两个圆相交,则将两圆方程相减即得两圆相交公共弦所在的直线方程。
线
- 对称问题
设点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0)关于直线ax+by+c=0的对称点坐标为 ( x 1 , y 1 ) (x_1,y_1) (x1,y1),则
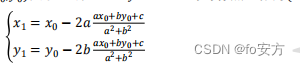
若对称轴的斜率为 1 或-1,求对称点的坐标可以把已知点的坐标分别代入对称轴方程,代入方法为“代横得纵,代纵得横”。 - 对于二元一次绝对值方程
∣
a
x
+
m
∣
+
∣
b
y
+
n
∣
=
c
|ax+m|+|by+n|=c
∣ax+m∣+∣by+n∣=c,若 a≠b,方程表示的图形为菱形;若a=b,方程表示的图形为正方形。
方程 ∣ a x + m ∣ + ∣ b y + n ∣ = c |ax+m|+|by+n|=c ∣ax+m∣+∣by+n∣=c所表示图形的面积为直线与两坐标轴所围成三角形面积的4 倍。 - 直线 a 1 x + b 1 y + c 1 = 0 a_1x+b_1y+c_1=0 a1x+b1y+c1=0与直线 a 2 x + b 2 y + c 2 = 0 a_2x+b_2y+c_2=0 a2x+b2y+c2=0垂直 ⟺ a 1 a 2 + b 1 b 2 = 0 a_1a_2+b_1b_2=0 a1a2+b1b2=0。