四、当i>A.heap-size/2 时，调用 MAX-HEAPIFY(A，i)会有什么结果?

文心一言：

当 i > A.heap-size/2 时，调用 MAX-HEAPIFY(A, i) 会将 A[i] 与其子树中的最大元素进行交换，并将 A[i] 视为新的根节点。这个操作会使得以 A[i] 为根节点的子树满足最大堆的性质，即根节点比其左右孩子大。

具体来说，假设 A[i] 的左孩子为 A[2i]，右孩子为 A[2i+1]，则 MAX-HEAPIFY(A, i) 的操作过程如下：

1.将 A[i] 与其子树中的最大元素进行交换，即与 A[2i] 或 A[2i+1] 进行交换。

2.递归调用 MAX-HEAPIFY(A, 2i) 对左子树进行操作，将左子树的最大元素交换到 A[2i]。

3.递归调用 MAX-HEAPIFY(A, 2i+1) 对右子树进行操作，将右子树的最大元素交换到 A[2i+1]。

通过这些操作，以 A[i] 为根节点的子树会满足最大堆的性质，即 A[i] 大于其左右孩子。同时，由于 i > A.heap-size/2，所以以 A[i] 为根节点的子树是整个堆的左半部分或右半部分，而另一半子树则满足最大堆的性质。因此，整个堆仍然满足最大堆的性质。

在这里插入图片描述

讯飞星火：

当 i > A.heap-size/2 时，调用 MAX-HEAPIFY(A,i) 会将 A[i] 与 A[A.heap-size/2] 进行比较，并将较小的值与 A[A.heap-size/2] 交换。然后，MAX-HEAPIFY(A,A.heap-size/2) 将被递归地调用，直到 i <= A.heap-size/2。这个过程会重新组织堆结构，使得 A[A.heap-size/2] 成为新的根节点。这样可以保持堆的性质，即每个子节点的值都小于或等于其父节点的值。

在这里插入图片描述

华为盘古：

在这里插入图片描述

360智脑：

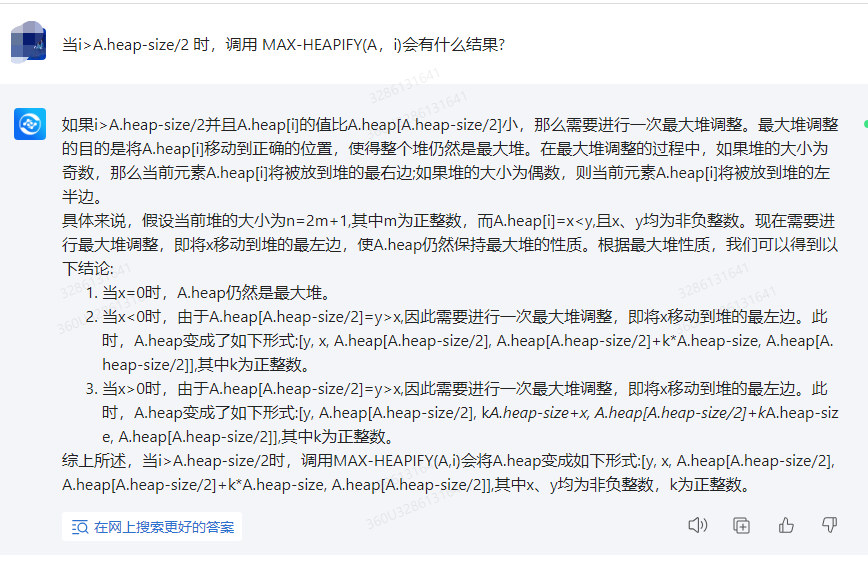
如果i>A.heap-size/2并且A.heap[i]的值比A.heap[A.heap-size/2]小，那么需要进行一次最大堆调整。最大堆调整的目的是将A.heap[i]移动到正确的位置，使得整个堆仍然是最大堆。在最大堆调整的过程中，如果堆的大小为奇数，那么当前元素A.heap[i]将被放到堆的最右边;如果堆的大小为偶数，则当前元素A.heap[i]将被放到堆的左半边。

具体来说，假设当前堆的大小为n=2m+1,其中m为正整数，而A.heap[i]=x<y,且x、y均为非负整数。现在需要进行最大堆调整，即将x移动到堆的最左边，使A.heap仍然保持最大堆的性质。根据最大堆性质，我们可以得到以下结论:

1.当x=0时，A.heap仍然是最大堆。

2.当x<0时，由于A.heap[A.heap-size/2]=y>x,因此需要进行一次最大堆调整，即将x移动到堆的最左边。此时，A.heap变成了如下形式:[y, x, A.heap[A.heap-size/2], A.heap[A.heap-size/2]+k*A.heap-size, A.heap[A.heap-size/2]],其中k为正整数。

3.当x>0时，由于A.heap[A.heap-size/2]=y>x,因此需要进行一次最大堆调整，即将x移动到堆的最左边。此时，A.heap变成了如下形式:[y, A.heap[A.heap-size/2], kA.heap-size+x, A.heap[A.heap-size/2]+kA.heap-size, A.heap[A.heap-size/2]],其中k为正整数。

综上所述，当i>A.heap-size/2时，调用MAX-HEAPIFY(A,i)会将A.heap变成如下形式:[y, x, A.heap[A.heap-size/2], A.heap[A.heap-size/2]+k*A.heap-size, A.heap[A.heap-size/2]],其中x、y均为非负整数，k为正整数。

在这里插入图片描述

chatglm：

当 i>A.heap-size/2 时，调用 MAX-HEAPIFY(A,i) 会将堆中的最大值交换到数组下标为 i 的位置。

具体来说，MAX-HEAPIFY(A,i) 函数的作用是将堆中下标为 i 的节点 (假设当前堆采用完全二叉树表示) 与其两个子节点中的最大值进行交换。如果 i 是堆的最高位 (即 i=A.heap-size-1)，则只需要与 i 的左子节点进行交换；否则，需要与 i 的左子节点和右子节点中的最大值进行交换。交换后，i 的位置上仍然是堆中的最大值。

如果 i>A.heap-size/2，则说明 i 是堆的中间位置，此时需要将其与 i 的子节点中的最大值进行交换，以维护堆的性质。交换后，i 的位置上仍然是堆中的最大值，但是交换后的节点可能会影响到堆的平衡性质，因此可能需要继续调整堆的其他节点，以使堆保持平衡。

在这里插入图片描述

chatgpt：

当 i > A.heap-size/2 时，MAX-HEAPIFY(A, i) 函数调用将没有任何结果。这是因为在堆的二叉树表示中，对于任意的结点 i，其左子结点下标为 2i，右子结点下标为 2i+1。由于堆是完全二叉树，它的所有叶子结点都位于下标大于 A.heap-size/2 的位置上。因此，i > A.heap-size/2 意味着结点 i 是一个叶子结点，它没有子结点，所以不需要进行堆调整（即调用 MAX-HEAPIFY）。

在这里插入图片描述