题目

例如 y = x^ 5 +e^x+3x−3，求解y = 0的解

问题分析

首先要构造y = 0的损失函数，让这个损失函数是凸的，也就是可以有最优解，并且是可到的，比较容易想到的是mse平方误差，我们要让y和0之间绝对误差最小。loss=(y-0)^2

解题方法

求导数

我们有了损失函数，就可以用梯度下降法，求解loss的最优解x。
梯度计算可以有两种方法，一种是链式求导法求梯度：
gradient(loss, x) = 2*(x^ 5 +e^x+3x−3) * (5 * x ^ 4 + e^x + 3)
另一种方法是近似求导：
gradient(loss, x) = (loss(x+delta)-loss(x-delta))/(2*delta)
两种方法都是可以的。

求x近似解

一般是迭代一定的步数，或者loss小于某个值，就认为是已经找到最优解了。

伪代码：
alpha = 0.01 # 步长
delta = 0.000001 #损失函数停止条件
loss = (y - 0) ^ 2
while loss > delta:
	x = x - gradient(loss, x) 
	loss = loss(y(x) )
print('loss: %f, y: %f, x: %f' %(loss, y, x)

代码实现

# 可以求y=任意值的最优解x
class Opm:
    def __init__(self):
        self.e1 = 2.712
        self.delta = 0.0001

    def loss(self, x, y_real):
        y = (x**5 + self.e1 ** x +3*x - 3)
        loss = (y-y_real)**2
        return loss, y

    def gradient(self, x, y_real):
        grad = 2*(x**5 + self.e1**x + 3*x-3-y_real)*(5*(x**4) + self.e1**x +3)
        return grad

    def gradient1(self, x, y_real):
        grad = (self.loss(x+self.delta, y_real)[0]-self.loss(x-self.delta, y_real)[0])/(2*self.delta)
        return grad

    def sgd(self, x, y):
        # x = 0 #起始点，深度模型中相当于初始化的变量
        # y = 1 #要求解的最优质，相当于label
        alpha = 0.01 #步长
        stop_value = 0.0001 #提前终止的阈值
        step = 0
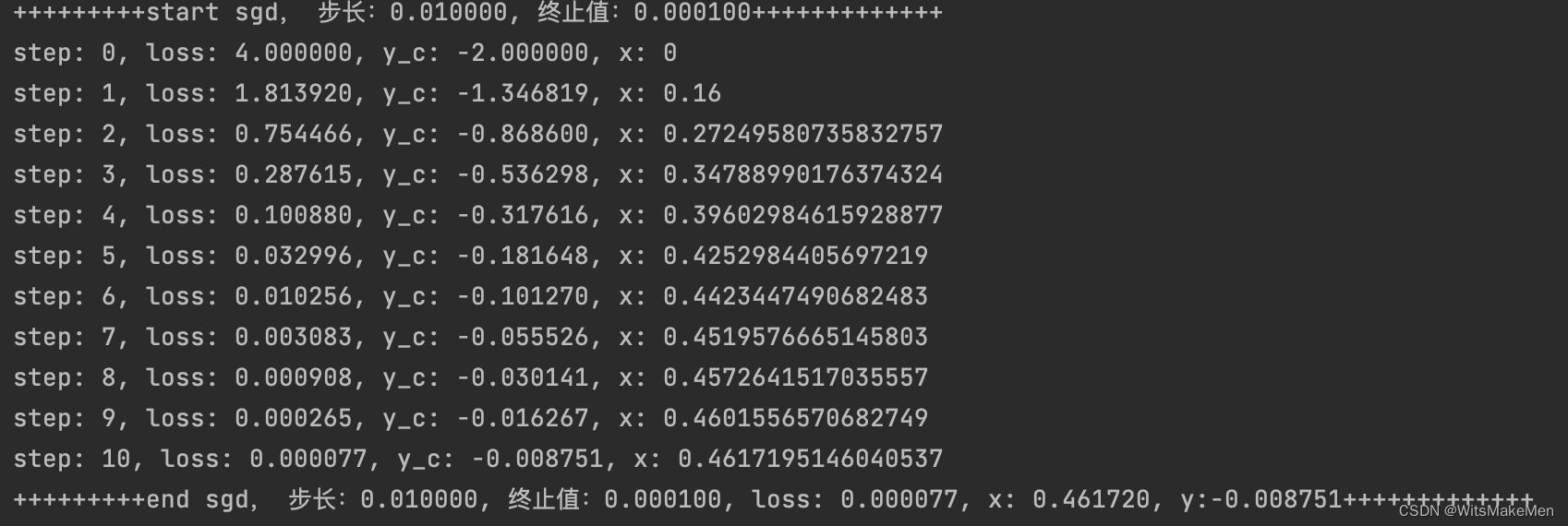
        print('+++++++++start sgd， 步长：%f, 终止值：%f+++++++++++++' % (alpha, stop_value))
        while True:
            loss, y_c = self.loss(x, y)
            print('step: %d, loss: %f, y_c: %f, x: %s' % (step, loss, y_c, x))
            if loss<stop_value:
                break
            # x = x - self.gradient1(x, y) * alpha
            x = x - self.gradient(x, y) * alpha
            step += 1
        print('+++++++++end sgd， 步长：%f, 终止值：%f, loss: %f, x: %f, y:%f+++++++++++++' % (alpha, stop_value, loss, x, y_c))
        return loss, x, y_c
opm = Opm()
opm.sgd(0, 0)