LeetCode 75 —— 62. 不同路径

news2024/12/22 20:50:40

LeetCode 75 —— 62. 不同路径

一、题目描述：

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7

输出：28

示例 2：

输入：m = 3, n = 2

输出：3

解释：

从左上角开始，总共有 3 条路径可以到达右下角。

向右 -> 向下 -> 向下
向下 -> 向下 -> 向右
向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3

输出：28

示例 4：

输入：m = 3, n = 3

输出：6

提示：

1 <= m, n <= 100

题目数据保证答案小于等于 2 * 10^9

来源：力扣（LeetCode）

链接：https://leetcode.cn/problems/unique-paths

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

二、思路分析：

这道题考察了什么思想？你的思路是什么？

面对这道题目我的第一想法是能不能找寻规律，利用排列组合的方法解题，虽然我没有找到哈~但是我看题解有找到规律的：

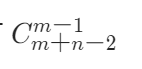
这个规律其实不太好找，不过我们根据第一个m=3，n=2的例子，可以发现，我们到这里可以有向下一步，向右两步，就一定能到达终点。

然后我又想了动态规划的方法，这道题应该是一道典型的动态规划题目，我们将起点到每一个点的路径设置为到其左边那个点的路径条数加上到其上面那个点的路径条数之和。所以有动态规划转移方程：
```
f(x,y) = f(x-1)(y) + f(x)(y-1)
```
不过需要注意的是，我们要将f(x,0)和f(0,y)的值设置为1。很好就可以理解，确实到他们的路径只有一条！
做题的时候是不是一次通过的，遇到了什么问题，需要注意什么细节？

不是一次通过的，注意什么时候用m，什么时候用n。我刚开始在此处有些失误！

有几种解法，哪种解法时间复杂度最低，哪种解法空间复杂度最低，最优解法是什么？其他人的题解是什么，谁的效率更好一些？用不同语言实现的话，哪个语言速度最快？

动态规划优化：因为我们每次只记录需要 dp[i-1][j],dp[i][j-1]

class Solution {
    public int uniquePaths(int m, int n) {
        int[] pre = new int[n];
        int[] cur = new int[n];
        Arrays.fill(pre, 1);
        Arrays.fill(cur,1);
        for (int i = 1; i < m;i++){
            for (int j = 1; j < n; j++){
                cur[j] = cur[j-1] + pre[j];
            }
            pre = cur.clone();
        }
        return pre[n-1]; 
    }
}

作者：powcai
链接：https://leetcode.cn/problems/unique-paths/solution/dong-tai-gui-hua-by-powcai-2/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

class Solution {
    public int uniquePaths(int m, int n) {
        int[] cur = new int[n];
        Arrays.fill(cur,1);
        for (int i = 1; i < m;i++){
            for (int j = 1; j < n; j++){
                cur[j] += cur[j-1] ;
            }
        }
        return cur[n-1];
    }
}

作者：powcai
链接：https://leetcode.cn/problems/unique-paths/solution/dong-tai-gui-hua-by-powcai-2/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

三、AC 代码：

func uniquePaths(m int, n int) int {
    dp := make([][]int,m)
    for i := range dp{
        dp[i] = make([]int,n)
        dp[i][0] = 1
    }
    for i:=0;i<n;i++{
        dp[0][i] = 1
    }

    for i:=1;i<m;i++{
        for j:=1;j<n;j++{
            dp[i][j] = dp[i-1][j] + dp[i][j-1]
        }
    }
    return dp[m-1][n-1]
}