300. 最长递增子序列

首先明确什么是子序列

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序

不一定要连续 可以删除部分元素 但是要保证相对顺序

1. dp[i]的定义

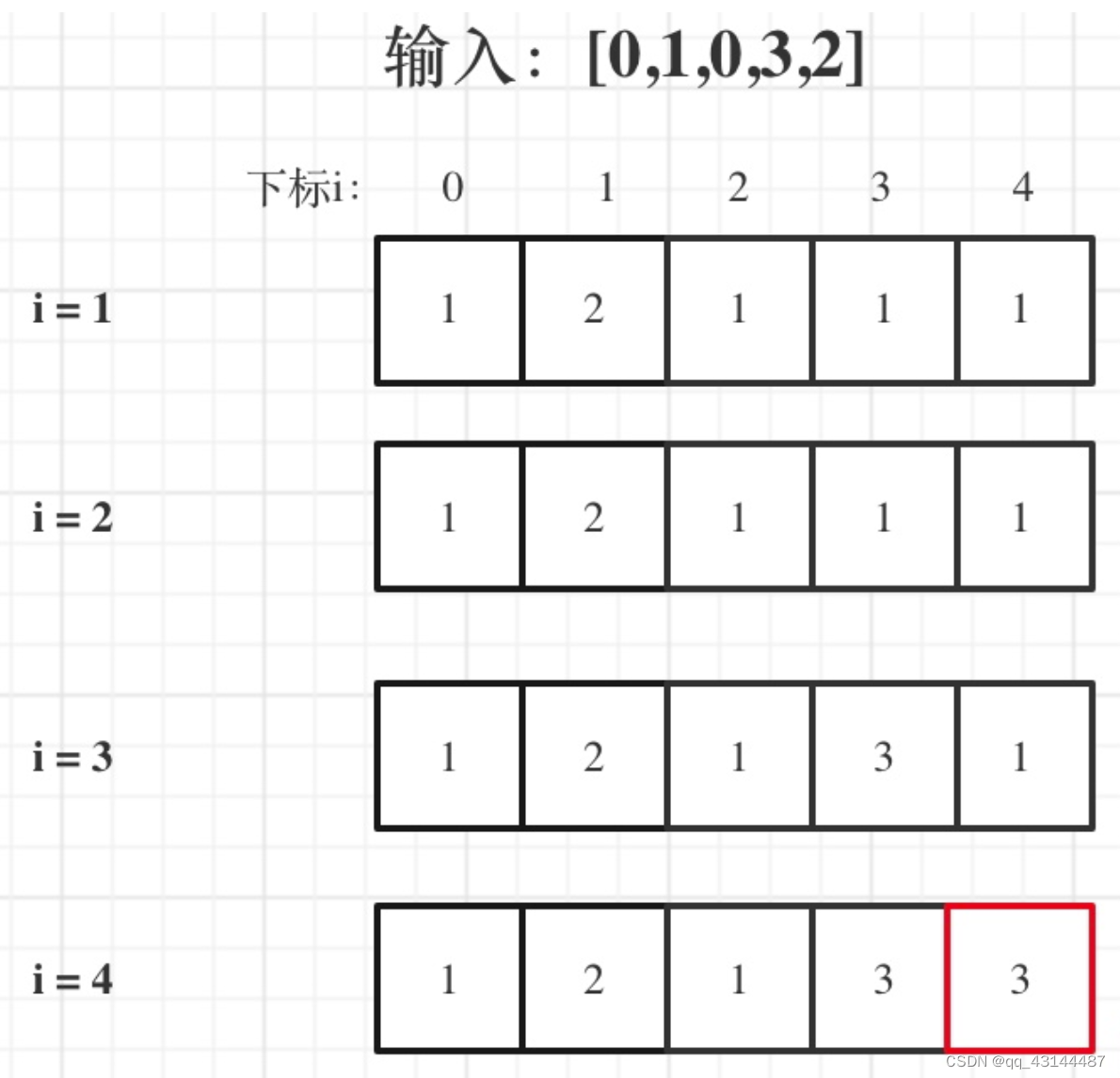
        dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度

2. 状态转移方程

if(nums[i] > nums[j]){
   dp[i] = Math.max(dp[i], dp[j] + 1);
}

 注意这里不是要dp[i] 与 dp[j] + 1进行比较，而是我们要取dp[j] + 1的最大值

3. dp[i]的初始化

        每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1.

4. 确定遍历顺序

        从前向后遍历

5. 举例推导dp数组

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);

        for(int i = 1; i < nums.length; i++){
            for(int j = 0; j < i; j++){
                if(nums[i] > nums[j]){
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
        }
        int res = Integer.MIN_VALUE;
        for(int num : dp){
            res = Math.max(res, num);
        }
        return res;
    }
}

 

674. 最长连续递增序列

这题难度一下子就小了

本题要求的是最长连续递增序列  === 子数组

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);

        for(int i = 1; i < nums.length; i++){
            if(nums[i] > nums[i-1]){
                dp[i] = dp[i-1] + 1;
            }
        }

        int res = Integer.MIN_VALUE;
        for(int num : dp){
            res = Math.max(res, num);
        }

        return res;
    }
}

本题也可以用贪心来做

public static int findLengthOfLCIS(int[] nums) {
    if (nums.length == 0) return 0;
    int res = 1; // 连续子序列最少也是1
    int count = 1;
    for (int i = 0; i < nums.length - 1; i++) {
        if (nums[i + 1] > nums[i]) { // 连续记录
            count++;
        } else { // 不连续，count从头开始
            count = 1;
        }
        if (count > res) res = count;
    }
    return res;
}

718. 最长重复子数组

题目中说的子数组，其实就是连续子序列。

1. 确定dp数组（dp table）以及下标的含义

         dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]

2. 确定递推公式

 if(nums1[i-1] == nums2[j - 1]){
       dp[i][j] = dp[i-1][j-1] + 1;
}

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);

        for(int i = 1; i < nums.length; i++){
            if(nums[i] > nums[i-1]){
                dp[i] = dp[i-1] + 1;
            }
        }

        int res = Integer.MIN_VALUE;
        for(int num : dp){
            res = Math.max(res, num);
        }

        return res;
    }
}