1、题目
用 1 × 2 1 \times 2 1×2 的瓷砖,把 N × 2 N \times 2 N×2 的区域填满,返回铺瓷砖的方法数。
2、思路
记录 F(n) 表示空的
n
∗
2
n * 2
n∗2 区域的铺瓷砖方法数。
如果第一块瓷砖 A 竖着放,则问题就变成了
F
(
n
−
1
)
F(n-1)
F(n−1) 即空的
(
n
−
1
)
∗
2
(n-1) * 2
(n−1)∗2 区域铺瓷砖的方法数:
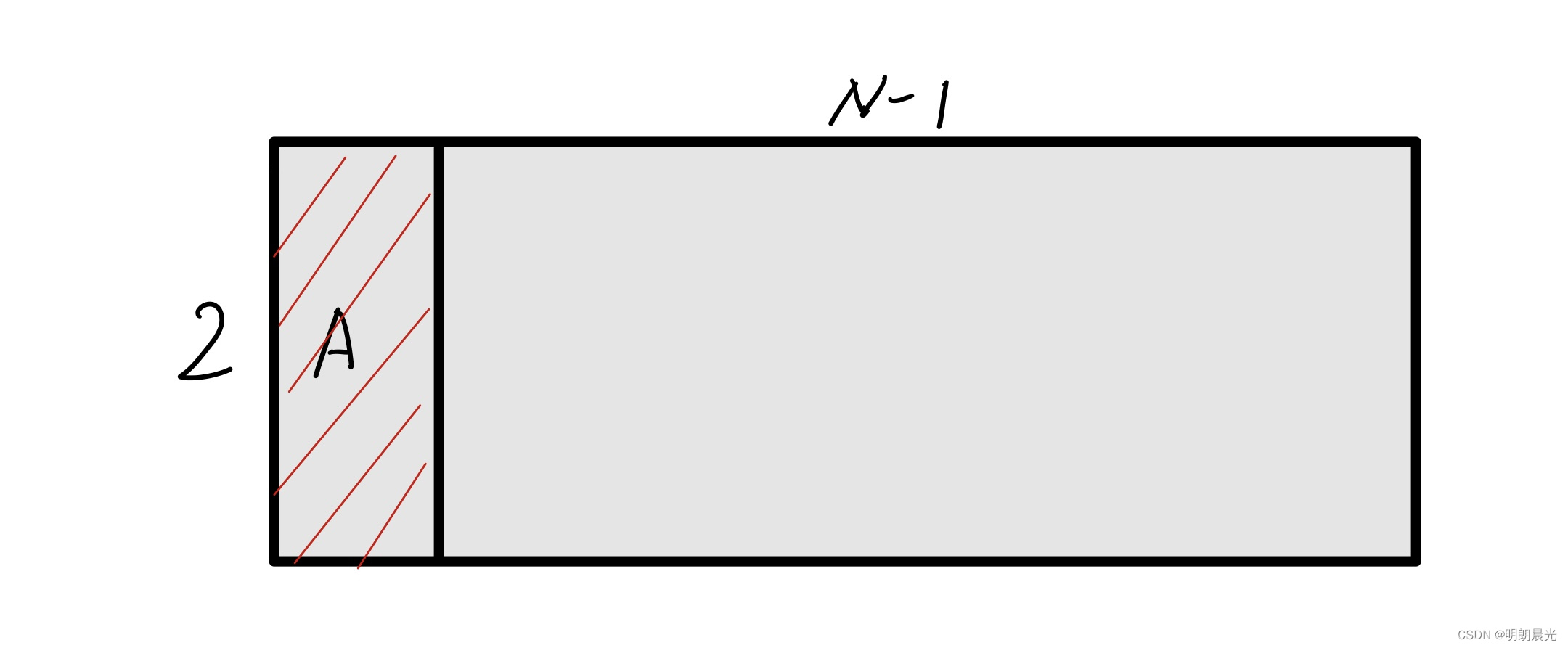
如果第一块砖 A 横着放,那它下面必须横着放另一块,问题就变成F(n-2) 即空的
(
n
−
2
)
∗
2
(n-2) * 2
(n−2)∗2 区域铺瓷砖的方法数:
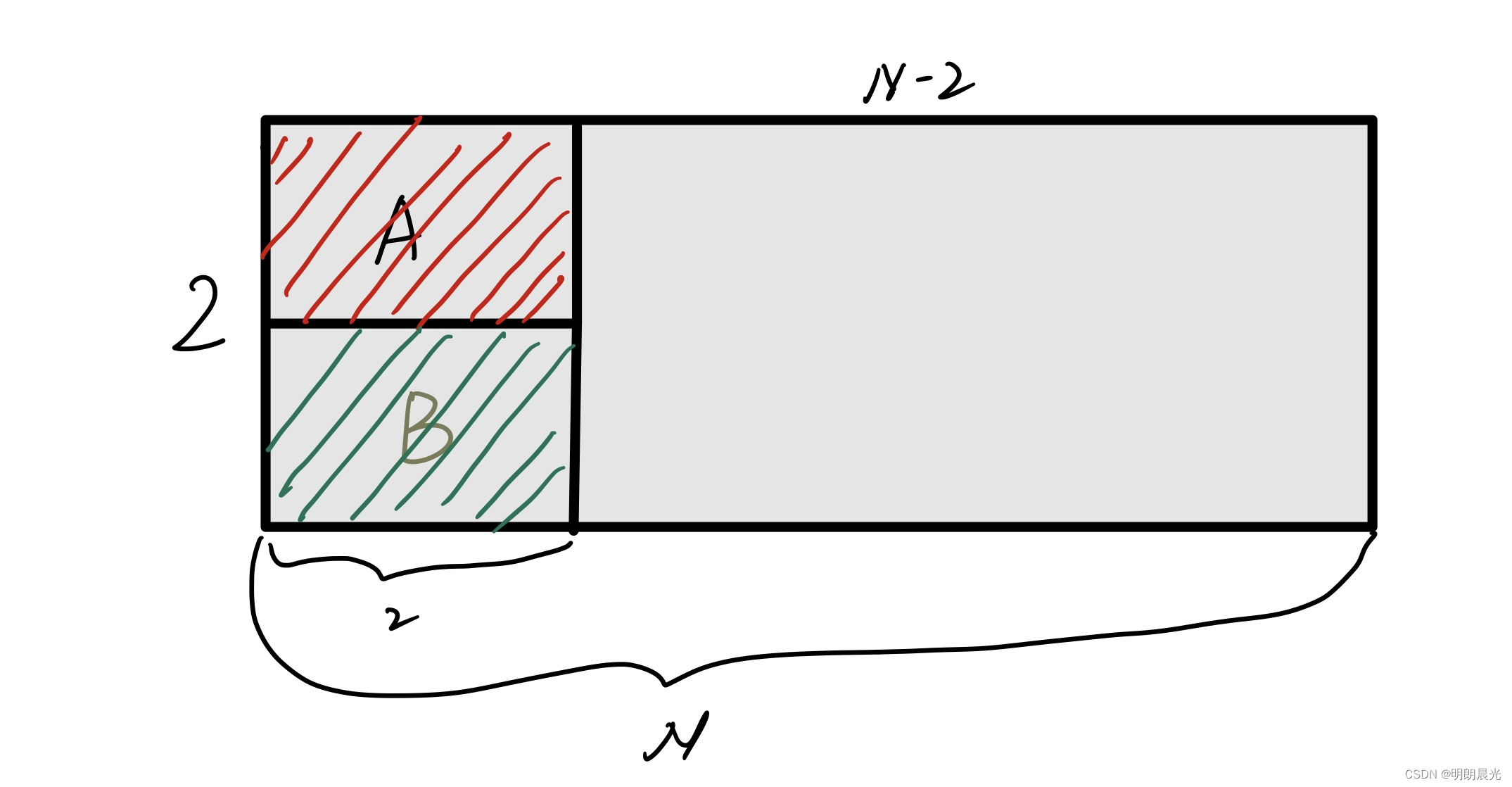
所以:
F
(
n
)
=
F
(
n
−
1
)
+
F
(
n
−
2
)
F(n) = F(n-1) + F(n-2)
F(n)=F(n−1)+F(n−2),依然是个斐波那契数列问题。
初始项:F(1) = 1,F(2) = 2,2阶矩阵问题。
代码实现同达标的字符串