1 链表

链表是线性数据结构（数据元素之间存在着“一对一”关系），链表中的每个元素是一个包含数据data和引用字段的对象，引用字段只有next为单向链表，同时又prev和next为双向链表。

1.1 链表基本操作

链表读取第 i 个节点或查找指定值的节点，均需要从头遍历，时间复杂度为O(n)。

在不考虑查找节点的过程的情况下，更新（替换data），插入（新节点next指针指向插入位置节点，前一节点的next指针指向新节点）、删除（前一节点next指针指向下一节点，当前节点置空），时间复杂度均为O(1)。

1.2 设计链表

设计单向链表的实现。单链表中的节点应该具有两个属性：val 和 next。val 是当前节点的值，next 是指向下一个节点的指针/引用。假设链表中的所有节点都是 0 ~ size - 1 的。

class LinkNode<T> {
  val: T;
  next: LinkNode<T> | null;

  constructor(val: T, next?: LinkNode<T> | null) {
    this.val = val;
    this.next = next ?? null;
  }
}

class MyLinkedList<T> {
  size: number; // 链表长度
  head: LinkNode<T> | null; // 头结点
  constructor() {
    this.size = 0;
    this.head = null;
  }
  /**
   * 获取链表中 index 位置的节点。如果索引无效，则返回 null。
   * @param index
   */
  getNode(index: number): LinkNode<T> | null {
    if (index < 0 || index >= this.size) {
      return null;
    }
    // index 有效，所以 node.next 和 node.val 是存在的。
    let node = this.head as LinkNode<T>;
    for (let i = 0; i < index; i++) {
      node = node.next as LinkNode<T>;
    }
    return node;
  }
  /**
   * 获取链表中 index 位置的节点值。如果索引无效，则返回-1。
   * @param index
   */
  get(index: number): T | -1 {
    const node = this.getNode(index);
    return node?.val ?? -1;
  }
  /**
   * 在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
   * @param val
   */
  addAtHead(val: T): void {
    const newHead = new LinkNode(val);
    newHead.next = this.head;
    this.head = newHead;
    this.size = this.size + 1;
  }
  /**
   * 将值为 val 的节点追加到链表的最后一个元素。
   * @param val
   */
  addAtTail(val: T): void {
    const oldTailNode = this.getNode(this.size - 1);
    const newTailNode = new LinkNode(val);
    this.size = this.size + 1;
    if (oldTailNode === null) {
      this.head = new LinkNode(val);
      return;
    }
    oldTailNode.next = newTailNode;
  }
  /**
   * 在链表中的 index 位置之前添加值为 val  的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。如果 index 小于0，则在头部插入节点。
   * @param index
   * @param val
   */
  addAtIndex(index: number, val: T): void {
    if (index > this.size) return;
    // 尾插
    if (index === this.size) {
      this.addAtTail(val);
      return;
    }
    // 头插
    if (index < 0) {
      this.addAtHead(val);
      return;
    }
    const prevNode = this.getNode(index - 1) as LinkNode<T>;
    const node = new LinkNode(val);
    node.next = prevNode.next;
    prevNode.next = node;
    this.size = this.size + 1;
  }

  /**
   * 如果索引 index 有效，则删除链表中的第 index 个节点。
   * @param index
   */
  deleteAtIndex(index: number): void {
    // index 无效
    if (index < 0 || index >= this.size || this.size === 0) return;
    this.size = this.size - 1;
    // 删除头节点
    if (index === 0) {
      this.head = this.head?.next as LinkNode<T> | null;
      return;
    }
    const prevNode = this.getNode(index - 1) as LinkNode<T>;
    const deleteNode = prevNode.next as LinkNode<T>;
    prevNode.next = deleteNode.next;
  }
}

1.3 剑指 offer 链表算法题（typescript 版）

从尾到头打印链表

链表倒数第k个节点

反转链表

合并两个排序链表

复杂链表的复制

删除链表中的重复节点

两个链表的第一个公共节点

链表中环的入口节点

2 树

2.1 基本概念

树是非线性逻辑结构，是n（n≥0）个节点的有限集。当n=0时，称为空树。树的每个节点有一个节点值和包含所有子节点的列表，从图的角度看，即N个节点的N - 1条边的有向无环图。树的最大层级数，被称为树的高度或深度。树中最多子节点数称为树的度。

而最常用且典型的是二叉树，即每个节点最多只有两个子节点。两个孩子节点的顺序是固定的（与二度树不同）。

满二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上。

完全二叉树是具有与同深度的按层级顺序1 到 n 编号的满二叉树完全对应的节点编号的二叉树。

二叉树是逻辑结构，物理结构可以是链式存储结构，或者是数组。

链式存储结构：存储数据的data变量、指向左孩子的left指针、指向右孩子的right指针。

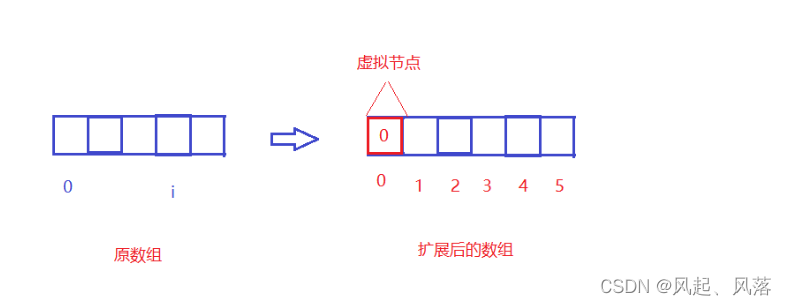
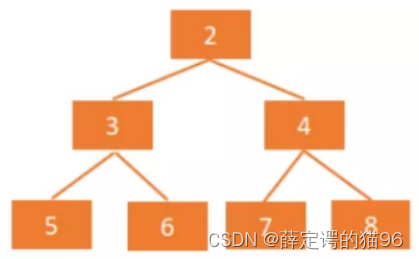
数组：按层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空出来：

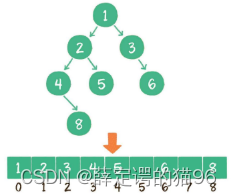
如上图，当前节点的下标是parent，那么它的左孩子节点下标就是2 × parent + 1；右孩子节点下标就是2 × parent + 2。反过来，假设一个左孩子节点的下标是lChild，那么它的父节点下标就是（lChild - 1）/ 2，同理，假设一个右孩子节点的下标是rChild，那么它的父节点下标就是（rChild - 2）/ 2，因此任何一个节点下标为child，其父节点下标为 Math.floor((child - 1) / 2)。数组存储更适合完全二叉树和满二叉树，对于稀疏二叉树，无疑是浪费空间的。

二叉树的应用主要是查找和维持相对顺序，比如二叉查找树（二叉搜索树）（左孩子 < 父节点 < 右孩子）和二叉堆（大根堆：左孩子 < 父节点 > 右孩子，小根堆：左孩子 > 父节点 < 右孩子）。对于一个节点分布相对均衡的二叉查找树来说，如果节点总数是n，那么搜索节点的时间复杂度就是O(logn)，和树的深度是一样的。而如果考虑插入有序的序列，树的高度和搜索时间都会退化成O(n)，就需要采用二叉树的自平衡，其应用有：红黑树、AVL树（二叉平衡树）等 。

2.2 二叉树的实现与遍历

二叉树遍历包括前序遍历，中序遍历，后序遍历，层序遍历。实现方法为递归遍历和迭代遍历。

二叉树的实现和递归遍历：

class BinaryTreeNode {
  key: string | number; // 节点的键
  parent: BinaryTreeNode | null; // 节点的父节点
  value: any; // 节点的值
  left: BinaryTreeNode | null; // 指向节点左孩子的指针
  right: BinaryTreeNode | null; // 指向节点右孩子的指针
  constructor(key: string | number, value = key, parent = null) {
    this.key = key;
    this.value = value;
    this.parent = parent;
    this.left = null;
    this.right = null;
  }
  get isLeaf() {
    return this.left === null && this.right === null;
  }
  get hasChildren() {
    return !this.isLeaf;
  }
}

class BinaryTree {
  // 根节点
  root: BinaryTreeNode;
  constructor(key: string, value = key) {
    this.root = new BinaryTreeNode(key, value);
  }

  /**
   * 中序遍历 （首先遍历左子树，然后访问根节点，最后遍历右子树）
   * @param node
   */
  *inOrderTraversal(node = this.root) {
    if (node) {
      const { left, right } = node;
      if (left) yield* this.inOrderTraversal(left);
      yield node;
      if (right) yield* this.inOrderTraversal(right);
    }
  }
  /**
   * 后序遍历 （首先遍历左子树，然后遍历右子树，最后访问根节点）
   * @param node
   */
  *postOrderTraversal(node = this.root) {
    if (node) {
      const { left, right } = node;
      if (left) yield* this.postOrderTraversal(left);
      if (right) yield* this.postOrderTraversal(right);
      yield node;
    }
  }
  /**
   * 前序遍历 （首先访问根节点，然后遍历左子树，最后遍历右子树）
   * @param node
   */
  *preOrderTraversal(node = this.root) {
    if (node) {
      const { left, right } = node;
      yield node;
      if (left) yield* this.preOrderTraversal(left);
      if (right) yield* this.preOrderTraversal(right);
    }
  }
  /**
   * 插入一个节点作为给定父节点的子节点
   * @param parentNodeKey
   * @param key
   * @param value
   * @param param3
   * @returns
   */
  insert(parentNodeKey: any, key: string, value = key, { left, right } = { left: true, right: true }) {
    for (const node of this.preOrderTraversal()) {
      if (node.key === parentNodeKey) {
        // 插入到某父节点下，如果不指定则插入到左右孩子中的空的那个
        const canInsertLeft = left && node.left === null;
        const canInsertRight = right && node.right === null;
        if (!canInsertLeft && !canInsertRight) return false; // 该父节点孩子节点不空余
        if (canInsertLeft) {
          node.left = new BinaryTreeNode(key, value, node);
          return true;
        }
        if (canInsertRight) {
          node.right = new BinaryTreeNode(key, value, node);
          return true;
        }
      }
    }
    return false;
  }
  /**
   * 从二叉树中删除一个节点及其子节点
   * @param key
   * @returns
   */
  remove(key: string) {
    for (const node of this.preOrderTraversal()) {
      if (node.left.key === key) {
        node.left = null;
        return true;
      }
      if (node.right.key === key) {
        node.right = null;
        return true;
      }
    }
    return false;
  }
  /**
   * 检索给定节点
   * @param key
   * @returns
   */
  find(key: string) {
    for (const node of this.preOrderTraversal()) {
      if (node.key === key) return node;
    }
    return undefined;
  }
}

前序遍历（迭代）：

/**
 * 前序遍历 （首先访问根节点，然后遍历左子树，最后遍历右子树）
 */
function preOrderTraversal(root: BinaryTreeNode | null) {
  if (root === null) return [];
  const result: number[] = [];
  const stack = [root];
  while (stack.length !== 0) {
    const current = stack.pop()!;
    result.push(current.value);
    const lChild = current.left;
    const rChild = current.right;
    // 栈后进先出，因此先右孩子入栈，然后左孩子入栈
    if (rChild !== null) stack.push(rChild);
    if (lChild !== null) stack.push(lChild);
  }
  return result;
}

中序遍历（迭代）：

/**
 * 中序遍历 （首先遍历左子树，然后访问根节点，最后遍历右子树）
 */
function inOrderTraversal(root: BinaryTreeNode | null) {
  if (root === null) return [];
  const result: number[] = [];
  const stack: BinaryTreeNode[] = [];
  let current: BinaryTreeNode | null = root;
  while (stack.length !== 0 || current !== null) {
    while (current !== null) {
      // 一直遍历到最左孩子节点
      stack.push(current);
      current = current.left;
    }
    if (stack.length !== 0) {
      // 栈非空
      const node = stack.pop()!;
      result.push(node.value);
      current = node.right; // 当前 -> 右
    }
  }
  return result;
}

后序遍历（迭代）：

/**
 * 后序遍历 （首先遍历左子树，然后遍历右子树，最后访问根节点）
 * @param node
 */
function postOrderTraversal(root: BinaryTreeNode | null) {
  if (root === null) return [];
  const result: number[] = [];
  // 转变成遍历 根节点 -> 右节点 -> 左节点
  // 遍历结果数组进行reverse, 即得到左节点 -> 右节点 -> 根节点
  let stack = [root];
  while (stack.length !== 0) {
    let current = stack.pop()!;
    result.push(current.value);
    let lChild = current.left;
    let rChild = current.right;
    // 交换和前序的顺序
    if (lChild !== null) stack.push(lChild);
    if (rChild !== null) stack.push(rChild);
  }
  return result.reverse(); // 反转即可
}

层序遍历：

/**
 * 层序遍历 （逐层遍历树结构，借助队列实现）
 * @param node
 */
function leverOrderTraversal(root: BinaryTreeNode | null) {
  if (root === null) return [];
  const result: number[] = [];
  const queue = [root]; // 队列（先入先出）
  while (queue.length !== 0) {
    // 队列非空
    const current = queue.shift()!; // 队首出队
    result.push(current.value);
    const leftChild = current.left;
    const rightChild = current.right;
    if (leftChild !== null) queue.push(leftChild);
    if (rightChild !== null) queue.push(rightChild);
  }
  return result;
}

2.3 剑指offer树算法题（typescript 版）

二叉树的深度

重建二叉树

从上到下打印二叉树

镜像二叉树

平衡二叉树

二叉树中和为某一值的路径

对称二叉树

二叉搜索树的后序遍历

二叉搜索树的第k个节点

树的子结构

二叉树的下一个节点

序列化二叉树

二叉搜索树与双向链表

3 图

3.1 图的基本操作

图是一种非线性逻辑结构，由一组节点或顶点以及一组表示这些节点之间连接的边组成。图可以是有向的或无向的，而它们的边可以分配数字权重。

3.2 图的设计与实现

interface Edge {
  a: GraphNode; // 边的起始节点
  b: GraphNode; // 边的目标节点
  weight?: number; // 边的可选数字权重值
}

interface GraphNode {
  key: string; // 节点的键
  value: any; // 节点的值
}

class Graph {
  directed: boolean;
  nodes: GraphNode[];
  edges: Map<string, Edge>;
  constructor(directed = true) {
    this.directed = directed;
    this.nodes = [];
    this.edges = new Map();
  }
  /**
   * 插入具有特定键和值的新节点
   * @param key
   * @param value
   */
  addNode(key: string, value = key) {
    this.nodes.push({ key, value });
  }
  /**
   * 在两个给定节点之间插入一条新边，可选择设置其权重
   * @param a
   * @param b
   * @param weight
   */
  addEdge(a: GraphNode, b: GraphNode, weight?: number) {
    this.edges.set(JSON.stringify([a, b]), { a, b, weight });
    if (!this.directed) this.edges.set(JSON.stringify([b, a]), { a: b, b: a, weight });
  }
  /**
   * 删除具有指定键的节点
   * @param key
   */
  removeNode(key: string) {
    this.nodes = this.nodes.filter((n: { key: string }) => n.key !== key);
    [...this.edges.values()].forEach(({ a, b }) => {
      if (a.key === key || b.key === key) this.edges.delete(JSON.stringify([a, b]));
    });
  }
  /**
   * 删除两个给定节点之间的边
   * @param a
   * @param b
   */
  removeEdge(a: any, b: any) {
    this.edges.delete(JSON.stringify([a, b]));
    if (!this.directed) this.edges.delete(JSON.stringify([b, a]));
  }
  /**
   * 检索具有给定键的节点
   * @param key
   * @returns
   */
  findNode(key: string) {
    return this.nodes.find((x: { key: string }) => x.key === key);
  }
  /**
   * 检查图在两个给定节点之间是否有边
   * @param a
   * @param b
   * @returns
   */
  hasEdge(a: any, b: any) {
    return this.edges.has(JSON.stringify([a, b]));
  }
  /**
   * 设置给定边的权重
   * @param a
   * @param b
   * @param weight
   */
  setEdgeWeight(a: any, b: any, weight: any) {
    this.edges.set(JSON.stringify([a, b]), { a, b, weight });
    if (!this.directed) this.edges.set(JSON.stringify([b, a]), { a: b, b: a, weight });
  }
  /**
   * 获取给定边的权重
   * @param a
   * @param b
   * @returns
   */
  getEdgeWeight(a: any, b: any) {
    return this.edges.get(JSON.stringify([a, b]))?.weight;
  }
  /**
   * 从给定节点查找存在边的所有节点
   * @param key
   * @returns
   */
  adjacent(key: string) {
    return [...this.edges.values()].reduce((acc, { a, b }) => {
      if (a.key === key) acc.push(b);
      return acc;
    }, [] as GraphNode[]);
  }
  /**
   * 计算给定节点的总边数
   * @param key
   * @returns
   */
  inDegree(key: string) {
    return [...this.edges.values()].reduce((acc, { a, b }) => (b.key === key ? acc + 1 : acc), 0);
  }
  /**
   * 计算给定节点的总边数
   * @param key
   * @returns
   */
  outDegree(key: string) {
    return [...this.edges.values()].reduce((acc, { a, b }) => (a.key === key ? acc + 1 : acc), 0);
  }
}

3.3 深度优先搜索和广度优先搜索

深度优先搜索 (DFS) 是一种用于遍历或搜索树或图数据结构的算法。一个从根开始（在图的情况下选择某个任意节点作为根）并在回溯之前沿着每个分支尽可能地探索。

广度优先搜索 (BFS) 则是从树根（或图的某个任意节点，有时称为“搜索key”）开始，首先探索邻居节点，然后再移动到下一级邻居。

3.4 剑指 offer 搜索题（typescript 版）

矩阵中的路径

机器人的运动范围

4 堆

4.1 堆的基本操作

堆是具有以下性质的完全二叉树，有两种堆：

        大顶堆（大根堆）：每个节点值大于等于左、右孩子节点的值，大根堆的堆顶是整个堆中的最大元素。

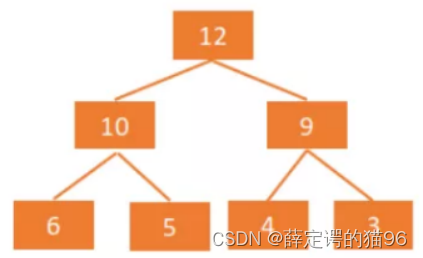
        小顶堆（小根堆）：每个节点值小于等于左、右孩子节点的值，小根堆的堆顶是整个堆中的最小元素。

存储形式：数组

应用：优先级队列（多个定时器任务问题）、求前n个最大/最小的数。

堆的基本操作包括（均依赖于堆的自我调整使其满足大/小根堆特性）：

1. 插入节点：插入位置是在堆的末尾，然后对该节点进行上浮操作（上浮即和它的父节点比较大小）；
2. 删除节点：删除位置在堆顶，然后将堆尾元素放到堆顶，对此元素进行下沉操作（下沉即和它的左、右孩子比较大小），不断递归，直到无法下沉；
3. 构建堆：把一个无序的完全二叉树调整为大/小根堆，从下往上、从左往右的对所有非叶子节点进行下沉操作。

4.2 设计堆

利用数组，实现具有插入，删除操作的大根或小根堆。

class Heap {
  container: number[];
  cmp: Function;
  /**
   * 默认是大顶堆
   * @param type
   */
  constructor(type: 'max' | 'min' = 'max') {
    this.container = [];
    this.cmp = type === 'max' ? (x, y) => x > y : (x, y) => x < y;
  }
  /**
   * 对堆中的两个节点进行交换
   * @param i
   * @param j
   */
  swap(i: number, j: number) {
    [this.container[i], this.container[j]] = [this.container[j], this.container[i]];
  }
  /**
   * 插入节点，在堆末尾插入，并对节点进行上浮操作
   * @param data
   * @returns
   */
  insert(data: number) {
    this.container.push(data);
    // 上浮操作
    let index = this.container.length - 1;
    while (index) {
      // 直到遍历到堆顶
      // 父节点位置
      const parent = Math.floor((index - 1) / 2);
      if (!this.cmp(this.container[index], this.container[parent])) {
        // 大顶堆：当前节点不大于父节点，到达最终位置
        return;
      }
      // 交换
      this.swap(index, parent);
      index = parent;
    }
  }
  /**
   * 删除节点，删除堆顶元素与堆尾元素后的堆尾所在元素，再对堆顶元素执行下沉操作
   * @returns
   */
  delete(): number {
    if (this.isEmpty()) return NaN;
    // 将堆顶元素与堆尾元素进行交换，并删除堆尾元素
    const size = this.getSize();
    this.swap(0, size - 1);
    const top = this.container.pop()!;
    // 当前节点位置
    let index = 0;
    // 交换节点位置，大顶堆：子节点中的较大者
    let exchange = index * 2 + 1;
    while (exchange < size) {
      // 右子节点位置
      let right = index * 2 + 2;
      if (right < length && this.cmp(this.container[right], this.container[exchange])) {
        // 大顶堆：存在右节点且右节点较大
        exchange = right;
      }
      if (!this.cmp(this.container[exchange], this.container[index])) {
        // 大顶堆：子节点较大者小于当前节点
        return NaN;
      }
      // 交换
      this.swap(exchange, index);
      index = exchange;
      exchange = index * 2 + 1;
    }
    return top;
  }
  /**
   * 获取堆顶元素，堆空则返回 NaN
   * @returns
   */
  top(): number {
    if (this.isEmpty()) return NaN;
    return this.container[0];
  }
  /**
   * 判断堆是否为空
   * @returns
   */
  isEmpty(): boolean {
    return this.getSize() === 0;
  }
  /**
   * 堆中元素个数
   * @returns
   */
  getSize(): number {
    return this.container.length;
  }
}

4.3 剑指 offer 堆算法题（ typescript 版）

数据流中的中位数

5 散列表

5.1 Hash表的基本操作

Hash表是一种是使用哈希函数来组织数据，支持快速插入和搜索的线性数据结构。关键是通过哈希函数将键映射到存储桶。哈希函数的选取取决于键的值范围和桶的数量。

        a) 插入新的键，哈希函数计算被存储的桶；

        b) 搜索一个键，使用相同的哈希函数计算所在桶， 然后在桶中搜索。

5.2 设计Hash表

关键是选择哈希函数和进行冲突处理

哈希函数：分配一个地址存储值。理想情况下，每个键都应该有一个对应唯一的散列值。

冲突处理：哈希函数的本质就是从 A 映射到 B。但是多个 A 键可能映射到相同的 B。

将哈希key转换为字符串的函数如下：

/**
 * @description: 将 item 也就是 key 统一转换为字符串
 */
export function defaultToString(item: any): string {
  // 对于 null undefined和字符串的处理
  if (item === null) {
    return 'NULL';
  } else if (item === undefined) {
    return 'UNDEFINED';
  } else if (typeof item === 'string' || item instanceof String) {
    return `${item}`;
  }
  // 其他情况时调用数据结构自带的 toString 方法
  return item.toString();
}

冲突解决策略：

        1） 单独链接法（链表法）：对于相同的散列值，我们将它们放到一个桶中，每个桶是相互独立的

// 单独链接法（链表）
export class HashTableSeparateChaining<K, V> {
  protected table: Map<number, MyLinkedList<{ key: K; value: V }>>;

  constructor(protected toStrFn: (key: K) => string = defaultToString) {
    this.table = new Map();
  }

  /**
   * @description: 哈希函数（djb2函数（或者loselose函数）
   */
  private hashCodeHelper(key: K): number {
    if (typeof key === 'number') {
      return key;
    }
    const tableKey = this.toStrFn(key);
    let hash = 5381;
    for (let i = 0; i < tableKey.length; i++) {
      hash = hash * 33 + tableKey.charCodeAt(i);
    }
    return hash % 1013;
  }
  /**
   * @description: 哈希函数封装
   */
  hashCode(key: K): number {
    return this.hashCodeHelper(key);
  }
  /**
   * @description: 更新散列表
   */
  put(key: K, value: V): boolean {
    if (key !== null && value !== null) {
      const position = this.hashCode(key);
      // 当该 hashcode 不存在时，先创建一个链表
      if (this.table.get(position) == null) {
        this.table.set(position, new MyLinkedList<{ key: K; value: V }>());
      }
      // 再给链表push值
      this.table.get(position)!.addAtTail({ key, value });
      return true;
    }
    return false;
  }
  /**
   * @description: 根据键获取值
   */
  get(key: K): V | undefined {
    const position = this.hashCode(key);
    const linkedList = this.table.get(position);
    if (linkedList && linkedList.size !== 0) {
      let current = linkedList.head;
      // 去链表中迭代查找键值对
      while (current !== null) {
        if (current.val.key === key) {
          return current.val.value;
        }
        current = current.next;
      }
    }
  }
  /**
   * @description: 根据键移除值
   */
  remove(key: K): boolean {
    const position = this.hashCode(key);
    const linkedList = this.table.get(position);
    if (linkedList && linkedList.size !== 0) {
      let current = linkedList.head;
      let index = 0;
      while (current !== null) {
        if (current.val.key === key) {
          break;
        }
        index = index + 1;
        current = current.next;
      }
      linkedList.deleteAtIndex(index);
      // 关键的一点，当链表为空以后，需要在 table 中删除掉 hashcode
      if (linkedList.size === 0) {
        this.table.delete(position);
      }
      return true;
    }
    return false;
  }
  /**
   * @description: 返回是否为空散列表
   */
  isEmpty(): boolean {
    return this.size() === 0;
  }
  /**
   * @description: 散列表的大小
   */
  size(): number {
    let count = 0;
    // 迭代每个链表，累计求和
    for (const [hashCode, linkedList] of this.table) {
      count += linkedList.size;
    }
    return count;
  }
  /**
   * @description: 清空散列表
   */
  clear() {
    this.table.clear();
  }
  /**
   * @description: 返回内部table
   */
  getTable() {
    return this.table;
  }
  /**
   * @description: 替代默认的toString
   */
  toString(): string {
    if (this.isEmpty()) {
      return '';
    }
    let objStringList: string[] = [];
    for (const [hashCode, linkedList] of this.table) {
      let node = linkedList.head;
      while (node) {
        objStringList.push(`{${node.val.key} => ${node.val.value}}`);
        node = node.next;
      }
    }
    return objStringList.join(',');
  }
}

        2） 开放地址法（线性探测）：每当有碰撞，则根据我们探查的策略找到一个空的槽为止。

// 开放地址法（线性探测）
export default class HashTableLinearProbing<K, V> {
  protected table: Map<number, { key: K; value: V }>;
  constructor(protected toStrFn: (key: K) => string = defaultToString) {
    this.table = new Map();
  }
  /**
   * @description: 哈希函数（djb2函数（或者loselose函数））
   */
  private hashCodeHelper(key: K): number {
    if (typeof key === 'number') {
      return key;
    }
    const tableKey = this.toStrFn(key);
    let hash = 5381;
    for (let i = 0; i < tableKey.length; i++) {
      hash = hash * 33 + tableKey.charCodeAt(i);
    }
    return hash % 1013;
  }
  /**
   * @description: 哈希函数封装
   */
  hashCode(key: K): number {
    return this.hashCodeHelper(key);
  }
  /**
   * @description: 更新散列表
   */
  put(key: K, value: V): boolean {
    if (key !== null && value !== null) {
      const position = this.hashCode(key);
      if (this.table.get(position) == null) {
        // 当hashcode位置为空时，可以直接添加
        this.table.set(position, { key, value });
      } else {
        // 否则需要迭代查找最近的空位置再添加
        let index = position + 1;
        while (this.table.get(index) !== null) {
          index++;
        }
        this.table.set(index, { key, value });
      }
      return true;
    }
    return false;
  }
  /**
   * @description: 根据键获取值
   */
  get(key: K): V | undefined {
    const position = this.hashCode(key);
    if (this.table.get(position)) {
      // 如果查到的hashcode位置就是要查的key，则直接返回
      if (this.table.get(position)!.key === key) {
        return this.table.get(position)!.value;
      }
      // 否则需要迭代着向下查找
      let index = position + 1;
      while (this.table.get(index) != null && this.table.get(index)!.key !== key) {
        index++;
      }
      if (this.table.get(index) !== null && this.table.get(index)!.key === key) {
        return this.table.get(position)!.value;
      }
    }
    // 最后也没查到，就返回 undefined
    return undefined;
  }
  /**
   * @description: 根据键移除值
   */
  remove(key: K): boolean {
    const position = this.hashCode(key);
    if (this.table.get(position)) {
      // 同理，如果hashcode对应位置就是要查的key，则直接删除
      if (this.table.get(position)!.key === key) {
        this.table.delete(position);
        // 删除后处理副作用
        this.verifyRemoveSideEffect(key, position);
        return true;
      }
      // 同理，如果hashcode对应的位置不是要查的key，就迭代查到
      let index = position + 1;
      while (this.table.get(index) !== null && this.table.get(index)!.key !== key) {
        index++;
      }
      if (this.table.get(index) !== null && this.table.get(index)!.key === key) {
        this.table.delete(index);
        // 同样在删除后处理副作用
        this.verifyRemoveSideEffect(key, index);
        return true;
      }
    }
    return false;
  }
  /**
   * @description: 处理移除键值对后的副作用
   */
  private verifyRemoveSideEffect(key: K, removedPosition: number) {
    const hash = this.hashCode(key);
    let index = removedPosition + 1;
    // 迭代着处理后面的每一个键值对
    while (this.table.get(index) !== null) {
      const posHash = this.hashCode(this.table.get(index)!.key);
      // 挨个向前挪动，关键点在于，hashcode值比较小的键值对尽量先向前补位
      // 详细的说：如果当前元素的 hash 值小于或等于原始的 hash 值
      // 或者当前元素的 hash 值小于或等于 removedPosition（也就是上一个被移除 key 的 hash 值），
      // 表示我们需要将当前元素移动至 removedPosition 的位置
      if (posHash <= hash || posHash <= removedPosition) {
        this.table.set(removedPosition, this.table.get(index)!);
        this.table.delete(index);
        removedPosition = index;
      }
      index++;
    }
  }
  /**
   * @description: 返回是否为空散列表
   */
  isEmpty(): boolean {
    return this.size() === 0;
  }
  /**
   * @description: 散列表的大小
   */
  size(): number {
    return this.table.size;
  }
  /**
   * @description: 清空散列表
   */
  clear() {
    this.table.clear();
  }
  /**
   * @description: 返回内部table
   */
  getTable(): Map<number, { key: K; value: V }> {
    return this.table;
  }
  /**
   * @description: 替代默认的toString
   */
  toString(): string {
    if (this.isEmpty()) {
      return '';
    }
    let objStringList: string[] = [];
    for (const [hashCode, { key, value }] of this.table) {
      objStringList.push(`{${key} => ${value}}`);
    }
    return objStringList.join(',');
  }
}

        上述实现中使用到的 djb2函数（或者loselose函数），原理是借助字符串各个位上的 UTF-16 Unicode 值进行计算，然后对 特定值取余即为哈希值。

        3） 双散列法：使用两个哈希函数计算散列值，选择碰撞更少的地址。

JavaScript内置哈希表的典型设计是：

键值可以是任何具有可哈希码（映射函数获取存储区索引）的可哈希化的类型。每个桶包含一个数组，用于在初始时将所有值存储在同一个桶中。 如果在同一个桶中有太多的值，这些值将被保留在一个高度平衡的二叉树搜索树（BST）中。

插入和搜索的平均时间复杂度仍为 O(1)。最坏情况下插入和搜索的时间复杂度是 O(logN)。使用高度平衡的 BST是在插入和搜索之间的一种权衡。