文章目录
- 123. 买卖股票的最佳时机 III
- 题目解析
- 零笔交易
- 一笔交易
- 两笔交易
- 状态转移方程
- f[i][j]状态转移方程
- g[i][j]状态转移方程
- 初始化
- 完整代码
- 188. 买卖股票的最佳时机 IV
- 题目解析
- 状态转移方程
- f[i][j]状态转移方程
- g[i][j]状态转移方程
- 初始化
- 完整代码
- 53. 最大子数组和
- 状态转移方程
- 初始化
- 完整代码
123. 买卖股票的最佳时机 III
点击查看:买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
题目解析
相对于之前的股票问题,去除了手续费和冷冻期,其他大部分相同,
但是交易的次数从一次可以变为两次(最多为两次,也可以选择一次或者零次)
从买入股票到 卖出股票 ,才算完成一笔交易
零笔交易
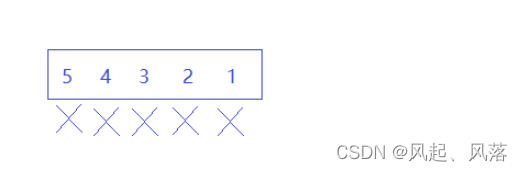
由于价格是降序的,所以无论什么时候买股票,再卖出股票都是会亏本的
所以在这个期间内,什么都不做,此时的利润为:0
此时完成零笔交易
一笔交易

当价格为升序的时候,在第一天卖出股票,在价格为5之前什么都不做,
在价格为5时,卖出股票,此时 利润为:5-1=4
此时完成 一笔交易
两笔交易
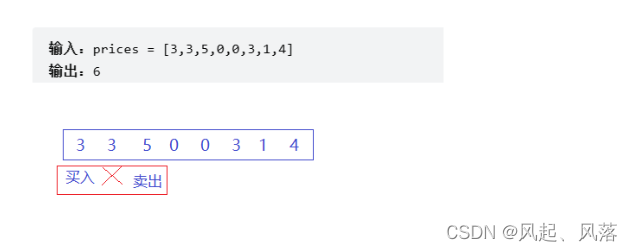
在第一天买入股票,由于第二天要是买的话根本没有利润,所以第二天什么都不做
在第三天的时候,将股票卖出 ,此时的利润为: 5-3=2
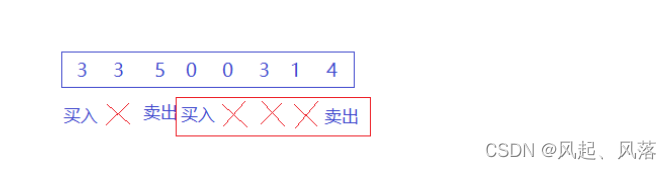
在第四天买入股票,一直到 价格为4块之前都处于什么都不干的状态
在价格为4块时,卖出股票
此时的利润为:4-0=4
完成两笔交易的总利润为:4+2=6
此时完成两笔交易
状态转移方程
dp[i]:表示第i天结束后,所能获得的最大利润
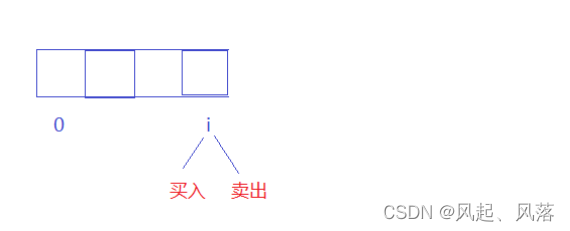
在i位置处,共有两种状态,买入状态和卖出状态
用f表示买入状态,用g表示卖出状态
通过i表示第i天结束
通过j表示交易次数
f[i][j]:表示从第i天结束后,完成了j笔交易,处于买入状态,此时的最大利润
g[i][j]:表示从第i天结束后,完成了j笔交易,处于卖出状态,此时的最大利润
在完成 买入股票,卖出股票的操作后,会改变交易次数
f[i][j]状态转移方程

若第i-1天为买入状态,则第i天啥也不干,第i天也为买入状态
该情况下:f[i][j]=f[i-1][j];

若第i-1天为卖出状态,则第i天为买入状态
需要减去买股票对应的花费 price[i]
该情况下: f[i][j]=g[i-1][j]-price[i];
状态转移方程为:
f[i][j]=max(f[i-1][j],g[i-1][j]-price[i]);
g[i][j]状态转移方程

若第i-1天为卖出状态,则第i天什么都不干,则第i天也为卖出状态
该情况下:g[i][j]=g[i-1][j];

若第i-1天为买入状态,则第i天为卖出状态
需要加上卖股票对应的利润 price[i] ,
因为完成了 从 买入到卖出的状态,第i天的交易次数+1 即变为 j,此时的j属于在原来的次数上+1
而第i-1天的交易次数依旧为原来的次数 ,所以应为 j-1
从买入股票到 卖出股票 ,才算完成一笔交易
假设j为0,则第i-1天买入股票,交易次数为0次
而第i天卖出股票,交易次数为1次
该情况下:g[i][j]=f[i-1][j-1]+price[i];
状态转移方程为:
g[i][j]= max(g[i-1][j],f[i-1][j-1]+price[i]);
初始化
对于g[i][j]的状态转移方程,当j为0时,在第i-1天完成-1笔交易,这种情况是不存在的
所以可以对g[i][j]的状态转移方程进行修改
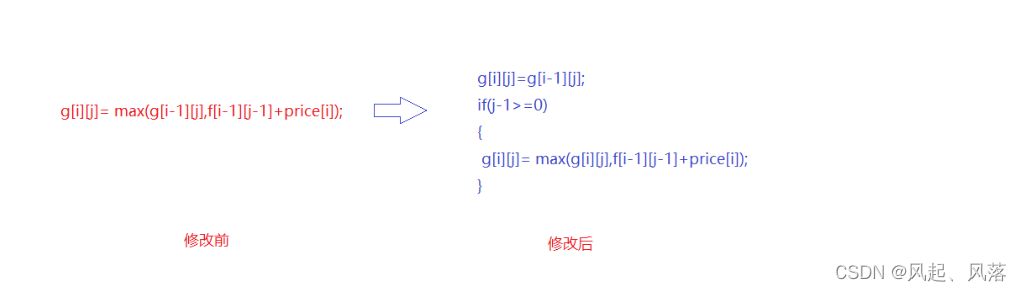
在第一步中,将g[i][j]赋值为 g[i-1][j],所以在if循环中直接将g[i-1][j]替换成g[i][j]
这样就能避免 出现-1笔交易的发生
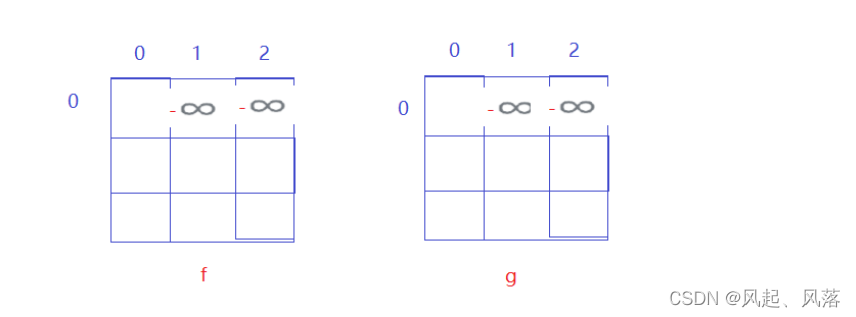
纵坐标表示 第i天结束之后
横坐标 表示 完成 i笔交易
当 纵坐标取0时,表示第0天结束之后 ,完成 0 /1/ 2笔交易,这种情况是不存在的
当天买了又卖,是没有任何利润的,而交易次数又是有限的,
所以为了不干扰后续结果,所以将第0天结束之后 ,完成 1/ 2笔交易时都设置为 负无穷大
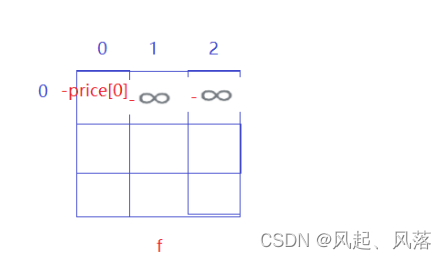
f[0][0] :表示第0天结束之后,处于买入状态,即将股票买了,需要花钱,利润为负
f[0][0]=-price[0];
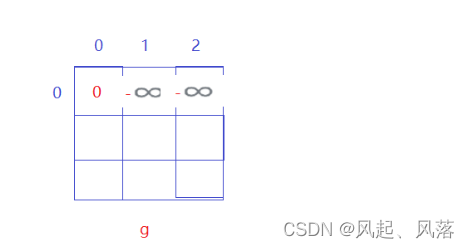
g[0][0]:表示第0天结束之后,处于卖出状态 (第0天结束之后,没有股票在手里,无法卖出,相当于啥也没干,利润为0)
g[0][0]=0;
若负无穷大 选择 INT_MIN ,则会发生越界问题
负无穷大 选择 -0x3f3f3f3f ( 0x3f3f3f3f 为int的最大值的一半)
完整代码
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n=prices.size();
//因为可能完成 0 1 2 三笔交易其中一种 所以定义为3列
//负无穷大 若要设置为INT_MIN会发生越界问题
//所以使用 -0x3f3f3f
vector<vector<int>>f(n,vector<int>(3,-0x3f3f3f3f));
vector<vector<int>>g(n,vector<int>(3,-0x3f3f3f3f));
int i=0;
int j=0;
//初始化
f[0][0]=-prices[0];
g[0][0]=0;
for(i=1;i<n;i++)
{
for(j=0;j<3;j++)
{
f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);
//修改后的状态转移方程
g[i][j]=g[i-1][j];
if(j-1>=0)
{
g[i][j]=max(g[i][j],f[i-1][j-1]+prices[i]);
}
}
}
int ret=INT_MIN;
//寻找最后一行g的最大值
for(j=0;j<3;j++)
{
if(ret<g[n-1][j])
{
ret=g[n-1][j];
}
}
//返回最后一行g的最大值
return ret;
}
};
返回值
由于 最大利润 有可能为 0笔交易/1一笔交易/2笔交易
若使用f ,则为达到最后位置,还在买入状态,不可能是最大利润
所以使用 g ,并统计 g的最后一行(0,1,2位置)的最大值
188. 买卖股票的最佳时机 IV
点击查看:买卖股票的最佳时机 IV
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格,和一个整型 k 。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1]
输出:2
解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3]
输出:7
解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
题目解析
该题与买卖股票的最佳时机 III 基本类似,只不过把之前的 最多2次(0 1 2 三种可能) 变为了 k次( [0,k-1] 种可能

k为2,表示 最多进行2笔交易(0笔交易/1笔交易 /2笔交易 三种可能) 求最大利润
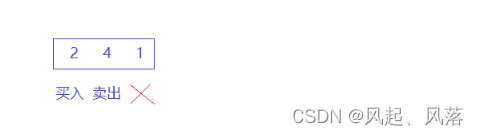
在第一天时买入股票,在第二天卖出股票,此时的利润为:4-2=2
第三天因为是最后一天,所以啥也不干
即 最大利润为:2
状态转移方程
(最佳时机IV这道题与 最佳时机III 在分析阶段 ,基本都是一致的)
dp[i]:表示第i天结束后,所能获得的最大利润
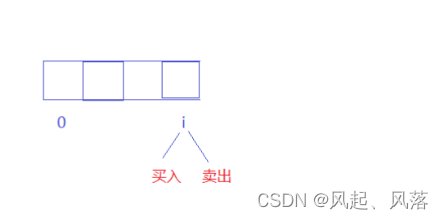
在i位置处,共有两种状态,买入状态和卖出状态
用f表示买入状态,用g表示卖出状态
通过i表示第i天结束
通过j表示交易次数
f[i][j]:表示从第i天结束后,完成了j笔交易,处于买入状态,此时的最大利润
g[i][j]:表示从第i天结束后,完成了j笔交易,处于卖出状态,此时的最大利润
在完成 买入股票,卖出股票的操作后,会改变交易次数
f[i][j]状态转移方程

若第i-1天为买入状态,则第i天啥也不干,第i天也为买入状态
该情况下:f[i][j]=f[i-1][j];

若第i-1天为卖出状态,则第i天为买入状态
需要减去买股票对应的花费 price[i]
该情况下: f[i][j]=g[i-1][j]-price[i];
状态转移方程为:
f[i][j]=max(f[i-1][j],g[i-1][j]-price[i]);
g[i][j]状态转移方程

若第i-1天为卖出状态,则第i天什么都不干,则第i天也为卖出状态
该情况下:g[i][j]=g[i-1][j];
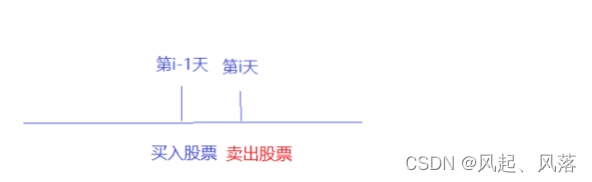
若第i-1天为买入状态,则第i天为卖出状态
需要加上卖股票对应的利润 price[i] ,
因为完成了 从 买入到卖出的状态,第i天的交易次数+1 即变为 j,此时的j属于在原来的次数上+1
而第i-1天的交易次数依旧为原来的次数 ,所以应为 j-1
从买入股票到 卖出股票 ,才算完成一笔交易
假设j为0,则第i-1天买入股票,交易次数为0次
而第i天卖出股票,交易次数为1次
该情况下:g[i][j]=f[i-1][j-1]+price[i];
状态转移方程为:
g[i][j]= max(g[i-1][j],f[i-1][j-1]+price[i]);
初始化
对于g[i][j]的状态转移方程,当j为0时,在第i-1天完成-1笔交易,这种情况是不存在的
所以可以对g[i][j]的状态转移方程进行修改

在第一步中,将g[i][j]赋值为 g[i-1][j],所以在if循环中直接将g[i-1][j]替换成g[i][j]
这样就能避免 出现-1笔交易的发生
假设k为2,则有 0笔交易 1笔交易 2笔交易 三种情况

纵坐标表示 第i天结束之后
横坐标 表示 完成 i笔交易
当 纵坐标取0时,表示第0天结束之后 ,完成 0 /1/ 2笔交易,这种情况是不存在的
当天买了又卖,是没有任何利润的,而交易次数又是有限的,
所以为了不干扰后续结果,所以将第0天结束之后 ,完成 1/ 2笔交易时都设置为 负无穷大
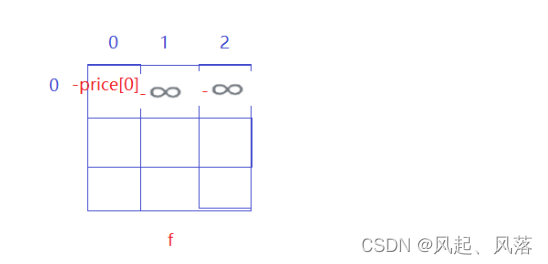
f[0][0] :表示第0天结束之后,处于买入状态,即将股票买了,需要花钱,利润为负
f[0][0]=-price[0];

g[0][0]:表示第0天结束之后,处于卖出状态 (第0天结束之后,没有股票在手里,无法卖出,相当于啥也没干,利润为0)
g[0][0]=0;
若负无穷大 选择 int_min ,则会发生越界问题
负无穷大 选择 -0x3f3f3f3f( 0x3f3f3f3f 为int的最大值的一半)\
完整代码
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
int n=prices.size();
//将k进行优化
k=min(k,n/2);
//f 表示买入状态 g表示卖出状态
//有[0,k-1] 笔交易
vector<vector<int>>f(n,vector<int>(k+1,-0x3f3f3f));
vector<vector<int>>g(n,vector<int>(k+1,-0x3f3f3f));
//初始化
f[0][0]=-prices[0];
g[0][0]=0;
int i=0;
int j=0;
for(i=1;i<n;i++)
{
for(j=0;j<=k;j++)
{
f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);
//修改后的状态转移方程
g[i][j]=g[i-1][j];
if(j-1>=0)
{
g[i][j]=max(g[i][j],f[i-1][j-1]+prices[i]);
}
}
}
//寻找g的最后一行的最大值
int ret=INT_MIN;
for(j=0;j<=k;j++)
{
if(ret<g[n-1][j])
{
ret=g[n-1][j];
}
}
//返回g的最后一行的最大值
return ret;
}
};
若有20天, k(交易次数)为30,
而最多交易只有10次,所以将k进行优化
k=min(k,n/2);
(n/2 代表最多进行交易的次数)
53. 最大子数组和
点击查看:最大子数组和
状态转移方程
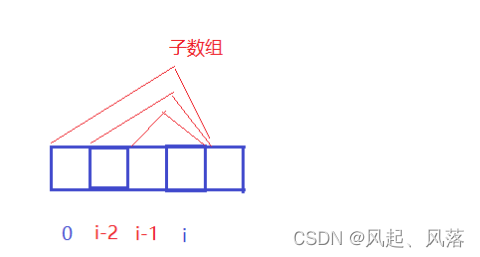
将以i为结尾的所有子数组拿到,如:i位置处本身、i与i-1位置结合、i与i-2位置结合、i与下标0位置处结合 等生成的子数组
取其中和最大的那个
dp[i]:表示以i位置元素为结尾的所有子数组中的最大和
dp[i]可被划分为两类 :
1.i位置元素本身(长度为1)
该情况下:dp[i]= nums[i]
2.i位置元素与前面元素结合(长度大于1)
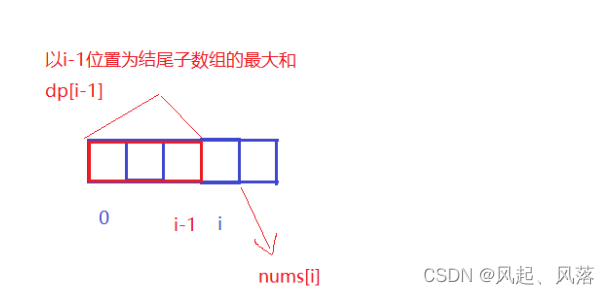
因为要求的是以i位置为结尾的子数组最大和,所以应该先求 以i-1位置为结尾的子数组的最大和 即 dp[i-1]
在加上nums[i] ,就为以i位置为结尾的子数组最大和
该情况下:dp[i]=dp[i-1]+nums[i];
初始化
若i为0时,就为发生越界问题
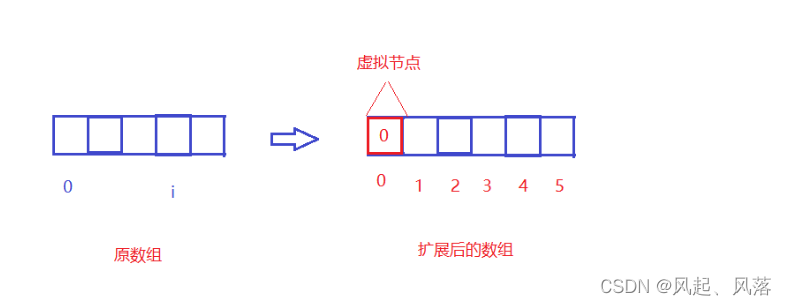
为了防止这种越界问题出现,所以加入一个虚拟节点
扩展后的数组,虚拟节点处下标为0,则 原数组的元素下标从1开始
若为dp[1],dp[1]=max(nums[1],dp[0]+nums[1])
为了保证不干扰结果,则将dp[0]的值置为0
完整代码
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n=nums.size();
//dp作为扩展数组 所以比原数组大1
vector<int>dp(n+1,0);
int i=0;
//因为dp表可能都为负,所以初始值为最小值
int ret=INT_MIN;
for(i=1;i<n+1;i++)
{
//当前下标i作为扩展数组dp的下标
//想要使用dp下标 找到对应 原数组nums对应值
//应该使用i-1
dp[i]=max(nums[i-1],dp[i-1]+nums[i-1]);
//寻找dp表的最大值
if(ret<dp[i])
{
ret=dp[i];
}
}
return ret;
}
};