前情回顾：
动态规划(4)：01背包问题详解

分割等和子集

力扣传送门：
https://leetcode.cn/problems/partition-equal-subset-sum/

题目描述：

给你一个整数数组，将这个数组里的元素分成两部分，每一部分的元素之和相等，能够被分割返回true，否则，返回零

这道题是动态规划01背包问题的一个例题，我们通过这道题可以训练一下01背包问题的变形及解法。

当然，这道题也可以采用暴力解法，即通过回溯枚举出所有子集，然后分别求出它们的和，最后再比较是否存在两个子集是相等的，当然这样做的时间复杂度很高，我们使用动态规划可以简化这道题的时间复杂度。

动态规划五步走：

1. 确定dp数组以及下标的含义
2. 递推公式的确定
3. dp数组的初始化
4. dp数组的遍历过程
5. 图例推导验证dp过程

---

首先分析：

分割数组，即意味着数组的和可以被分成两份：每份的和都是相等的，这表示可以分割这个数组：
例如：[1,5,11,5] 的总和为 22
22可以被分为 11 和 11 ，每一份的和都是11，因此只需求证每一份的和是否等于数组中和的一半就好了。

另外，如果数组的和的一半不能被整除，如21，则不能被分成两个部分，因此只需判断一下能否被整除即可判断是否返回false。

---

1. 确定dp数组以及下标的含义

我们创建dp[i][j]二维数组，其中 i 表示选择的物品编号i，j 表示的是背包的容量j。
在这道题中，我们可以把数组的某一个元素nums[i]看作物品i；然后我们把数组的元素之和看作整个背包的最大容量，那么此时 j 就表示了在容量 j 下的背包的子容量；并且我们把物品的价值也看作是元素值。

dp[i][j]：表示了容量为j的背包，把一个元素i放入了这个背包，这个背包的最大价值（最大元素和）是多少。

在本题中，我们的背包容量为 数组总和的一半（目的是为了验证dp数组的最后一个是否等于整数数组总和的一半，相等则返回true）。

 int sum=accumulate(nums.begin(), nums.end(), 0);
 if (sum%2) return false;
 int weight=sum/2;
 //初始化dp数组为和的一半
 vector<vector<int>> dp(n,vector<int>(weight+1));

---

2. 确定递推公式

在上一节中，我们详解解析了01背包问题的递推公式，在这里我们不过多解释，这道题既然可以转换为01背包的问题，那么对于此递推公式也是同样使用的。

• 把元素i 放入背包中：dp[i-1][j-nums[i]]+nums[i]

• 不把元素i 放入背包中：dp[i][j]=dp[i-1][j]

多罗嗦两句：

• . dp[i][j]=dp[i-1][j]：表示的是当前背包的容量不足以再容纳这个物品i（元素），因此无法存储此物品i，此时的价值还等于上一次的物品的价值。
• . dp[i-1][j-nums[i]]+nums[i]：表示的是：此时背包容量足够容纳这个物品，把这个物品 i 放入容量为 j - nums[i] 背包中，加上此物品的价值 nums[i]（由于在本题中是整数数组，我们假设元素大小就是物品重量，同时也是物品价值） ，即表示了我们背包的当前价值。

---

3. dp数组如何初始化

• 第一行初始化：

for (int j=nums[0];j<=weight;j++)
{
    dp[0][j]=nums[0];
}

当物品编号为0时，此时表示的就是选取了数组中第一个元素，我们的背包容量 j（j>=1），总能容纳第一个元素，所以第一行初始化为第一个元素的大小

• 第一列初始化：
  当背包的容量为0时，任何物品都不能容纳，直接第一列初始化为0，表示不能放任何编号的物品。
  由于数组的创建本身就初始化为0，所以可以不必写代码。

---

4. dp数组的遍历过程

两种方式，都可以，具体请看我的上一篇博客。

首先遍历物品（元素），然后遍历背包的容量

或者遍历背包的容量，然后遍历物品（元素）。

---

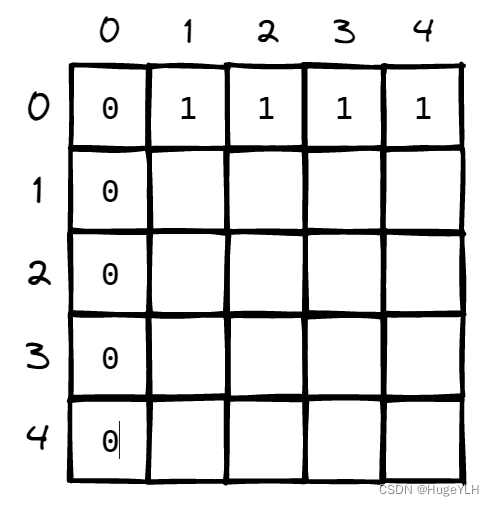
5. 图模拟dp过程：

如图：行 i，列 j，分别表示了背包容量为j时，放入物品i时的价值dp[i][j]，此时位于整个数组的最后一个元素就是我们的最大价值。

所以，我们的dp数组的最后一个元素的值等于我们的数组和的一半，因此证明了这个数组是可以被分割成等和的子集的，返回true。

---

代码示例：

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int n=nums.size();
        int m=99;
        int sum=accumulate(nums.begin(), nums.end(), 0);
        if (sum%2) return false;
        //以和的一半当作背包的总容量
        int weight=sum/2;
        vector<vector<int>> dp(n,vector<int>(weight+1));
        for (int j=nums[0];j<=weight;j++)
        {
            dp[0][j]=nums[0];
        }
        //先遍历物品，再遍历背包
        for (int i=1;i<n;i++)
        {
            for (int j=0;j<=weight;j++)
            {
                if (j<nums[i]) dp[i][j]=dp[i-1][j];
                else dp[i][j]=max(dp[i-1][j],dp[i-1][j-nums[i]]+nums[i]);
            }
        }
        //判断最后一个元素是不是和的一半
        return dp[n-1].back()==weight;
    }
};

滚动数组优化，动态规划：

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int n=nums.size();
        int sum=accumulate(nums.begin(),nums.end(),0);
        if (sum%2) return false;
        int target=sum/2;
        vector<int> dp(target+1);
        for (int i=0;i<n;i++)
        {
            for (int j=target;j>=nums[i];j--)
            {
                dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);
            }
        }
        return dp.back()==target;
    }
};

---

最后一块石头的重量

力扣传送门：
https://leetcode.cn/problems/last-stone-weight-ii/

本题不再过多描述，详细请移步leetcode。

直接解析：

既然要每次选出两块石头，然后依次两块两块进行操作，我们可以大胆的把这个石头数组分成两堆。

我们的dp数组描述其中的一堆。

和上一题完全一致：

1. 确定dp数组以及其下标的含义

dp[i][j]：表示把石头编号为i的放入背包容量为j的背包中，当前背包的最大价值（石头的总重量）。

2. 递推公式的确定

• 不放石头：dp[i][j]=dp[i-1][j]
• 放石头： dp[i][j]=dp[i-1][j-stone[i]]+stone[i]

3. dp数组的初始化

我们的背包容量j (j>=1)一定可以存储第一块石头，第一行初始化为第一块石头的重量
背包的容量为0时，无法放任何一块石头，第一列的初始化。

4. dp的遍历
5. 图例推导dp数组

---

我们dp数组最后存储的是这一堆的石头的总重量，sum - 这一堆 =另一堆，

因此

另一堆 - 这一堆 = 最后的结果

普通的动态规划：

class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        int sum=accumulate(stones.begin(),stones.end(),0);
        int target=sum/2;
        int n=stones.size();
        vector<vector<int>> dp(n,vector<int>(target+1));
        for (int j=stones[0];j<=target;j++)
        {
            dp[0][j]=stones[0];
        }
        for (int i=1;i<n;i++)
        {
            for (int j=0;j<=target;j++)
            {
                if (j<stones[i]) dp[i][j]=dp[i-1][j];
                else dp[i][j]=max(dp[i-1][j],dp[i-1][j-stones[i]]+stones[i]);
            }
        }
        //sum - dp[n-1].back()
        return sum-dp[n-1].back()-dp[n-1].back();
    }
};

滚动数组优化，动态数组：

class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        int sum=accumulate(stones.begin(),stones.end(),0);
        int target=sum/2;
        int n=stones.size();
        vector<int> dp(target+1);
        //背包重量为0时，啥也不能放
        dp[0]=0;
        for (int i=0;i<n;i++)
        {
            for (int j=target;j>=stones[i];j--)
            {
                dp[j]=max(dp[j],dp[j-stones[i]]+stones[i]);
            }
        }
        return sum-dp[target]-dp[target];
    }
};