首先我们应该熟悉numpy的矩阵取值

[:, 1::2] # 第一维，从第二个元素起步长为2取元素
[:, ::2] # 第一维，从第一个元素起步长为2取元素

1 遗传本质

染色体的交叉和变异

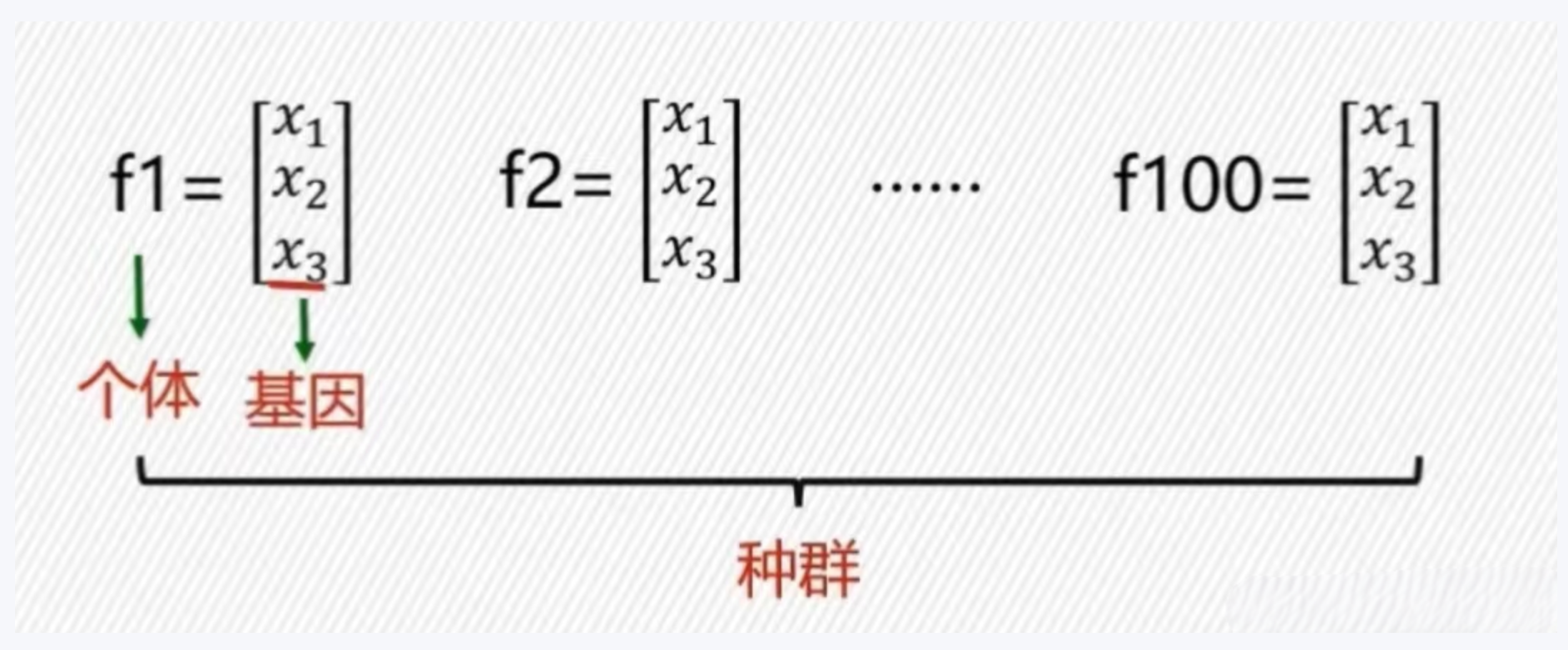
种群：很多个个体组成的群体，即为所有可能解的集合
个体：待求解优化问题的一个解，并且该解在计算机中被编码为一个向量表示
实数编码为一个向量表示
染色体：将个体编码后的二进制串，即为个体的二进制编码表示
基因：每个解的组成分量
染色体长度：变量个数

在这里插入图片描述

创建族群

交换染色体信息
染色体信息变异
族群优胜劣汰

创建随机解集

两解交换信息
选择信息变异
去除劣势的解

2 编码

二进制编码，将数值转化为二进制串，用于求解问题（一个长度为n的串，表示表示2^{n}个数）

给定值解的取值范围：[1，10]
给定精度：1e-5，两个数值解的间隔
进行编码：为每个数值解分配一个独一无二的二进制串

TSP问题，比如有10个城市，某个解可表示为[3，2，1，4，5，7，6，8，9，10]

根据不同的问题，进行不同的抽象实现

通过GA的寻优计算，求目标函数5x1 + 4x4 + 6x3的最小值

在这里插入图片描述

import numpy as np
from numpy import random
import math
import matplotlib.pyplot as plt


def fun2(x1, x2, x3):  # 适应度值的目标函数
    return 5 * x1 + 4 * x2 + 6 * x3


def code(bound):
    '''
    初始化100*3的种群，通过边界限定
    :param lenchrom:变量数
    :param bound: 边界
    :return: 最初种群
    '''
    flag = 0
    if flag == 0:
        pick_1 = random.random((1, 3))
        ret = bound[:, 0].T + (bound[:, 1] - bound[:, 0]).T * pick_1
        # flag=text(bound,ret)
    return ret

    # def text(code):
    '''

    :param code: 看code中去到的x1,x2,x3是不是大于0，小于50
    :return: 满足要求就return保留数据，继续循环
    '''
    # flag_text=1
    # for i in range(3):
    #     if int(code[i]) in np.arahge(51): # >0 or code[0]<50:
    #         print(int(code[i]))
    #         flag_text=0
    #     return flag_text


def Select(individuals, fitness, sizepop):
    '''
    选择适应度最小的族群
    :param individuals:
    :param fitness:适应度
    :param sizepop:
    :return:
    '''
    fitness = 1 / fitness
    sumfitness = sum(fitness)
    sumf = fitness / sumfitness
    index = np.zeros(100)
    for i in range(sizepop):
        pick_2 = random.random()
        if pick_2 == 0:
            pick_2 = random.random()
            for j in range(sizepop):
                pick_2 -= sumf[j]
                if pick_2 < 0:
                    index[i] = j
                    break
    for i in range(100):
        n = int(index[i])  # 将index[i]化为整数
        individuals[i, :] = individuals[n, :]
    return individuals


def Cross(pcross, lenchrom, chrom, sizepop, bound):
    '''
    交叉
    :param pcross: 交叉概率
    :param lenchrom: 变量数
    :param chrom: 经过选择后的种族
    :param sizepop: 种族数
    :param bound: 边界
    :return: 交叉后的种族
    '''
    '''   数据选择交叉的行   '''
    for i in range(100):
        pick = random.random((1, 2))
        n = pick[:, 0] * pick[:, 1]
        if n == 0:
            pick = random.random((1, 2))  # 防止产生的两个随机数中含有0
        '根据交叉概率过滤掉30%的数据'
        index1 = int(pick[:, 0] * sizepop)  # 从0开始，向下取整
        index2 = int(pick[:, 1] * sizepop)
        index = np.array([index1, index2])
        '交叉的概率'
        pick = random.random(1)
        if pick > pcross:
            continue
        '''   数据选择结束   '''
        '''   选择交叉的行数   '''
        flag = 0
        if flag == 0:
            pick = random.random(1)
        pos = int(pick * 3)  # 取交换的列
        pick = random.random(1)
        v1 = chrom[index[0], pos]
        v2 = chrom[index[1], pos]
        chrom[index[0], pos] = pick * v2 + (1 - pick) * v1
        chrom[index[1], pos] = pick * v1 + (1 - pick) * v2
    return chrom


def Mutation(pmutation, lenchrom, chrom, sizepop, i, bound):
    '''
    变异
    :param pmutation:变异概率
    :param lenchrom:变量数
    :param chrom:种族
    :param sizepop:种族大小
    :param pop:迭代次数
    :param bound:边界
    :return:变异后的种族
    '''
    pop = np.array([i, 100])
    '选择变异的行'
    for i in range(100):
        pick_1 = random.random(1)  # pick1变异行的索引
        if pick_1 == 0:
            pick_1 = random.random(1)
        index = int(pick_1 * sizepop)
        '过滤掉不变异的样本'
        pick_2 = random.random(1)
        if pick_2 > pmutation:
            continue
        flag = 0
        if flag == 0:
            pick_3 = random.random(1)
            if pick_3 == 0:
                pick_3 = random.random(1)
            pos = int(pick_3 * 3)  # 变异的列
            v = chrom[i, pos]
            v1 = v - 0
            v2 = 50 - v
            pick_4 = random.random(1)
            if pick_4 > 0.5: # 变异公式
                delta = v2 * (1 - pick_4 ** ((1 - pop[0] / pop[1]) ** 2))
                chrom[i, pos] = v + delta
            else:
                delta = v1 * (1 - pick_4 ** ((1 - pop[0] / pop[1]) ** 2))
                chrom[i, pos] = v - delta
    return chrom


'1.初始化变量'
popsize = 100  # 种群大小规模
lenchrom = 3  # 变量数（染色体长度）x1,x2,x3
pc = 0.7  # 交叉概率
pm = 0.3  # 变异概率
maxgen = 100  # 最大迭代次数,进化的次数
popmax = 50  # 变量x1 x2 x3上界
popmin = 0  # 变量下界
bound = np.array([[0, 50], [0, 50], [0, 50]])

'2.初始化粒子给设定初始种群，计算适应度'
GApop = np.zeros((100, 3))  # 返回一个元素全为0且给定形状和类型的数组，100*3的二维数组
fitness = np.zeros(100)
for i in range(100):
    GApop[i, :] = code(bound)  # 数组第一维中下标为i的元素的所有值
    x1 = GApop[i, 0]
    x2 = GApop[i, 1]
    x3 = GApop[i, 2]
    fitness[i] = fun2(x1, x2, x3)

print(fitness)

'3.寻找个体最优和各局最优'
bestfitness = min(fitness)  # 适应度最小
for i in range(100):
    if fitness[i] == bestfitness:
        break
zbest = GApop[i, :]  # 适应度最小的索引对应的个体，就是全局最优个体→个体最优
gbest = GApop  # GApop中的100个个体就是全局最优
fitnessgbest = fitness
fitnesszbest = bestfitness

'4.选择交叉变异'
yy = np.zeros(100)
for i in range(100):
    '选择'
    GApop = Select(GApop, fitness, popsize)
    '交叉'
    GApop = Cross(pc, lenchrom, GApop, popsize, bound)
    '变异'
    GApop = Mutation(pm, lenchrom, GApop, popsize, i, bound)
    pop = GApop

    '5.选满足的约束条件'
    for j in range(100):
        if pop[j, 0] - pop[j, 1] + pop[j, 2] <= 20:
            if 3 * pop[j, 0] + 2 * pop[j, 1] + 4 * pop[j, 2] <= 42:
                if 3 * pop[j, 0] + 2 * pop[j, 1] <= 30:
                    x1 = pop[j, 0]
                    x2 = pop[j, 1]
                    x3 = pop[j, 2]
                    fitness[j] = fun2(x1, x2, x3)

        '6.更新个体最优'
        if fitness[j] < fitnessgbest[j]:
            gbest[j, :] = pop[j, :]
            fitnessgbest = fitness[j]
        '7.更新总体最优'
        if fitness[j] < fitnessgbest[j]:
            zbest = pop[j, :]
            fitnesszbest = fitness[j]
        yy[i] = fitnesszbest

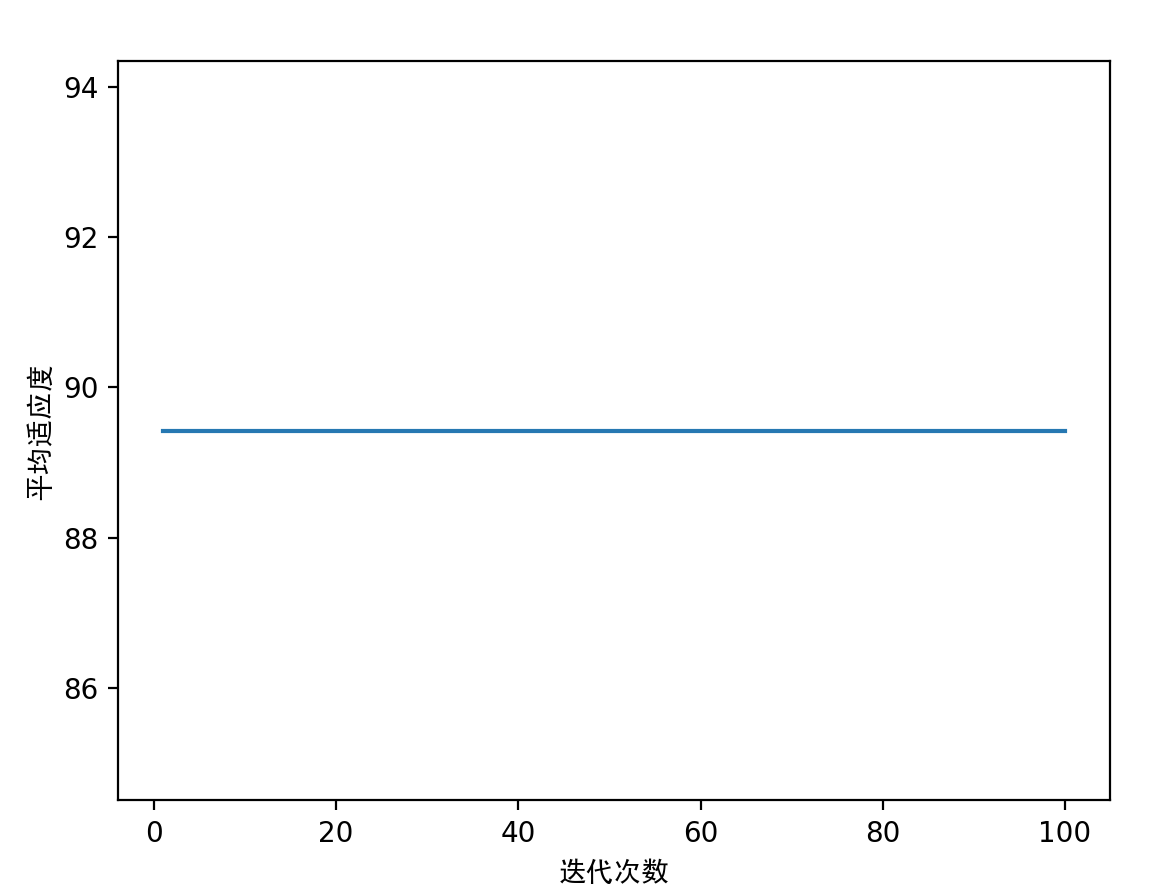
'5.画图'
x = np.arange(1, 101)
plt.plot(x, yy)
plt.xlabel('迭代次数', fontproperties='SimHei')
plt.ylabel('平均适应度', fontproperties='SimHei')
plt.show()

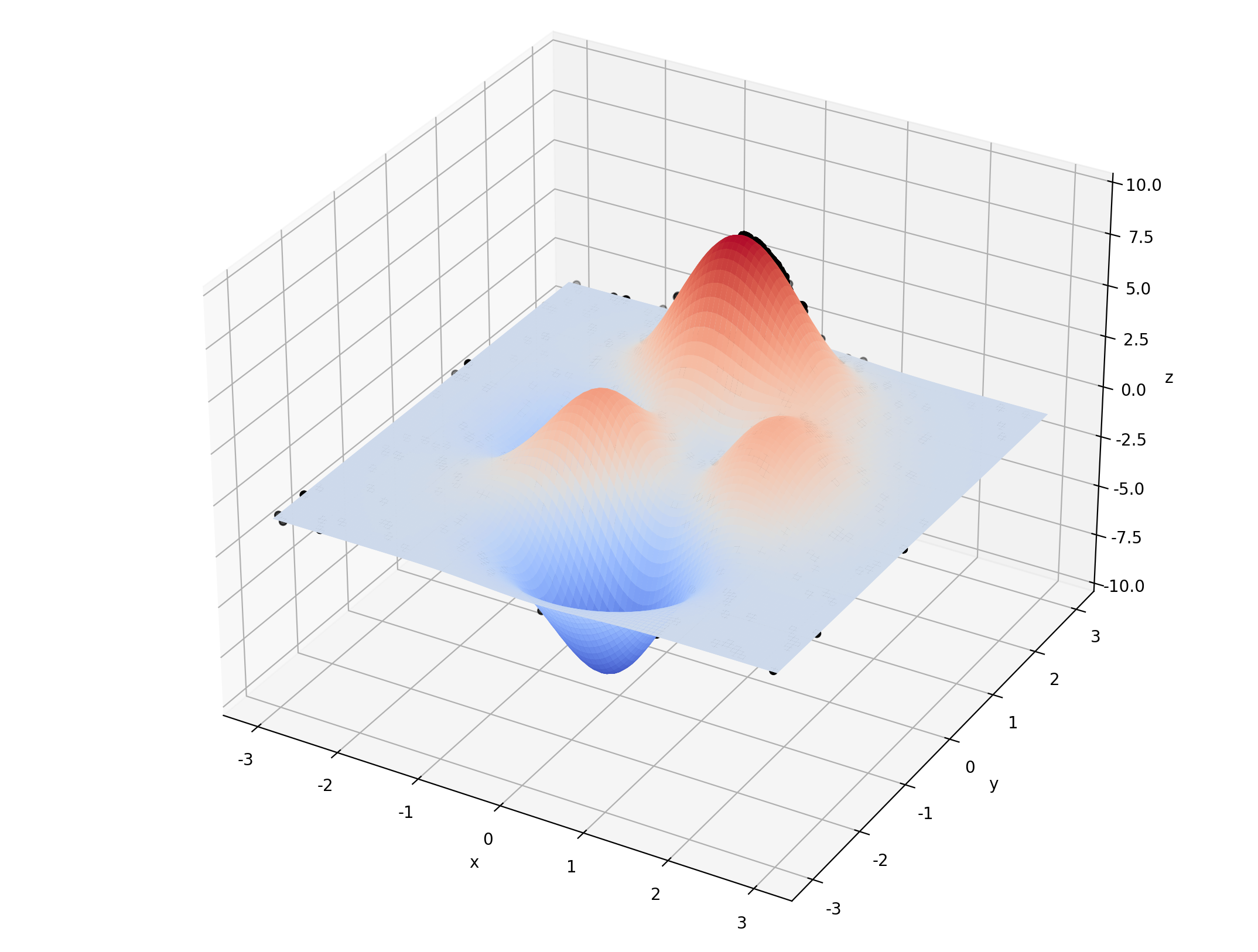
在这里插入图片描述

3.1 单目标多变量函数 - 无约束 - （可画立体图）

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

DNA_SIZE = 24  # 一个实数DNA的长度
POP_SIZE = 200 # 种族数量
CROSSOVER_RATE = 0.8 # 交叉概率
MUTATION_RATE = 0.005 # 变异概率
N_GENERATIONS = 50 # 迭代次数
X_BOUND = [-3, 3]  # x取值范围
Y_BOUND = [-3, 3]  # y取值范围


# 适应度的目标函数
def F(x, y):
    return 3 * (1 - x) ** 2 * np.exp(-(x ** 2) - (y + 1) ** 2) - 10 * (x / 5 - x ** 3 - y ** 5) * np.exp(
        -x ** 2 - y ** 2) - 1 / 3 ** np.exp(-(x + 1) ** 2 - y ** 2)


def plot_3d(ax):
    # np.linspace()生成等距数组
    X = np.linspace(*X_BOUND, 100)
    Y = np.linspace(*Y_BOUND, 100)
    X, Y = np.meshgrid(X, Y)
    Z = F(X, Y)
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
    ax.set_zlim(-10, 10)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')
    plt.pause(3)
    plt.show()


# 得到一个种群
# 设置DNA_SIZE=24（一个实数DNA长度），两个实数x , y
# x,y一共用48位二进制编码，我同时将x和y编码到同一个48位的二进制串里，每一个变量用24位表示，奇数24列为x的编码表示，偶数24列为y的编码表示
def translateDNA(pop):  # pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目
    x_pop = pop[:, 1::2]  # 奇数列表示X，第一维，从第二个元素起步长为2取元素
    y_pop = pop[:, ::2]  # 偶数列表示y

    # pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
    '''
    将【0，1】区间的数映射到需要的区间：
    x_ = num * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0] #映射为x范围内的数
    y_ = num * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0] #映射为y范围内的数
    '''
    # [::-1]取从后向前的元素
    x = x_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0]
    y = y_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]
    return x, y


# 求最小值适应度函数
def get_fitness(pop):
    x, y = translateDNA(pop)
    # 将可能解带入函数F中得到的预测值
    pred = F(x, y)
    # 减去最小的适应度是为了防止适应度出现负数，通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度
    return (pred - np.min(pred)) + 1e-3


# 根据适应度选择
# 适应度越高，被选择的机会越高；适应度越低，被选择的机会越低
def select(pop, fitness):  # nature selection wrt pop's fitness
    # p描述了从np.arange(POP_SIZE)里选择每一个元素的概率，概率越高越容易被选中
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True, p=fitness / (fitness.sum()))
    return pop[idx]


# 交叉
def crossover_and_mutation(pop, CROSSOVER_RATE=0.8):
    new_pop = []
    for father in pop:  # 遍历种群中的每一个个体，将该个体作为父亲
        child = father  # 孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）
        if np.random.rand() < CROSSOVER_RATE:  # 产生子代时不是必然发生交叉，而是以一定的概率发生交叉
            mother = pop[np.random.randint(POP_SIZE)]  # 再种群中选择另一个个体，并将该个体作为母亲
            cross_points = np.random.randint(low=0, high=DNA_SIZE * 2)  # 随机产生交叉的点
            child[cross_points:] = mother[cross_points:]  # 孩子得到位于交叉点后的母亲的基因
        mutation(child)  # 每个后代有一定的机率发生变异
        new_pop.append(child)
    return new_pop


# 变异
def mutation(child, MUTATION_RATE=0.003):
    if np.random.rand() < MUTATION_RATE:  # 以MUTATION_RATE的概率进行变异
        mutate_point = np.random.randint(0, DNA_SIZE * 2)  # 随机产生一个实数，代表要变异基因的位置
        child[mutate_point] = child[mutate_point] ^ 1  # 将变异点的二进制为反转


def print_info(pop):
    fitness = get_fitness(pop)
    max_fitness_index = np.argmax(fitness)
    print("max_fitness:", fitness[max_fitness_index])
    x, y = translateDNA(pop)
    print("最优的基因型：", pop[max_fitness_index])
    print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))


if __name__ == "__main__":
    fig = plt.figure()
    ax = Axes3D(fig)
    fig.add_axes(ax)
    plt.ion()  # 将画图模式改为交互模式，程序遇到plt.show不会暂停，而是继续执行
    plot_3d(ax)

    '迭代交叉算法'
    pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 2))  # matrix (POP_SIZE, DNA_SIZE)
    for _ in range(N_GENERATIONS):  # 迭代N代
        x, y = translateDNA(pop)
        # 特征值散点图，x,y,点的大小,颜色,标记
        sca = ax.scatter(x, y, F(x, y), c='black', marker='o')
        # locals()以字典类型返回当前位置的所有局部变量
        if sca in locals():
            sca.remove()
        plt.show()
        # 动态绘制窗口
        plt.pause(0.1)
        pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE)) # 种族通过交叉变异产生后代
        # F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
        fitness = get_fitness(pop) # 对种族的每个个体进行评估
        pop = select(pop, fitness)  # 选择生成新的种群

    print_info(pop)
    plt.ioff() # 画动态图
    plot_3d(ax)
    print("over")

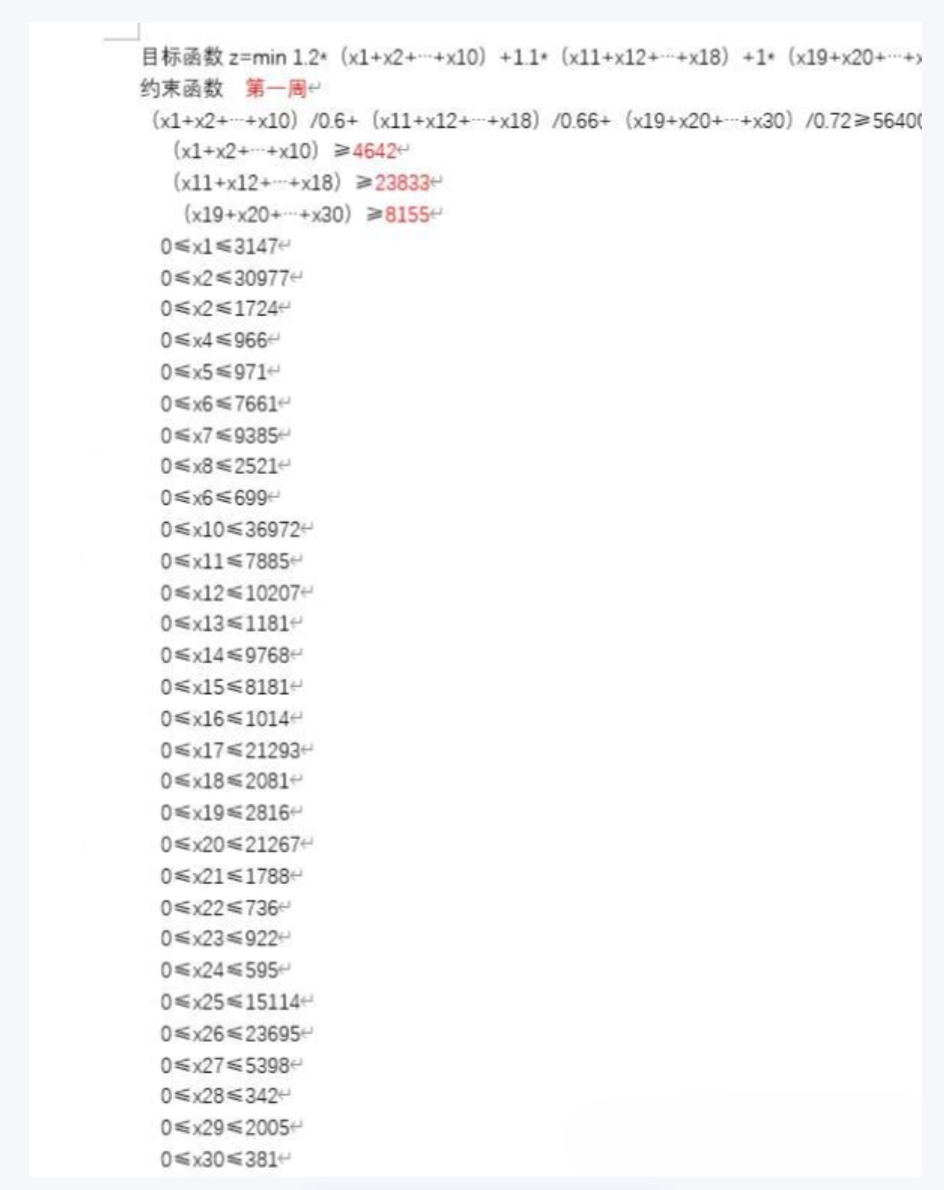
在这里插入图片描述

3.2 单目标多变量函数 - 罚算法 - 约束

在这里插入图片描述

import numpy as np
import random
import matplotlib.pyplot as plt
from deap import creator, tools, base, algorithms

# 定义问题
creator.create('FitnessMin', base.Fitness, weights=(-1.0,))
creator.create('Individual', list, fitness=creator.FitnessMin)

lb = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
up = [3147, 30977, 1724, 966, 971, 7661, 9385, 2521, 699, 36972, 7885, 10207, 1181, 9768, 8181, 1014, 21293, 2081, 2816,
      21267, 1788, 736, 922, 595, 15114, 23695, 5398, 342, 2005, 381]


def uniform(lb, up):
    return [random.uniform(a, b) for a, b in zip(lb, up)]


# 生成个体
toolbox = base.Toolbox()
toolbox.register('Attr_float', uniform, lb, up)
toolbox.register('Individual', tools.initIterate, creator.Individual, toolbox.Attr_float)

# 生成种群
pop_size = 100
toolbox.register('Population', tools.initRepeat, list, toolbox.Individual)
pop = toolbox.Population(n=pop_size)


# 评价函数
def himmelblauFun(ind):
    return (1.2 * (ind[0] + ind[1] + ind[2] + ind[3] + ind[4] + ind[5] + ind[6] + ind[7] + ind[8] + ind[9] ) +
            1.1 * (ind[10]+ind[11] + ind[12] + ind[13] + ind[14] + ind[15] + ind[16] + ind[17] + ind[18] + ind[19]  ) +
            (ind[20]+ind[21] + ind[22] + ind[23] + ind[24] + ind[25] + ind[26] + ind[27] + ind[12] + ind[29])),


# 施加约束
def feasible(ind):
    # 判定解是否可行
    g1 = (ind[0] + ind[1] + ind[2] + ind[3] + ind[4] + ind[5] + ind[6] + ind[7] + ind[8] + ind[9]) / 0.6 + (
            ind[10] + ind[11] + ind[12] + ind[13] + ind[14] + ind[15] + ind[16] + ind[17] + ind[18] + ind[
        19]) / 0.66 + (ind[20] + ind[21] + ind[22] + ind[23] + ind[24] + ind[25] + ind[26] + ind[27] + ind[28] + ind[
        29]) / 0.72
    g2 = ind[0] + ind[1] + ind[2] + ind[3] + ind[4] + ind[5] + ind[6] + ind[7] + ind[8] + ind[9]
    g3 = ind[10] + ind[11] + ind[12] + ind[13] + ind[14] + ind[15] + ind[16] + ind[17] + ind[18] + ind[19]
    g4 = ind[20] + ind[21] + ind[22] + ind[23] + ind[24] + ind[25] + ind[26] + ind[27] + ind[28] + ind[29]
    cond1 = (g1 >= 56400)
    cond2 = (g2 >= 4642)
    cond3 = (g3 >= 23833)
    cond4 = (g4 >= 8155)
    # x1 = (ind[0] >= 0) and (ind[0] <= 3147)
    # x2 = (ind[0] >= 0) and (ind[0] <= 30977)  # [0, 30977]
    # x3 = (ind[0] >= 0) and (ind[0] <= 1724)  # [0, 1724]
    # x4 = (ind[0] >= 0) and (ind[0] <= 966)  # [0, 966]
    # x5 = (ind[0] >= 0) and (ind[0] <= 971)  # [0, 971]
    # x6 = (ind[0] >= 0) and (ind[0] <= 7661)  # [0, 7661]
    # x7 = (ind[0] >= 0) and (ind[0] <= 9385)  # [0, 9385]
    # x8 = (ind[0] >= 0) and (ind[0] <= 2521)  # [0, 2521]
    # x9 = (ind[0] >= 0) and (ind[0] <= 699)  # [0, 699]
    # x10 = (ind[0] >= 0) and (ind[0] <= 36972)  # [0, 36972]
    # x11 = (ind[0] >= 0) and (ind[0] <= 7885)  # [0, 7885]
    # x12 = (ind[0] >= 0) and (ind[0] <= 10207)  # [0, 10207]
    # x13 = (ind[0] >= 0) and (ind[0] <= 1181)  # [0, 1181]
    # x14 = (ind[0] >= 0) and (ind[0] <= 9768)  # [0, 9768]
    # x15 = (ind[0] >= 0) and (ind[0] <= 8181)  # [0, 8181]
    # x16 = (ind[0] >= 0) and (ind[0] <= 1014)  # [0, 1014]
    # x17 = (ind[0] >= 0) and (ind[0] <= 21293)  # [0, 21293]
    # x18 = (ind[0] >= 0) and (ind[0] <= 2081)  # [0, 2081]
    # x19 = (ind[0] >= 0) and (ind[0] <= 2816)  # [0, 2816]
    # x20 = (ind[0] >= 0) and (ind[0] <= 21267)  # [0, 21267]
    # x21 = (ind[0] >= 0) and (ind[0] <= 1788)  # [0, 1788]
    # x22 = (ind[0] >= 0) and (ind[0] <= 736)  # [0, 736]
    # x23 = (ind[0] >= 0) and (ind[0] <= 922)  # [0, 922]
    # x24 = (ind[0] >= 0) and (ind[0] <= 595)  # [0, 595]
    # x25 = (ind[0] >= 0) and (ind[0] <= 15114)  # [0, 15114]
    # x26 = (ind[0] >= 0) and (ind[0] <= 23695)  # [0, 23695]
    # x27 = (ind[0] >= 0) and (ind[0] <= 5398)  # [0, 5398]
    # x28 = (ind[0] >= 0) and (ind[0] <= 342)  # [0, 342]
    # x29 = (ind[0] >= 0) and (ind[0] <= 2005)  # [0, 2005]
    # x30 = (ind[0] >= 0) and (ind[0] <= 381)  # [0, 381]
    if cond1 and cond2 and cond3 and cond4 :

    # if cond1 and cond2 and cond3 and cond4 and x1 and x2 and x3 and x4 and x5 and x6 and x7 and x8 and x9 and x10 and x11 and x12 and x13 and x14 and x15 and x16 and x17 and x18 and x19 and x20 and x21 and x22 and x23 and x24 and x25 and x26 and x27 and x28 and x29 and x30:
        return True
    return False


# 注册评价函数
toolbox.register('evaluate', himmelblauFun)
toolbox.decorate('evaluate', tools.DeltaPenalty(feasible, 1e3))  # death penalty

# 注册进化过程中需要的工具:配种选择，交叉，变异
toolbox.register('select', tools.selTournament, tournsize=2)  # 锦标赛
toolbox.register('mate', tools.cxSimulatedBinaryBounded, eta=20, low=lb, up=up)
toolbox.register('mutate', tools.mutPolynomialBounded, eta=20, low=lb, up=up, indpb=0.2)

# 创建统计对象
# 用数据记录算法迭代过程
stats = tools.Statistics(key=lambda ind: ind.fitness.values)
stats.register('avg', np.mean)
stats.register('std', np.std)
stats.register('min', np.min)
stats.register('max', np.max)

# 创建日志对象
logbook = tools.Logbook()

# 进化迭代，不妨设置如下参数
N_Gen = 50
CXPB = 0.8
MUTPB = 0.2

# 评价初代个体
fitnesses = map(toolbox.evaluate, pop)
for ind, fit in zip(pop, fitnesses):
    ind.fitness.values = fit
record = stats.compile(pop)
logbook.record(gen=0, **record)

# 遗传算法迭代
for gen in range(1, N_Gen + 1):
    # 配种选择
    selectTour = toolbox.select(pop, pop_size)
    # 复制个体，供交叉使用
    selectInd = list(map(toolbox.clone, selectTour))
    # print(selectInd)
    # 对选出的个体两两进行交叉，对于被改变的个体，删除其适应度
    for child1, child2 in zip(selectInd[::2], selectInd[1::2]):
        if random.random() < CXPB:
            toolbox.mate(child1, child2)
            del child1.fitness.values
            del child2.fitness.values

    # 变异
    for mutate in selectInd:
        if random.random() < MUTPB:
            toolbox.mutate(mutate)
            del mutate.fitness.values

    # 对于被改变的个体，重新计算其适应度
    invalid_ind = [ind for ind in selectInd if not ind.fitness.valid]
    fitnesses = map(toolbox.evaluate, invalid_ind)
    for ind, fit in zip(invalid_ind, fitnesses):
        ind.fitness.values = fit

    # 精英育种-环境选择
    combinedPop = pop + selectTour
    pop = tools.selBest(combinedPop, pop_size)

    # 记录数据-将stats注册功能应用于pop,并作为字典返回
    record = stats.compile(pop)
    logbook.record(gen=gen, **record)

# 输出计算过程
# logbook.header = 'gen', 'avg', 'std', 'min', 'max'
# print(logbook)

# 输出最优解
bestInd = tools.selBest(pop, 1)[0]
bestFit = bestInd.fitness.values[0]
print('当前最优解为:', str(bestInd))
# print('对应的函数最小值为:', str(bestFit))

# 打印变化值
import matplotlib.pyplot as plt

# 用select方法从logbook提取迭代次数、最大值、均值
gen = logbook.select('gen')
fitness_min = logbook.select('min')
fitness_avg = logbook.select('avg')

fig = plt.figure()
fig.add_subplot()
plt.plot(gen, fitness_avg, 'r-', label='fitness_avg')
plt.plot(gen, fitness_min, 'b-', label='fitness_min')
plt.legend(loc='best')
plt.xlabel('gen')
plt.ylabel('fitness')
plt.tight_layout()
plt.show()

4 单目标多变量函数 - 带约束

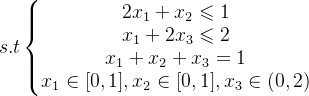
在这里插入图片描述

import numpy as np
import geatpy as ea
# from myaim import MyProblem

class MyProblem(ea.Problem):                # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'                  # 初始化name（函数名称，可以随意设置）
        M = 1                               # 初始化M（目标维数）----- 有几个目标函数
        maxormins = [-1]                    # 初始化目标最小最大化标记列表，1：min；-1：max
        Dim = 3                             # 初始化Dim（决策变量维数）----- 有几个未知量 x1,x2,x3: 3
        varTypes = [0] * Dim                # 初始化决策变量类型，0：连续；1：离散 ----- 未知量都是连续的还是离散的
        lb = [0,0,0]                        # 决策变量下界 ----- x1,x2,x3下界
        ub = [1,1,2]                        # 决策变量上界 ----- x1,x2,x3上界
        # lbin = [1,1,0]                      # 决策变量下边界
        # ubin = [1,1,0]                      # 决策变量上边界 # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub)
        # ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):                 # 目标函数，pop为传入的种群对象
        Vars = pop.Phen                     # 得到决策变量矩阵
        x1 = Vars[:, [0]]                   # 取出第一列得到所有个体的x1组成的列向量
        x2 = Vars[:, [1]]                   # 取出第二列得到所有个体的x2组成的列向量
        x3 = Vars[:, [2]]                   # 取出第三列得到所有个体的x3组成的列向量
        # 计算目标函数值，赋值给pop种群对象的ObjV属性
        pop.ObjV = 4*x1 + 2*x2 + x3 # 目标函数
        # 采用可行性法则处理约束，生成种群个体违反约束程度矩阵
        pop.CV = np.hstack([2*x1 + x2 - 1, x1 + 2*x3 - 2, np.abs(x1 + x2 + x3 - 1)])   # 第1.2.3个约束条件



"""============================实例化问题对象========================"""
problem = MyProblem()                                   # 实例化问题对象

"""==============================种群设置==========================="""
Encoding = 'RI'                                         # 编码方式
NIND = 50                                               # 种群规模
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)                                        # 创建区域描述器
population = ea.Population(Encoding, Field, NIND)       # 实例化种群对象（此时种群还没被真正初始化，仅仅是生成一个种群对象）

"""===========================算法参数设置=========================="""
myAlgorithm = ea.soea_DE_best_1_L_templet(problem, population)      # 实例化一个算法模板对象
myAlgorithm.MAXGEN = 1000                                            # 最大遗传代数
myAlgorithm.mutOper.F = 0.5                                         # 设置差分进化的变异缩放因子，变异概率
myAlgorithm.recOper.XOVR = 0.5                                      # 设置交叉概率
myAlgorithm.drawing = 1                                             # 设置绘图方式

"""=====================调用算法模板进行种群进化====================="""
[population, obj_trace, var_trace] = myAlgorithm.run()              # 执行算法模板 # 输出结果
best_gen = np.argmax(obj_trace[:, 1])                               # 记录最优种群是在哪一代
best_ObjV = obj_trace[best_gen, 1]
print('最优的目标函数值为：%s'%(best_ObjV))
print('最优的决策变量值为：')
for i in range(var_trace.shape[1]):
    print(var_trace[best_gen, i])
print('有效进化代数：%s'%(obj_trace.shape[0]))
print('最优的一代是第 %s 代'%(best_gen + 1))
print('评价次数：%s'%(myAlgorithm.evalsNum))
print('时间已过 %s 秒'%(myAlgorithm.passTime))

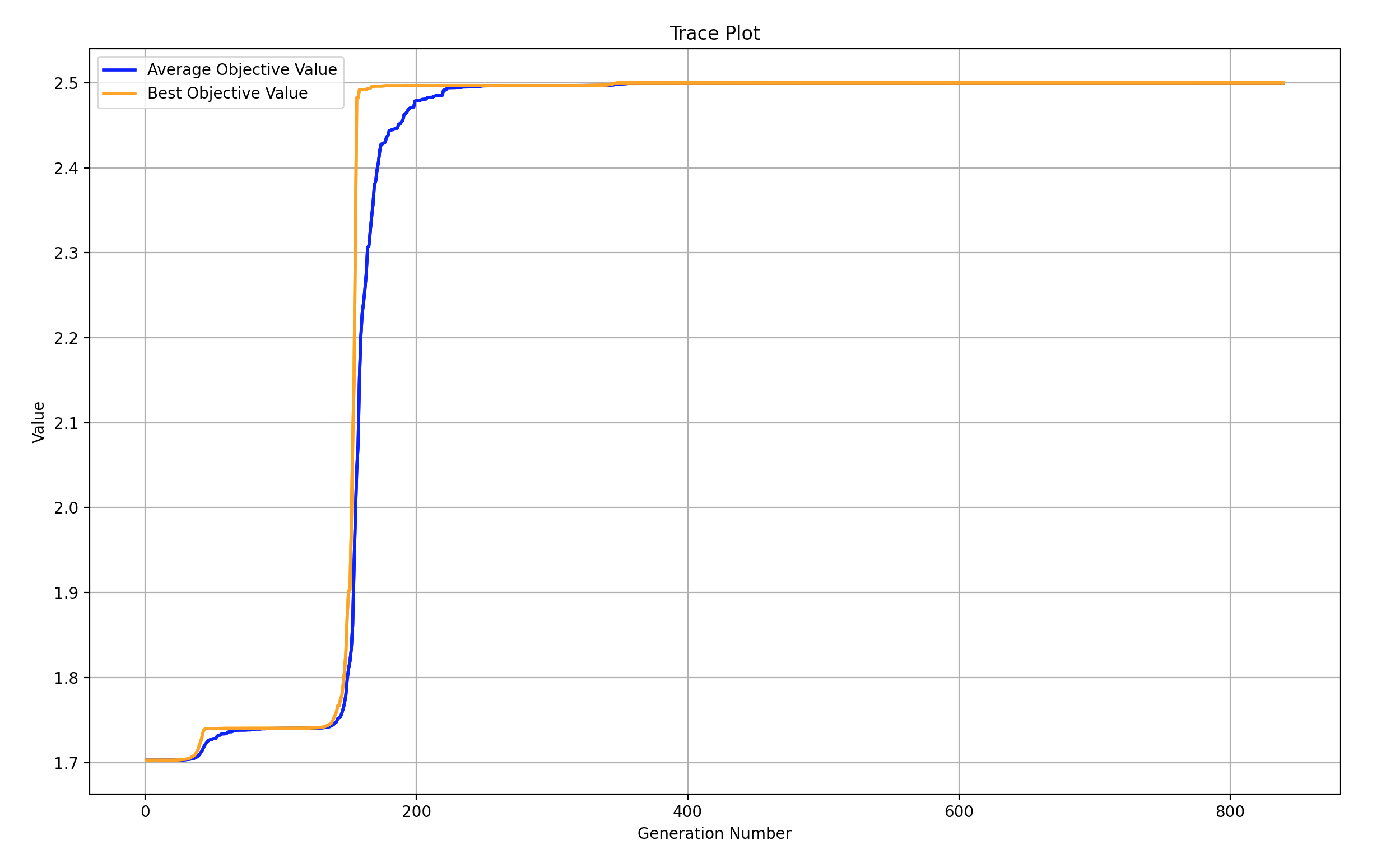
在这里插入图片描述

import numpy as np
import geatpy as ea


# from myaim import MyProblem

class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）----- 有几个目标函数
        maxormins = [1]  # 初始化目标最小最大化标记列表，1：min；-1：max
        Dim = 30  # 初始化Dim（决策变量维数）----- 有几个未知量 x1,x2,x3: 3
        varTypes = [0] * Dim  # 初始化决策变量类型，0：连续；1：离散 ----- 未知量都是连续的还是离散的
        # lb = [0,0,0]                        # 决策变量下界 ----- x1,x2,x3下界
        # ub = [1,1,2]                        # 决策变量上界 ----- x1,x2,x3上界
        lb = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
        ub = [3147, 30977, 1724, 966, 971, 7661, 9385, 2521, 699, 36972, 7885, 10207, 1181, 9768, 8181, 1014, 21293,
              2081, 2816, 21267, 1788, 736, 922, 595, 15114, 23695, 5398, 342, 2005, 381]
        # lbin = [1,1,0]                      # 决策变量下边界
        # ubin = [1,1,0]                      # 决策变量上边界 # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub)
        # ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数，pop为传入的种群对象
        Vars = pop.Phen  # 得到决策变量矩阵
        x1 = Vars[:, [0]]  # 取出第一列得到所有个体的x1组成的列向量
        x2 = Vars[:, [1]]  # 取出第二列得到所有个体的x2组成的列向量
        x3 = Vars[:, [2]]  # 取出第三列得到所有个体的x3组成的列向量
        x4 = Vars[:, [3]]
        x5 = Vars[:, [4]]
        x6 = Vars[:, [5]]
        x7 = Vars[:, [6]]
        x8 = Vars[:, [7]]
        x9 = Vars[:, [8]]
        x10 = Vars[:, [9]]
        x11 = Vars[:, [10]]
        x12 = Vars[:, [11]]
        x13 = Vars[:, [12]]
        x14 = Vars[:, [13]]
        x15 = Vars[:, [14]]
        x16 = Vars[:, [15]]
        x17 = Vars[:, [16]]
        x18 = Vars[:, [17]]
        x19 = Vars[:, [18]]
        x20 = Vars[:, [19]]
        x21 = Vars[:, [20]]  # 取出第一列得到所有个体的x1组成的列向量
        x22 = Vars[:, [21]]  # 取出第二列得到所有个体的x2组成的列向量
        x23 = Vars[:, [22]]  # 取出第三列得到所有个体的x3组成的列向量
        x24 = Vars[:, [23]]
        x25 = Vars[:, [24]]
        x26 = Vars[:, [25]]
        x27 = Vars[:, [26]]
        x28 = Vars[:, [27]]
        x29 = Vars[:, [28]]
        x30 = Vars[:, [29]]
        # 计算目标函数值，赋值给pop种群对象的ObjV属性
        pop.ObjV = 1.2 * (x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10) + \
                   1.1 * (x11 + x12 + x13 + x14 + x15 + x16 + x17 + x18) + \
                   (x19 + x20 + x21 + x22 + x23 + x24 + x25 + x26 + x27 + x28 + x29 + x30)  # 目标函数
        # 采用可行性法则处理约束，生成种群个体违反约束程度矩阵
        pop.CV = np.hstack([56400-((x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10) / 0.6 +
            (x11 + x12 + x13 + x14 + x15 + x16 + x17 + x18) / 0.66 +
                            (x19 + x20 + x21 + x22 + x23 + x24 + x25 + x26 + x27 + x28 + x29 + x30) / 0.72), 4642-(x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10),23833-(x11 + x12 + x13 + x14 + x15 + x16 + x17 + x18),8155-(x19 + x20 + x21 + x22 + x23 + x24 + x25 + x26 + x27 + x28 + x29 + x30)])  # 第1.2.3个约束条件


"""============================实例化问题对象========================"""
problem = MyProblem()  # 实例化问题对象

"""==============================种群设置==========================="""
Encoding = 'RI'  # 编码方式
NIND = 100  # 种群规模
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象（此时种群还没被真正初始化，仅仅是生成一个种群对象）

"""===========================算法参数设置=========================="""
myAlgorithm = ea.soea_DE_best_1_L_templet(problem, population)  # 实例化一个算法模板对象
myAlgorithm.MAXGEN = 1000  # 最大遗传代数
myAlgorithm.mutOper.F = 0.5  # 设置差分进化的变异缩放因子，变异概率
myAlgorithm.recOper.XOVR = 0.5  # 设置交叉概率
myAlgorithm.drawing = 1  # 设置绘图方式

"""=====================调用算法模板进行种群进化====================="""
[population, obj_trace, var_trace] = myAlgorithm.run()  # 执行算法模板 # 输出结果
best_gen = np.argmax(obj_trace[:, 1])  # 记录最优种群是在哪一代
best_ObjV = obj_trace[best_gen, 1]
print('最优的目标函数值为：%s' % (best_ObjV))
print('最优的决策变量值为：')
for i in range(var_trace.shape[1]):
    print(var_trace[best_gen, i])
print('有效进化代数：%s' % (obj_trace.shape[0]))
print('最优的一代是第 %s 代' % (best_gen + 1))
print('评价次数：%s' % (myAlgorithm.evalsNum))
print('时间已过 %s 秒' % (myAlgorithm.passTime))

在这里插入图片描述

5 多目标函数 - 带约束

import numpy as np
import geatpy as ea  # import geatpy


# from MyProblem import MyProblem     # 导入自定义问题接口

class MyProblem(ea.Problem):  # 继承Problem父类

    def __init__(self):
        name = 'BNH'  # 初始化name（函数名称，可以随意设置）
        M = 2  # 初始化M（目标维数）
        maxormins = [1] * M  # 初始化maxormins
        Dim = 2  # 初始化Dim（决策变量维数）
        varTypes = [0] * Dim  # 初始化varTypes（决策变量的类型，0：实数；1：整数）
        lb = [0] * Dim  # 决策变量下界
        ub = [5, 3]  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界
        ubin = [1] * Dim  # 决策变量上边界
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        Vars = pop.Phen  # 得到决策变量矩阵
        x1 = Vars[:, [0]]
        x2 = Vars[:, [1]]
        f1 = 4 * x1 ** 2 + 4 * x2 ** 2
        f2 = (x1 - 5) ** 2 + (x2 - 5) ** 2
        # 采用可行性法则处理约束
        pop.CV = np.hstack([(x1 - 5) ** 2 + x2 ** 2 - 25, -(x1 - 8) ** 2 - (x2 - 3) ** 2 + 7.7])
        # 把求得的目标函数值赋值给种群pop的ObjV
        pop.ObjV = np.hstack([f1, f2])

    def calBest(self):  # 计算全局最优解
        N = 10000  # 欲得到10000个真实前沿点
        x1 = np.linspace(0, 5, N)
        x2 = x1.copy()
        x2[x1 >= 3] = 3
        return np.vstack((4 * x1 ** 2 + 4 * x2 ** 2, (x1 - 5) ** 2 + (x2 - 5) ** 2)).T


"""=========================实例化问题对象==========================="""
problem = MyProblem()  # 实例化问题对象

"""===========================种群设置=============================="""
Encoding = 'RI'  # 编码方式
NIND = 100  # 种群规模
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象（此时种群还没被真正初始化，仅仅是生成一个种群对象）

"""=========================算法参数设置============================"""
myAlgorithm = ea.moea_NSGA2_templet(problem, population)  # 实例化一个算法模板对象
myAlgorithm.MAXGEN = 200  # 最大遗传代数
myAlgorithm.drawing = 1  # 设置绘图方式

"""===================调用算法模板进行种群进化=======================
调用run执行算法模板，得到帕累托最优解集NDSet。
NDSet是一个种群类Population的对象。
NDSet.ObjV为最优解个体的目标函数值；NDSet.Phen为对应的决策变量值。
详见Population.py中关于种群类的定义。
"""
NDSet = myAlgorithm.run()  # 执行算法模板，得到非支配种群
NDSet.save()  # 把结果保存到文件中 # 输出
print('用时：%f 秒' % (myAlgorithm.passTime))
print('评价次数：%d 次' % (myAlgorithm.evalsNum))
print('非支配个体数：%d 个' % (NDSet.sizes))
print('单位时间找到帕累托前沿点个数：%d 个' % (int(NDSet.sizes // myAlgorithm.passTime)))
# 计算指标
PF = problem.getBest()  # 获取真实前沿
if PF is not None and NDSet.sizes != 0:
    GD = ea.indicator.GD(NDSet.ObjV, PF)  # 计算GD指标 - 世代距离
    IGD = ea.indicator.IGD(NDSet.ObjV, PF)  # 计算IGD指标 - 反转世代距离
    HV = ea.indicator.HV(NDSet.ObjV, PF)  # 计算HV指标 - 超体积
    Spacing = ea.indicator.Spacing(NDSet.ObjV)  # 计算Spacing指标 - 广泛性评价
    print('GD: %f' % GD)
    print('IGD: %f' % IGD)
    print('HV: %f' % HV)
    print('Spacing: %f' % Spacing)

"""=====================进化过程指标追踪分析========================"""
if PF is not None:
    metricName = [['IGD'], ['HV']]
    [NDSet_trace, Metrics] = ea.indicator.moea_tracking(myAlgorithm.pop_trace, PF, metricName, problem.maxormins)
    # 绘制指标追踪分析图
    ea.trcplot(Metrics, labels=metricName, titles=metricName)

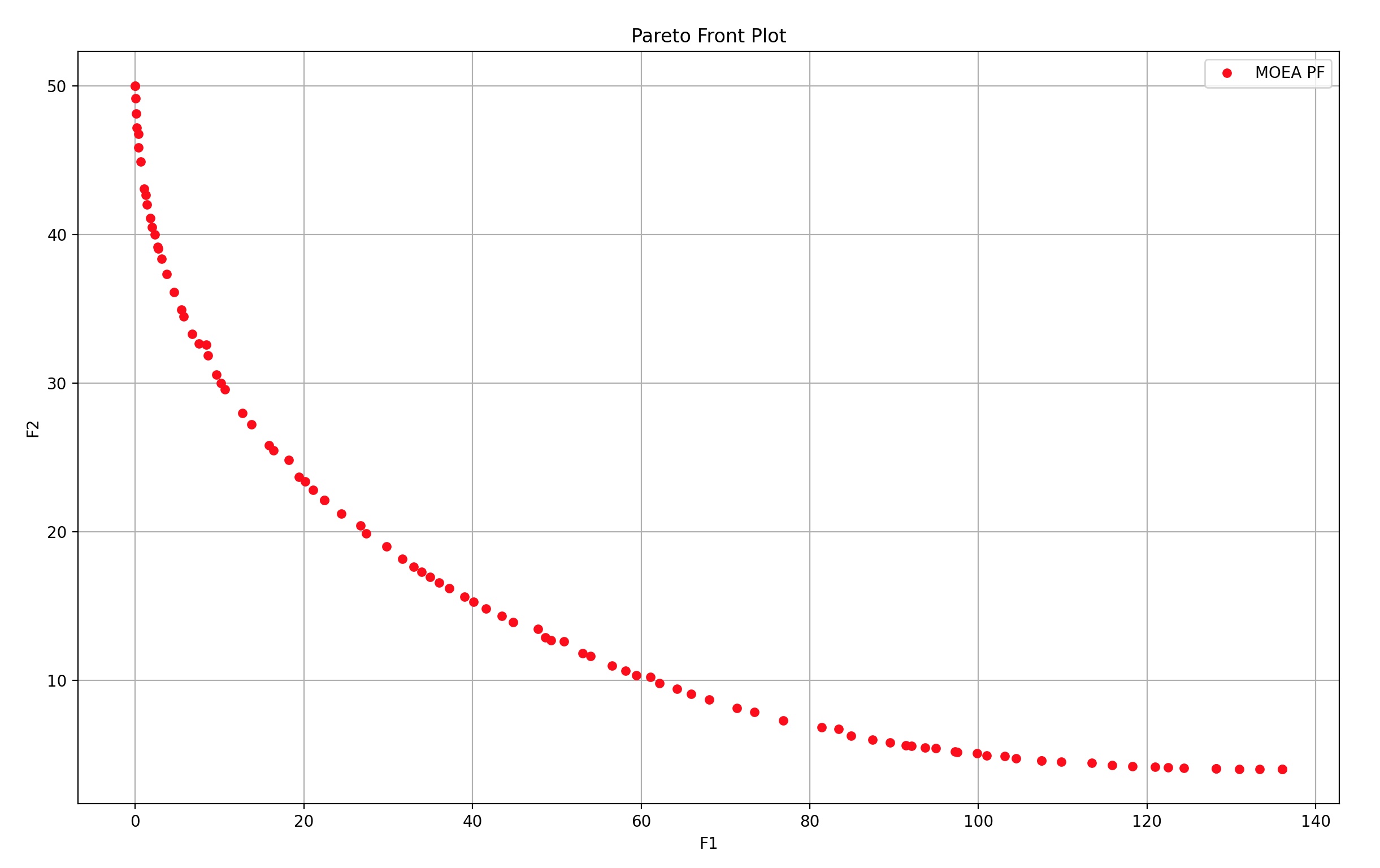
在这里插入图片描述

6 单目标多变量函数 - 带约束,但有最优目标函数值和最优控制变量值

import numpy as np
"""main_solve.py"""
import geatpy as ea # import geatpy


class MyProblem(ea.Problem): # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）

        M = 1  # 初始化M（目标维数）
        maxormins = [-1]  # 初始化目标最小最大化标记列表，1：min；-1：max
        Dim = 3  # 初始化Dim（决策变量维数）
        varTypes = [0] * Dim  # 初始化决策变量类型，0：连续；1：离散
        lb = [0, 0, 0]  # 决策变量下界
        ub = [1, 1, 2]  # 决策变量上界
        lbin = [1, 1, 0]  # 决策变量下边界
        ubin = [1, 1, 0]  # 决策变量上边界
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb,
                        ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数，pop为传入的种群对象
        Vars = pop.Phen  # 得到决策变量矩阵

        x1 = Vars[:, [0]]  # 取出第一列得到所有个体的x1组成的列向量
        x2 = Vars[:, [1]]  # 取出第二列得到所有个体的x2组成的列向量
        x3 = Vars[:, [2]]  # 取出第三列得到所有个体的x3组成的列向量 # 计算目标函数值，赋值给pop种群对象的ObjV属性
        pop.ObjV = 4 * x1 + 2 * x2 + x3
        # 采用可行性法则处理约束，生成种群个体违反约束程度矩阵
        pop.CV = np.hstack([2 * x1 + x2 - 1,  # 第一个约束
                        x1 + 2 * x3 - 2,  # 第二个约束
                        np.abs(x1 + x2 + x3 - 1)])  # 第三个约束


# from myaim import MyProblem # 导入自定义问题接口
"""============================实例化问题对象========================"""
problem = MyProblem() # 实例化问题对象
"""==============================种群设置==========================="""
Encoding = 'RI' # 编码方式
NIND = 50 # 种群规模
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges,problem.borders) # 创建区域描述器
population = ea.Population(Encoding, Field, NIND) # 实例化种群对象（此时种群还没被真正初始化，仅仅是生成一个种群对象）
"""===========================算法参数设置=========================="""
myAlgorithm = ea.soea_DE_best_1_L_templet(problem, population) # 实例化一个算法模板对象
myAlgorithm.MAXGEN = 1000 # 最大进化代数
myAlgorithm.mutOper.F = 0.5 # 差分进化中的参数F
myAlgorithm.recOper.XOVR = 0.7 # 设置交叉概率
myAlgorithm.logTras = 1 # 设置每隔多少代记录日志，若设置成0则表示不记录日志
myAlgorithm.verbose = True # 设置是否打印输出日志信息
myAlgorithm.drawing = 1 # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
"""==========================调用算法模板进行种群进化==============="""
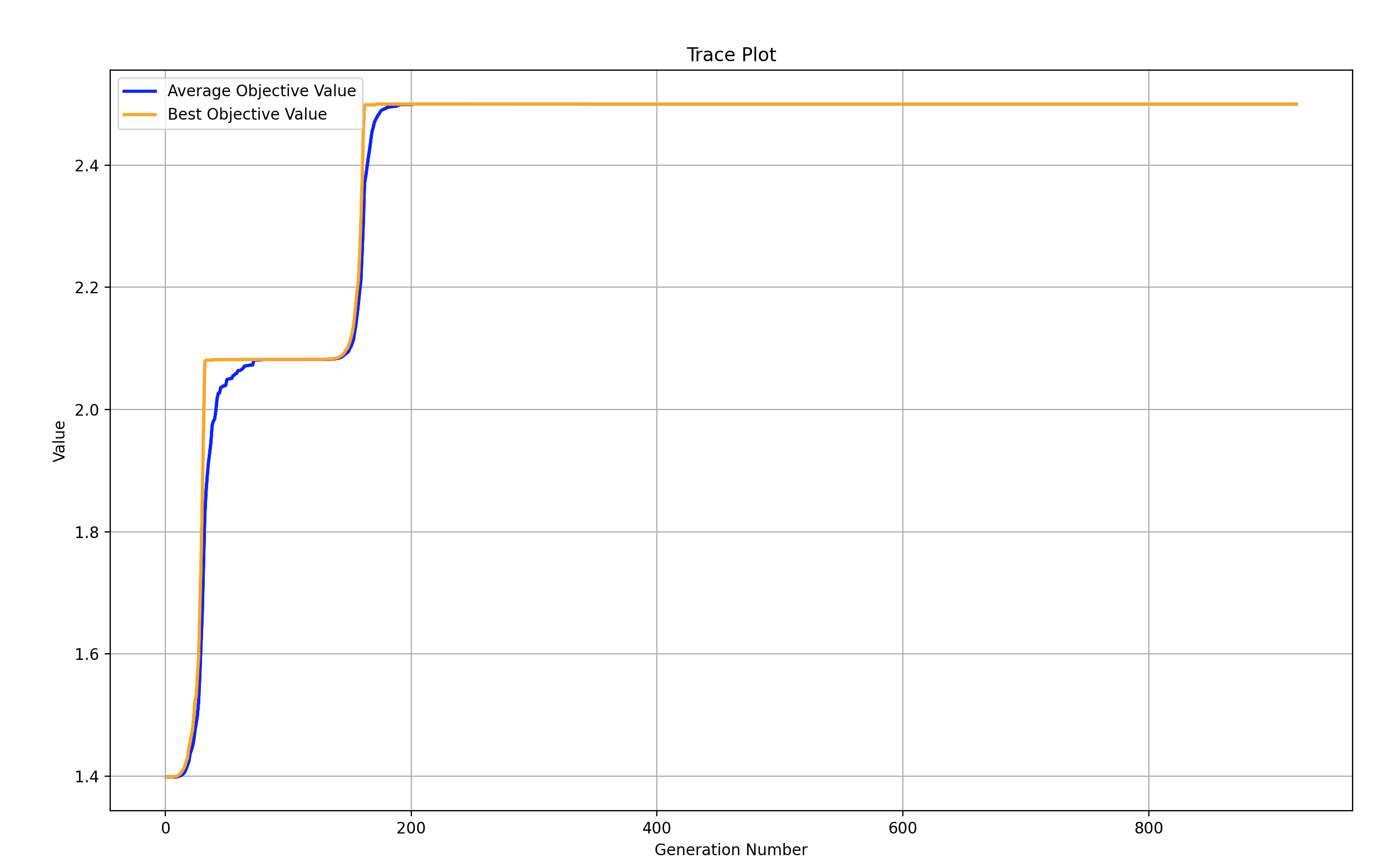
[BestIndi, population] = myAlgorithm.run() # 执行算法模板，得到最优个体以及最后一代种群
BestIndi.save() # 把最优个体的信息保存到文件中
"""=================================输出结果======================="""
print('评价次数：%s' % myAlgorithm.evalsNum)
print('时间花费 %s 秒' % myAlgorithm.passTime)
if BestIndi.sizes != 0:
    print('最优的目标函数值为：%s' % BestIndi.ObjV[0][0])
    print('最优的控制变量值为：')
    for i in range(BestIndi.Phen.shape[1]):
        print(BestIndi.Phen[0, i])
else:
    print('此次未找到可行解。')

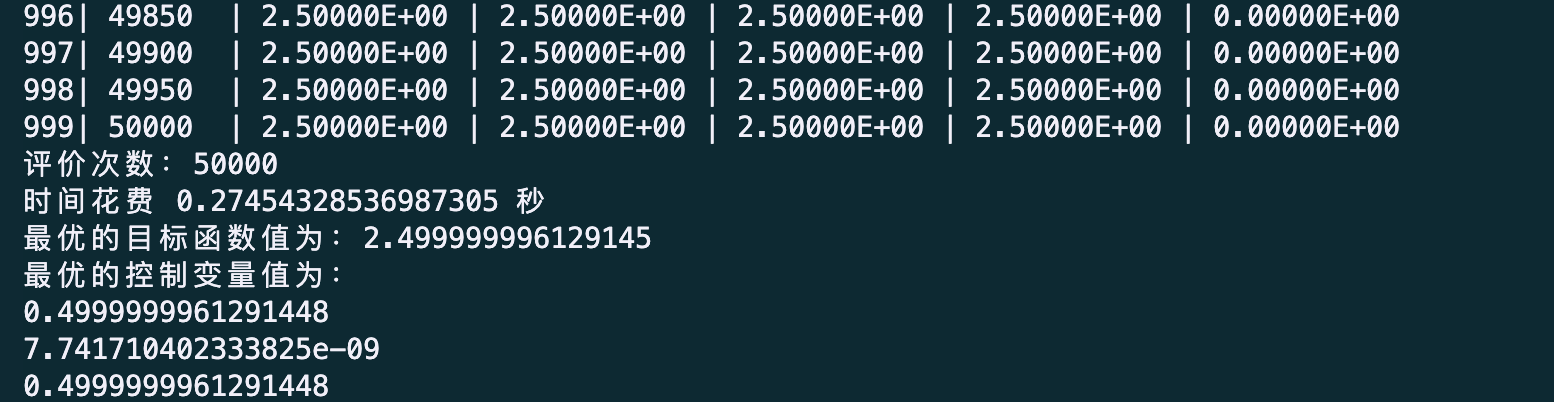
在这里插入图片描述

30个x

import numpy as np

"""main_solve.py"""
import geatpy as ea  # import geatpy


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）

        M = 1  # 初始化M（目标维数）
        maxormins = [1]  # 初始化目标最小最大化标记列表，1：min；-1：max
        Dim = 30  # 初始化Dim（决策变量维数）
        varTypes = [0] * Dim  # 初始化决策变量类型，0：连续；1：离散
        # lb = [0, 0, 0]  # 决策变量下界
        # ub = [1, 1, 2]  # 决策变量上界
        lb = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
        ub = [3147, 30977, 1724, 966, 971, 7661, 9385, 2521, 699, 36972, 7885, 10207, 1181, 9768, 8181, 1014, 21293,
              2081, 2816, 21267, 1788, 736, 922, 595, 15114, 23695, 5398, 342, 2005, 381]

        lbin = [1]*Dim  # 决策变量下边界
        ubin = [1]*Dim  # 决策变量上边界
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb,
                            ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数，pop为传入的种群对象
        Vars = pop.Phen  # 得到决策变量矩阵

        x1 = Vars[:, [0]]  # 取出第一列得到所有个体的x1组成的列向量
        x2 = Vars[:, [1]]  # 取出第二列得到所有个体的x2组成的列向量
        x3 = Vars[:, [2]]  # 取出第三列得到所有个体的x3组成的列向量
        x4 = Vars[:, [3]]
        x5 = Vars[:, [4]]
        x6 = Vars[:, [5]]
        x7 = Vars[:, [6]]
        x8 = Vars[:, [7]]
        x9 = Vars[:, [8]]
        x10 = Vars[:, [9]]
        x11 = Vars[:, [10]]
        x12 = Vars[:, [11]]
        x13 = Vars[:, [12]]
        x14 = Vars[:, [13]]
        x15 = Vars[:, [14]]
        x16 = Vars[:, [15]]
        x17 = Vars[:, [16]]
        x18 = Vars[:, [17]]
        x19 = Vars[:, [18]]
        x20 = Vars[:, [19]]
        x21 = Vars[:, [20]]  # 取出第一列得到所有个体的x1组成的列向量
        x22 = Vars[:, [21]]  # 取出第二列得到所有个体的x2组成的列向量
        x23 = Vars[:, [22]]  # 取出第三列得到所有个体的x3组成的列向量
        x24 = Vars[:, [23]]
        x25 = Vars[:, [24]]
        x26 = Vars[:, [25]]
        x27 = Vars[:, [26]]
        x28 = Vars[:, [27]]
        x29 = Vars[:, [28]]
        x30 = Vars[:, [29]]
        # 计算目标函数值，赋值给pop种群对象的ObjV属性
        pop.ObjV = 1.2 * (x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10) + \
                   1.1 * (x11 + x12 + x13 + x14 + x15 + x16 + x17 + x18) + \
                   (x19 + x20 + x21 + x22 + x23 + x24 + x25 + x26 + x27 + x28 + x29 + x30)  # 目标函数

        # 采用可行性法则处理约束，生成种群个体违反约束程度矩阵
        pop.CV = np.hstack([56400 - ((x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10) / 0.6 +
                                     (x11 + x12 + x13 + x14 + x15 + x16 + x17 + x18) / 0.66 +
                                     (x19 + x20 + x21 + x22 + x23 + x24 + x25 + x26 + x27 + x28 + x29 + x30) / 0.72),
                            4642 - (x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10),
                            23833 - (x11 + x12 + x13 + x14 + x15 + x16 + x17 + x18), 8155 - (
                                        x19 + x20 + x21 + x22 + x23 + x24 + x25 + x26 + x27 + x28 + x29 + x30)])  # 第1.2.3个约束条件



# from myaim import MyProblem # 导入自定义问题接口
"""============================实例化问题对象========================"""
problem = MyProblem()  # 实例化问题对象
"""==============================种群设置==========================="""
Encoding = 'RI'  # 编码方式
NIND = 100  # 种群规模
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象（此时种群还没被真正初始化，仅仅是生成一个种群对象）
"""===========================算法参数设置=========================="""
myAlgorithm = ea.soea_DE_best_1_L_templet(problem, population)  # 实例化一个算法模板对象
myAlgorithm.MAXGEN = 1000  # 最大进化代数
myAlgorithm.mutOper.F = 0.5  # 差分进化中的参数F
myAlgorithm.recOper.XOVR = 0.7  # 设置交叉概率
myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
myAlgorithm.verbose = True  # 设置是否打印输出日志信息
myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
"""==========================调用算法模板进行种群进化==============="""
[BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
BestIndi.save()  # 把最优个体的信息保存到文件中
"""=================================输出结果======================="""
print('评价次数：%s' % myAlgorithm.evalsNum)
print('时间花费 %s 秒' % myAlgorithm.passTime)
if BestIndi.sizes != 0:
    print('最优的目标函数值为：%s' % BestIndi.ObjV[0][0])
    print('最优的控制变量值为：')
    for i in range(BestIndi.Phen.shape[1]):
        print(BestIndi.Phen[0, i])
else:
    print('此次未找到可行解。')

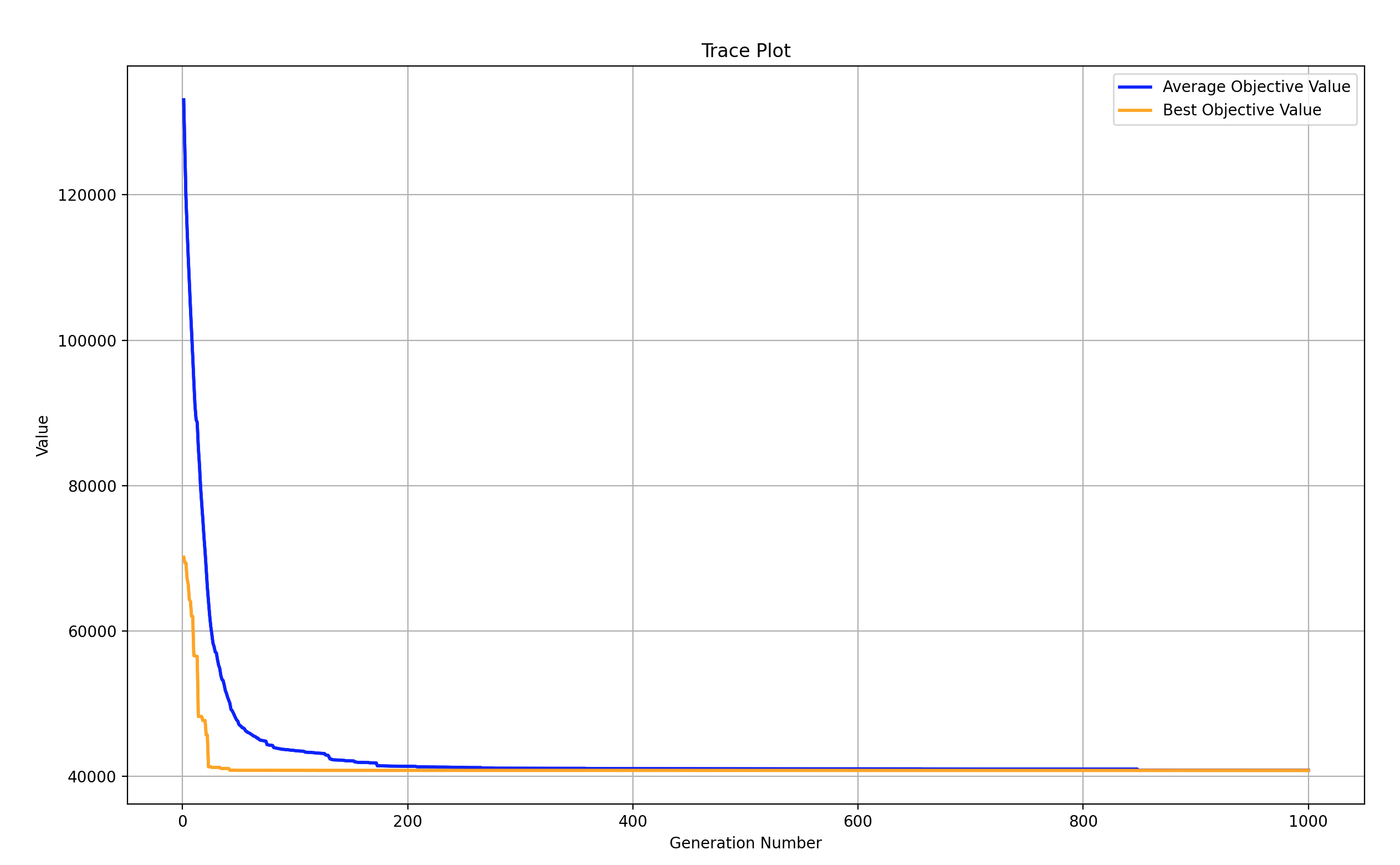
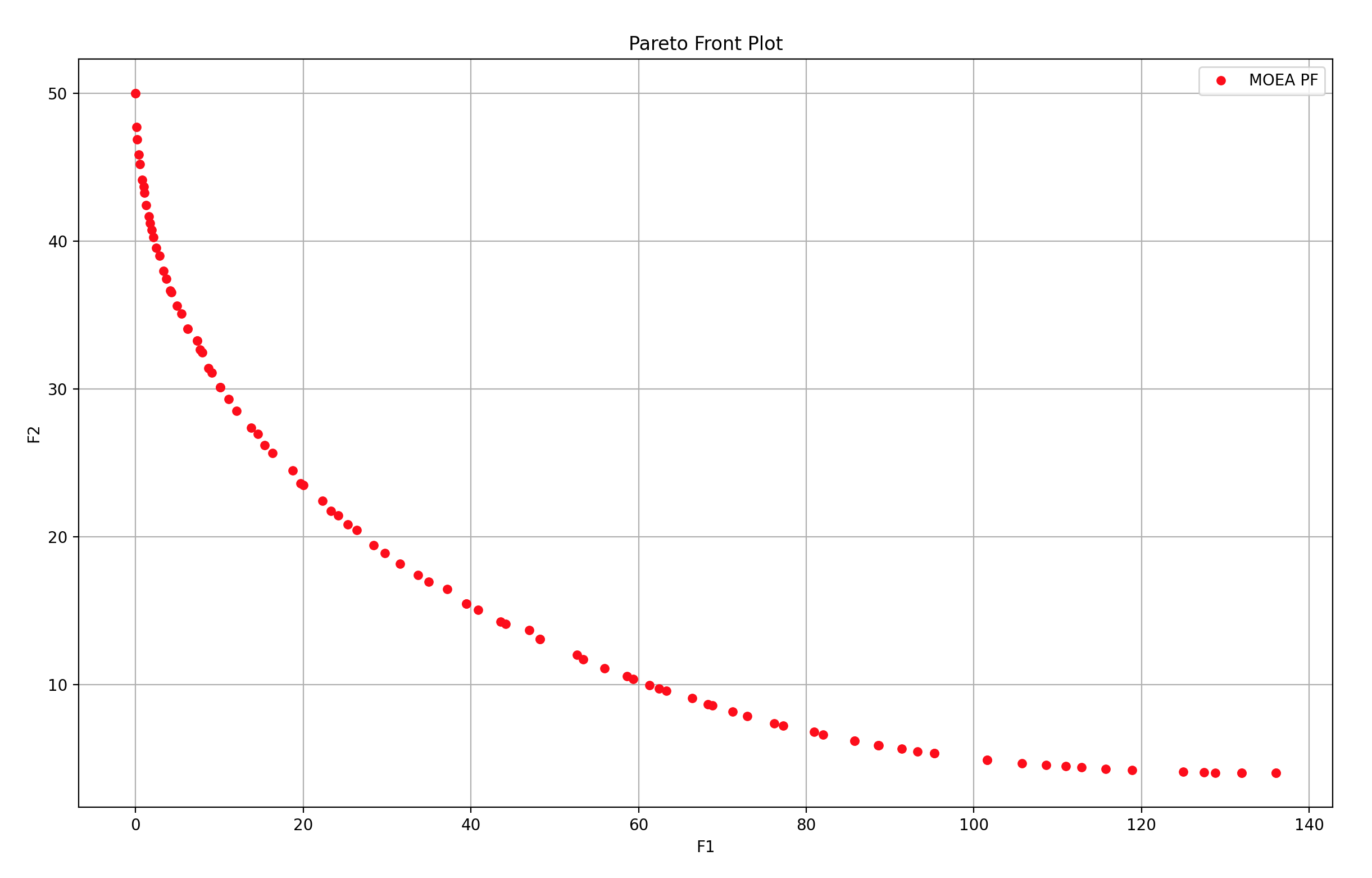
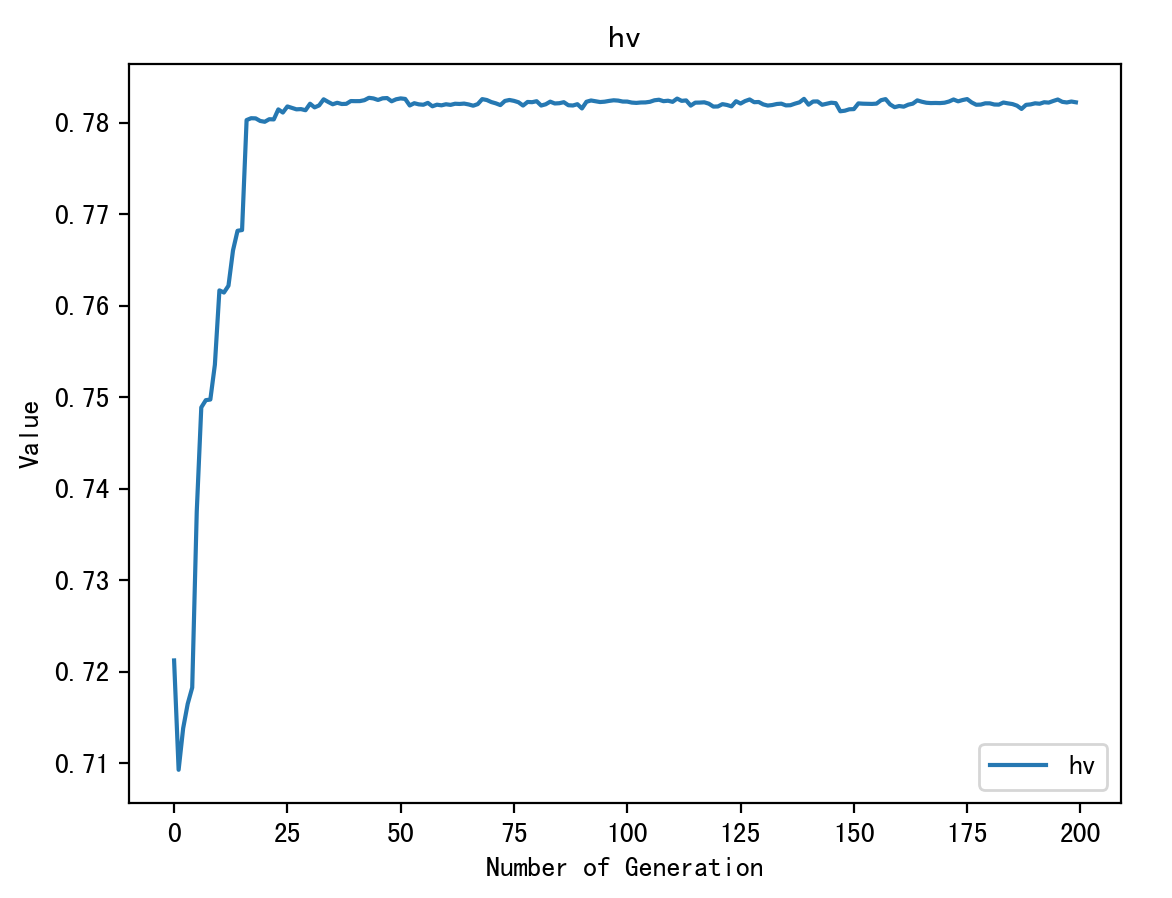
在这里插入图片描述

7 多目标函数 - 带约束，多了HV趋势图和IGD趋势图

import numpy as np
import geatpy as ea # import geatpy
# from ga_more_aim import MyProblem # 导入自定义问题接口


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'BNH'  # 初始化name（函数名称，可以随意设置）
        M = 2  # 初始化M（目标维数）
        maxormins = [1] * M  # 初始化maxormins
        Dim = 2  # 初始化Dim（决策变量维数）
        varTypes = [0] * Dim  # 初始化varTypes（决策变量的类型，0：实数；1：整数）
        lb = [0] * Dim  # 决策变量下界
        ub = [5, 3]  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界
        ubin = [1] * Dim  # 决策变量上边界 # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        Vars = pop.Phen  # 得到决策变量矩阵
        x1 = Vars[:, [0]]  # 注意这样得到的x1是一个列向量，表示所有个体的x1
        x2 = Vars[:, [1]]
        f1 = 4 * x1 ** 2 + 4 * x2 ** 2
        f2 = (x1 - 5) ** 2 + (x2 - 5) ** 2
        # 采用可行性法则处理约束
        pop.CV = np.hstack([(x1 - 5) ** 2 + x2 ** 2 - 25, -(x1 - 8) ** 2 - (x2 - 3) ** 2 + 7.7])
        # 把求得的目标函数值赋值给种群pop的ObjV
        pop.ObjV = np.hstack([f1, f2])

    ## 目标函数主要需要计算出CV和ObjV



"""=======================实例化问题对象==========================="""
problem = MyProblem() # 实例化问题对象
"""=========================种群设置=============================="""
Encoding = 'RI' # 编码方式
NIND = 100 # 种群规模
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges,problem.borders) # 创建区域描述器
population = ea.Population(Encoding, Field, NIND) # 实例化种群对象（此时种群还没被真正初始化，仅仅是生成一个种群对象）
"""=========================算法参数设置============================"""
myAlgorithm = ea.moea_NSGA2_templet(problem, population) # 实例化一个算法模板对象
myAlgorithm.mutOper.Pm = 0.2 # 修改变异算子的变异概率
myAlgorithm.recOper.XOVR = 0.9 # 修改交叉算子的交叉概率
myAlgorithm.MAXGEN = 200 # 最大进化代数
myAlgorithm.logTras = 1 # 设置每多少代记录日志，若设置成0则表示不记录日志
myAlgorithm.verbose = False # 设置是否打印输出日志信息
myAlgorithm.drawing = 1 # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
"""==========================调用算法模板进行种群进化==============
调用run执行算法模板，得到帕累托最优解集NDSet以及最后一代种群。
NDSet是一个种群类Population的对象。
NDSet.ObjV为最优解个体的目标函数值；NDSet.Phen为对应的决策变量值。
详见Population.py中关于种群类的定义。
"""
[NDSet, population] = myAlgorithm.run() # 执行算法模板，得到非支配种群以及最后一代种群
NDSet.save() # 把非支配种群的信息保存到文件中
"""===========================输出结果========================"""
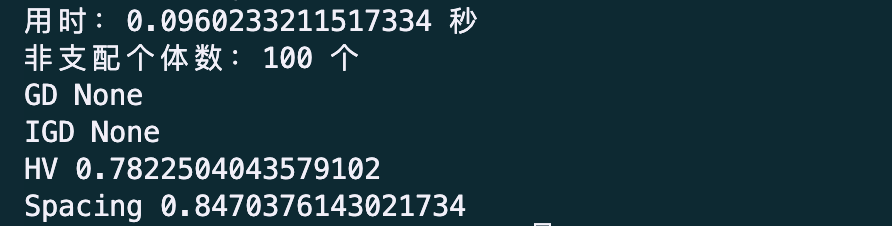
print('用时：%s 秒' % myAlgorithm.passTime)
print('非支配个体数：%d 个' % NDSet.sizes) if NDSet.sizes != 0 else print('没有找到可行解！')
if myAlgorithm.log is not None and NDSet.sizes != 0:
    print('GD', myAlgorithm.log['gd'][-1])
    print('IGD', myAlgorithm.log['igd'][-1])
    print('HV', myAlgorithm.log['hv'][-1])
    print('Spacing', myAlgorithm.log['spacing'][-1])
"""======================进化过程指标追踪分析=================="""
metricName = [['igd'], ['hv']]
Metrics = np.array([myAlgorithm.log[metricName[i][0]] for i in range(len(metricName))]).T
# 绘制指标追踪分析图
ea.trcplot(Metrics, labels=metricName, titles=metricName)