一. BFS的简单介绍
深度优先搜索DFS和广度优先搜索BFS是经常使用的搜索算法,在各类题目中都有广泛的应用。
深度优先搜索算法(英语:Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次。
广度优先搜索算法(Breadth-First Search,缩写为 BFS),又称为宽度优先搜索,是一种图形搜索算法。简单的说,BFS 是从根结点开始,沿着树的宽度遍历树的结点。如果所有结点均被访问,则算法中止。
一般来说,能用DFS的,一般都可以用BFS解决,反过来同理。但是不同的题目,对于DFS和BFS的复杂度可能是有些差别的,对于有些题目,用BFS更容易解决,会有更少的时间复杂度。
二. BFS模板
BFS的载体一般选择双端队列,两边都可以增删,可以满足一些特殊的情况,比如0-1BFS(Ref.[1]).
一般在循环体内都有另一层循环,此层循环是同层循环,一般在同层循环中,答案的更新是一样的,可以理解为树的同一层,具有同样的深度。
class Solution {
public BFS(TreeNode root) {
//双端队列,用来存储元素
Deque<TreeNode> queue = new ArrayDeque<>();
//添加首个元素
queue.add(首个元素);
//当队列不为空一直进行循环,直到队列不再有元素
while(!queue.isEmpty()){
int n = queue.size();
//得到队列的大小
for(int i = 0; i < n; i++){
var t = queue.poll();
在同一层的操作;
...
}
在非同层更新答案;
}
返回答案;
}
}
三. 典型案例
1.leetcode102 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]] 
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ans = new ArrayList<>();
Deque<TreeNode> queue = new ArrayDeque<>();
if(root != null){
queue.add(root);
}
while(!queue.isEmpty()){
List<Integer> list = new ArrayList<>();
int n = queue.size();
for(int i = 0; i < n; i++){
TreeNode node = queue.poll();
list.add(node.val);
if(node.left != null){
queue.add(node.left);
}
if(node.right != null){
queue.add(node.right);
}
}
ans.add(list);
}
return ans;
}
}本题小结:(1)此题是BFS的典型题目, 在同层添加左右子节点,同层节点具有相同的深度
(2)以颜色来区分同层,可以得到表示更为清晰的二叉树的层序遍历:

那么,原本的二叉树被分为三层,第一层{3},第二层{9,20},第三层{15,17},同一层内的操作在for循环中完成
2.leetcode 1091 二进制矩阵中的最短路径
给你一个 n x n 的二进制矩阵 grid 中,返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径,返回 -1 。
二进制矩阵中的 畅通路径 是一条从 左上角 单元格(即,(0, 0))到 右下角 单元格(即,(n - 1, n - 1))的路径,该路径同时满足下述要求:
路径途经的所有单元格的值都是 0 。
路径中所有相邻的单元格应当在 8 个方向之一 上连通(即,相邻两单元之间彼此不同且共享一条边或者一个角)。
畅通路径的长度 是该路径途经的单元格总数。
输入:grid = [[0,1],[1,0]]
输出:2 
class Solution {
public int shortestPathBinaryMatrix(int[][] grid) {
if(grid[0][0] == 1) return -1;
Deque<Integer> q = new LinkedList<>();
int m = grid.length;
int n = grid[0].length;
boolean[] vis = new boolean[m*n];
q.addLast(0);
vis[0] = true;
int ans = 0;
while(!q.isEmpty()){
int size = q.size();
for(int k = 0; k < size; k++){
int t = q.pollFirst();
if(t == m*n-1) return ans+1;
int x = t/n;
int y = t%n;
for(int i = -1; i <= 1; i++){
for(int j = -1; j <=1; j++){
int xx = x+i;
int yy = y+j;
if(xx >= m || yy >= n || xx < 0 || yy < 0 || grid[xx][yy] == 1) continue;
if(vis[xx*n+yy]) continue;
q.addLast(xx*n+yy);
vis[xx*n+yy] = true;
}
}
}
ans++;
}
return -1;
}
}本题小结:(1)此题也是BFS的典型题目,此题经典的解法即为BFS或者DFS,类似的还有走迷宫的题目,在矩阵或者图中,从起点到终点的题目几乎都可以用DFS或者BFS来解决。
(2)在同一层具有相同的深度,即在for循环内ans是相同的,在for循环外来更新ans。
(3)来到当前点的下一个点的方向可以朝着上下左右行走,那么原本最初的for循环变为两层,但逻辑都是一样的,即:寻找下一步可以走的所有可能性。
(4)vis[xx*n+yy] = true;走过的进行标记,这在回溯等方法中也经常使用,在DFS、BFS此类暴力搜索的方法中也不不得不用的措施。
3.leetcode 1210 穿过迷宫的最少移动次数
你还记得那条风靡全球的贪吃蛇吗?
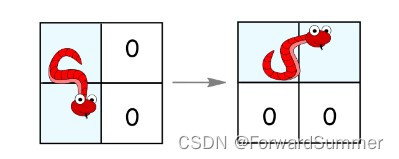
我们在一个 n*n 的网格上构建了新的迷宫地图,蛇的长度为 2,也就是说它会占去两个单元格。蛇会从左上角((0, 0) 和 (0, 1))开始移动。我们用 0 表示空单元格,用 1 表示障碍物。蛇需要移动到迷宫的右下角((n-1, n-2) 和 (n-1, n-1))。
每次移动,蛇可以这样走:
如果没有障碍,则向右移动一个单元格。并仍然保持身体的水平/竖直状态。
如果没有障碍,则向下移动一个单元格。并仍然保持身体的水平/竖直状态。
如果它处于水平状态并且其下面的两个单元都是空的,就顺时针旋转 90 度。蛇从((r, c)、(r, c+1))移动到 ((r, c)、(r+1, c))。

如果它处于竖直状态并且其右面的两个单元都是空的,就逆时针旋转 90 度。蛇从((r, c)、(r+1, c))移动到((r, c)、(r, c+1))。
返回蛇抵达目的地所需的最少移动次数。
如果无法到达目的地,请返回 -1。
输入:grid = [[0,0,0,0,0,1],
[1,1,0,0,1,0],
[0,0,0,0,1,1],
[0,0,1,0,1,0],
[0,1,1,0,0,0],
[0,1,1,0,0,0]]
输出:11
解释:
一种可能的解决方案是 [右, 右, 顺时针旋转, 右, 下, 下, 下, 下, 逆时针旋转, 右, 下]。

class Solution {
int r;
int c;
int[][] grid;
public int minimumMoves(int[][] grid) {
this.grid = grid;
r = grid.length;
c = grid[0].length;
int ans = 0;
int endL = r*c - 2;
int endF = r*c - 1;
Deque<int[]> q = new ArrayDeque<>();
boolean[][] vis = new boolean[r*c][r*c];
// 尾巴 头 别反了
q.add(new int[]{0,1});
vis[0][1] = true;
while(!q.isEmpty()){
for(int k = q.size(); k > 0; k--){
var t = q.pollFirst();
int tF = t[1];
int tL = t[0];
if(tF == endF && tL == endL){
return ans;
}
int tFx = t[1]/c;//头x
int tFy = t[1]%c;//头y
int tLx = t[0]/c;//尾x
int tLy = t[0]%c;//尾y
//水平状态 向右平移一格 (tFx,tFy+1) (tLx,tLy+1)
//垂直状态 向右平移一个 (tFx,tFy+1) (tLx,tLy+1)
if(tFx == tLx){//当前是水平状态
if(tFy+1 < c && grid[tFx][tFy+1] == 0 && !vis[tLx*c+tLy+1][tFx*c+tFy+1]){//水平向右
q.offerLast(new int[]{tLx*c+tLy+1,tFx*c+tFy+1});
vis[tLx*c+tLy+1][tFx*c+tFy+1] = true;
}
if(tFx+1 < r && grid[tFx+1][tFy] == 0 && grid[tLx+1][tLy] == 0){
if(!vis[(tLx+1)*c+tLy][(tFx+1)*c+tFy]){//水平向下
q.offerLast(new int[]{(tLx+1)*c+tLy,(tFx+1)*c+tFy});
vis[(tLx+1)*c+tLy][(tFx+1)*c+tFy] = true;
}
if(!vis[tLx*c+tLy][(tFx+1)*c+tFy-1]){//右旋转
q.offerLast(new int[]{tLx*c+tLy,(tFx+1)*c+tFy-1});
vis[tLx*c+tLy][(tFx+1)*c+tFy-1] = true;
}
}
}
else{//当前是垂直状态
if(tFx+1 < r && grid[tFx+1][tFy] == 0 && !vis[(tLx+1)*c+tLy][(tFx+1)*c+tFy]){//水平向下
q.offerLast(new int[]{(tLx+1)*c+tLy,(tFx+1)*c+tFy});
vis[(tLx+1)*c+tLy][(tFx+1)*c+tFy] = true;
}
if(tFy+1 < c && grid[tFx][tFy+1] == 0 && grid[tLx][tLy+1] == 0){
if(!vis[tLx*c+tLy+1][tFx*c+tFy+1]){//水平向右
q.offerLast(new int[]{tLx*c+tLy+1, tFx*c+tFy+1});
vis[tLx*c+tLy+1][tFx*c+tFy+1] = true;
}
if(!vis[tLx*c+tLy][(tFx-1)*c+tFy+1]){//左旋转
q.offerLast(new int[]{tLx*c+tLy,(tFx-1)*c+tFy+1});
vis[tLx*c+tLy][(tFx-1)*c+tFy+1] = true;
}
}
}
}
ans++;
}
return -1;
}
}本题小结:(1)此题是走迷宫类的题目,和上述题目不同,走的方式有一定的限制,但是总体的额方法是类似的
(2)本解法采用水平,垂直分类处理,会出现较多的if-else,非常不美观,容易出错,但是可以明确大体思路,更简便的做法可参考Ref.[2]
参考来源 Ref.
[1] 灵茶山艾府 还在 if-else?一个循环处理六种移动!(Python/Java/C++/Go)