掌握imgproc组件：opencv-图像轮廓与图像分割修复

news2024/10/4 2:34:24

图像轮廓与图像分割修复

  • 1.查找并绘制轮廓
    • 1.1 寻找轮廓：findContours()函数
    • 1.2 绘制轮廓：drawContours()函数
    • 1.3 案例程序：轮廓查找
  • 2. 寻找物体的凸包
    • 2.1 凸包
    • 2.2 寻找凸包：convexHull()函数
    • 2.3 案例：寻找和绘制物体的凸包
  • 3.使用多边形将轮廓包围
    • 3.1 返回外部矩形边界：boundingRect()函数
    • 3.2 寻找最小包围矩形：minAreaRect()函数
    • 3.3 寻找最小包围圆形：minEnclosingCircle()函数
    • 3.4 用椭圆拟合二维点集：fitEllipse()函数
    • 3.5 逼近多边形曲线：approxPolyDP()函数
    • 3.6 示例程序：创建包围轮廓的矩形边界
  • 4. 图像的矩
    • 4.1 矩的计算：moments()函数
    • 4.2 计算轮廓面积：contourArea()函数
    • 4.3 计算轮廓长度：arcLength()函数
  • 5. 分水岭算法
    • 5.1 实现分水岭算法：watershed()函数
  • 6. 图像修补
    • 6.1 图像修补函数:inpaint()
    • 6.2 图像修补案例

1.查找并绘制轮廓

一个轮廓一般对应一系列的点，也就是图像中的一条曲线。其表示方法可能根据不同的情况而有所不同。在OpenCV中，可以用findContours()函数从二值图像中查找轮廓。

1.1 寻找轮廓：findContours()函数

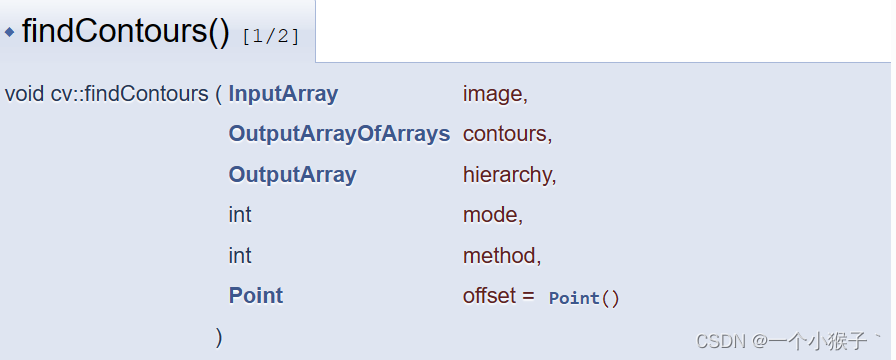
在这里插入图片描述

  • 第一个参数：源图像
  • 第二个参数：探测到的轮廓线。每个轮廓线都被存储为一个点的向量。即用point类型的vector表示。
  • 第三个参数：OutputArray类型的hierarchy，可选的输出向量，包含图像的拓扑信息。其作为轮廓数量的表示，包含了许多元素。每个轮廓contours[i]对应4个hierarchy元素hierarchy[i][0]~hierarchy[i][3]，分别表示后一个轮廓、前一个轮廓、父轮廓、内嵌轮廓的 索引编号。如果没有对应项，对应的hierarchy[i]值设置为负数。
  • 第四个参数：int类型的mode，轮廓检索模式
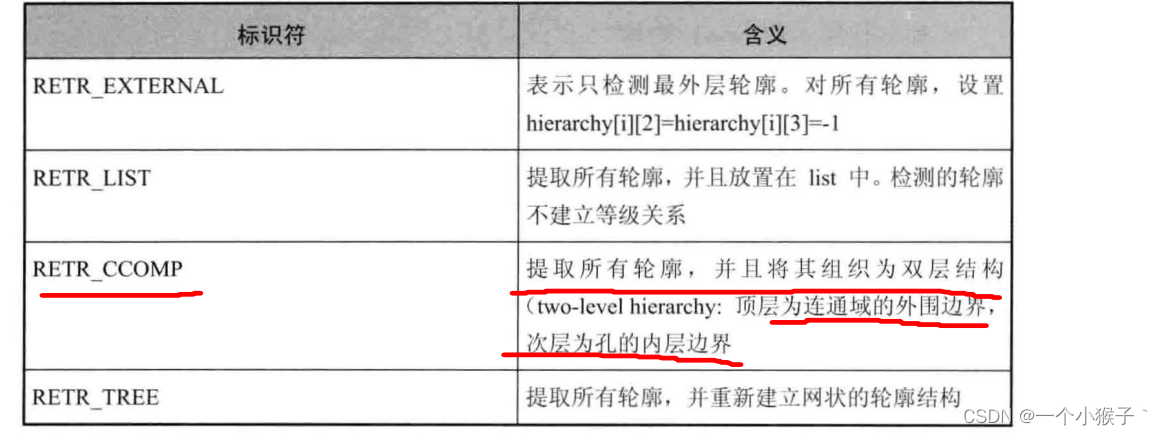
    在这里插入图片描述
  • 第五个参数：int类型的method，为轮廓的近似方法
    在这里插入图片描述
  • 第六个参数：Point类型的offset，每个轮廓的点的可选偏移量，有默认值Point()。对ROI图像中找出的轮廓，并要在整个图像中进行分析时，这个参数便可排上用场。

findContours经常与drawContours配合使用——使用findContours()函数检测到图像轮廓后，便可以用drawContours()函数将检测到的轮廓绘制出来。

1.2 绘制轮廓：drawContours()函数

在这里插入图片描述

  • 第一个参数：目标图像
  • 第二个参数：所有的输入轮廓。每个轮廓存储为一个点向量，即用point类型的vector表示。
  • 第三个参数：int类型的contourIdx，表示要绘制的轮廓的参数。如果它是负数，所有的轮廓都被画出来。
  • 第四个参数：轮廓的颜色
  • 第五个参数：绘制轮廓线的线的厚度。如果它是负数（例如，厚度=FILLED），则绘制轮廓内部。
  • 第六个参数：线条的类型。
  • 第七个参数：关于层次的可选信息。只有在你想只画部分轮廓的时候才需要它（见maxLevel ）。
  • 第八个参数：绘制轮廓的最大水平。如果它是0，只绘制指定的轮廓线。如果它是1，函数会绘制轮廓和所有嵌套的轮廓。如果是2，函数会绘制轮廓、所有嵌套的轮廓、所有嵌套到嵌套的轮廓，以此类推。这个参数只有在有层次的情况下才会被考虑到。
  • 第九个参数：可选的轮廓移动参数。按指定的偏移量=(dx,dy)移动所有绘制的轮廓。

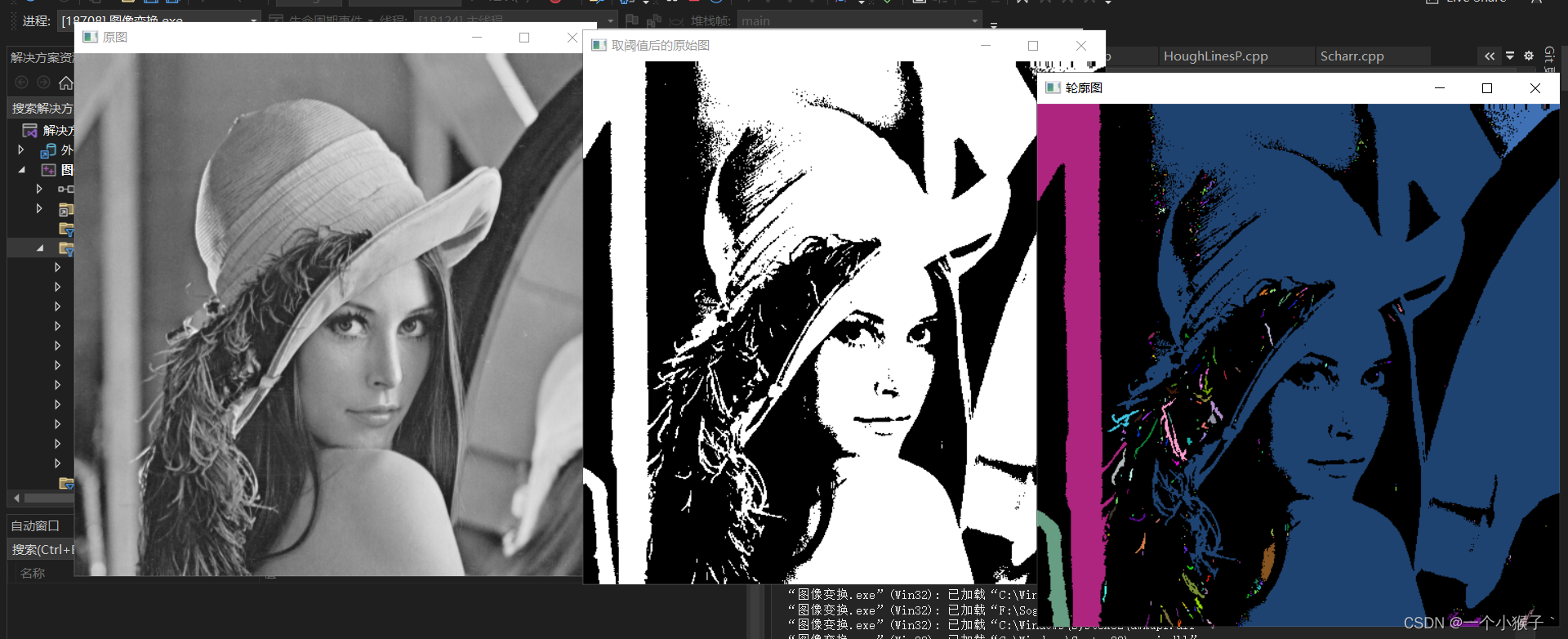
1.3 案例程序：轮廓查找

#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;

int main() {
	
	Mat srcImage = imread("../../image/1.tif",0);
	imshow("原图", srcImage);

	//初始化结果图
	Mat dst = Mat::zeros(srcImage.rows, srcImage.cols, CV_8UC3);

	//srcImage 取大于阈值119的部分
	srcImage = srcImage > 119;
	imshow("取阈值后的原始图", srcImage);

	//定义轮廓和层次结构
	vector<vector<Point>> contours;
	vector<Vec4i> hierarchy;

	//查找轮廓
	findContours(srcImage, contours, hierarchy, RETR_CCOMP, CHAIN_APPROX_SIMPLE);

	//遍历所有顶层的轮廓，以随机颜色绘制出每个连接组件的颜色
	int index = 0;
	for (; index >= 0; index = hierarchy[index][0]) {
		Scalar color(rand() % 255, rand() % 255, rand() % 255);
		drawContours(dst, contours, index, color, FILLED, 8, hierarchy);
	}
	imshow("轮廓图", dst);
	waitKey();

}

在这里插入图片描述

2. 寻找物体的凸包

2.1 凸包

凸包(Convex Hull)是一个计算几何(图形学)中常见的概念。简单来说，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它是能包含点集中所有点的。理解物体形状或轮廓的一种比较有用的方法便是计算一个物体的凸包，然后计算其凸缺陷。很多复杂物体的特性能很好地被这种缺陷表现出来。
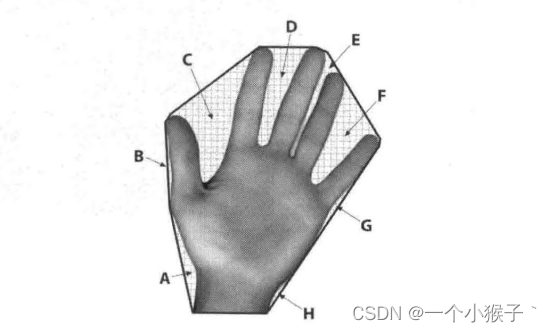
如下图，我们用人手图来说明凸缺陷这一概念。手周围深色的线描画出了凸包，A到H被标出的区域是凸包的各个"缺陷"。正如看到的，这些凸度缺陷提供了手以及手状态的特征表现的方法。
在这里插入图片描述

2.2 寻找凸包：convexHull()函数

在这里插入图片描述

  • 第一个参数：输入二维点集，存储在std::vector或Mat中。
  • 第二个参数：输出参数，函数调用后找到的凸包。
  • 第三个参数：操作方向标识符。当此标识符为真时，输出的凸包为顺时针方向。否则就为逆时针方向。
  • 第四个参数：操作标识符。当标识符为真时，函数返回各凸包的各个点。否则，它返回凸包各点的指数。

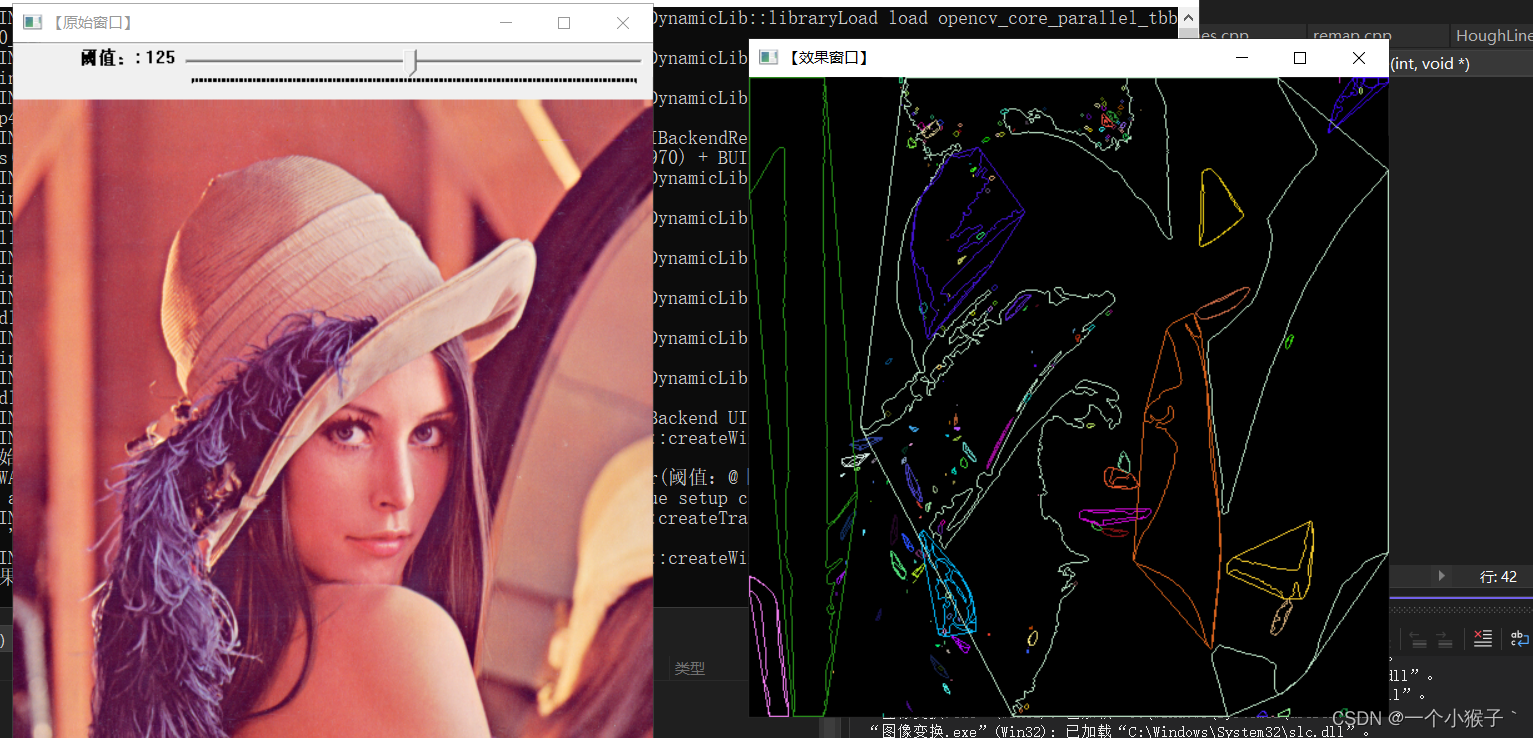
2.3 案例：寻找和绘制物体的凸包

#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;

#define WINDOW_NAME1 "【原始窗口】"
#define WINDOW_NAME2 "【效果窗口】"

//全局变量声明
Mat g_srcImage, g_grayImage;
int g_nThresh = 50;
int g_maxThresh = 255;
RNG g_rng(12345);
Mat srcImage_copy = g_srcImage.clone();
Mat g_thresholdImage_output;
vector<vector<Point>> g_vContours;
vector<Vec4i> g_vHierarchy;

//回调函数thresh_callback()函数
void on_ThreshChange(int, void*) {
	//对图像进行二值化，控制阈值
	threshold(g_grayImage, g_thresholdImage_output, g_nThresh,
		g_maxThresh, THRESH_BINARY);

	//寻找轮廓
	findContours(g_thresholdImage_output, g_vContours, g_vHierarchy, 
		RETR_TREE,CHAIN_APPROX_SIMPLE,Point(0,0));

	//遍历每个轮廓，寻找其凸包
	vector<vector<Point>>  hull(g_vContours.size());
	for (unsigned int i = 0; i < g_vContours.size(); i++) {
		convexHull(Mat(g_vContours[i]), hull[i], false);
	}

	//绘制出轮廓及凸包
	Mat drawing = Mat::zeros(g_thresholdImage_output.size(), CV_8UC3);
	for (unsigned int i = 0; i < g_vContours.size(); i++) {
		Scalar color = Scalar(g_rng.uniform(0, 255), g_rng.uniform(0, 255),
			g_rng.uniform(0, 255));
		drawContours(drawing, g_vContours, i, color, 1, 8, vector<Vec4i>(), 0, Point());
		drawContours(drawing, hull, i, color, 1, 8, vector<Vec4i>(), 0, Point());
	}
	imshow(WINDOW_NAME2, drawing);
}

int main() {
	g_srcImage = imread("../../image/1.tif");
	cvtColor(g_srcImage, g_grayImage, COLOR_BGR2GRAY);
	blur(g_grayImage, g_grayImage, Size(3, 3));
	imshow(WINDOW_NAME1, g_srcImage);

	//创建滚动条
	createTrackbar("阈值：", WINDOW_NAME1, &g_nThresh, g_maxThresh, on_ThreshChange);

	//调用一次进行初始化
	on_ThreshChange(0, 0);
	waitKey(0);
	return 0;
}

在这里插入图片描述

3.使用多边形将轮廓包围

3.1 返回外部矩形边界：boundingRect()函数

此函数计算返回指定点集最外面的矩形边界
Rect boundingRect(InputArray points)

唯一的参数是输入灰度图像或二维点集，存储在std::vector或Mat中。

3.2 寻找最小包围矩形：minAreaRect()函数

此函数用于对给定的2D点集，寻找可旋转的最小面积的包围矩形。
RotatedRect minAreaRect(InputArray points)
唯一的参数是输入灰度图像或二维点集，存储在std::vector或Mat中。

3.3 寻找最小包围圆形：minEnclosingCircle()函数

利用一种迭代算法，对给定的2D点集，去寻找面积最小的可包围它们的圆形。
void minEnclosingCircle(InputArray points,Point2f &center, float& radius)

  • 第一个参数：输入的二维点集
  • 第二个参数：圆的输出中心
  • 第三个参数：圆的输出半径。

3.4 用椭圆拟合二维点集：fitEllipse()函数

RotatedRect fitEllipse (InputArray points)

3.5 逼近多边形曲线：approxPolyDP()函数

void approxPolyDp(InputArray curve, OutputArray approxCurve, double epsilon, bool closed)

  • 第一个参数：输入的二维点集
  • 第二个参数：多边形逼近的结果
  • 第三个参数：逼近的精度
  • 第四个参数：bool类型的closed，如果其为真，则近似的曲线为封闭曲线（第一个顶点和最后一个顶点相连），否则，近似的曲线不封闭。

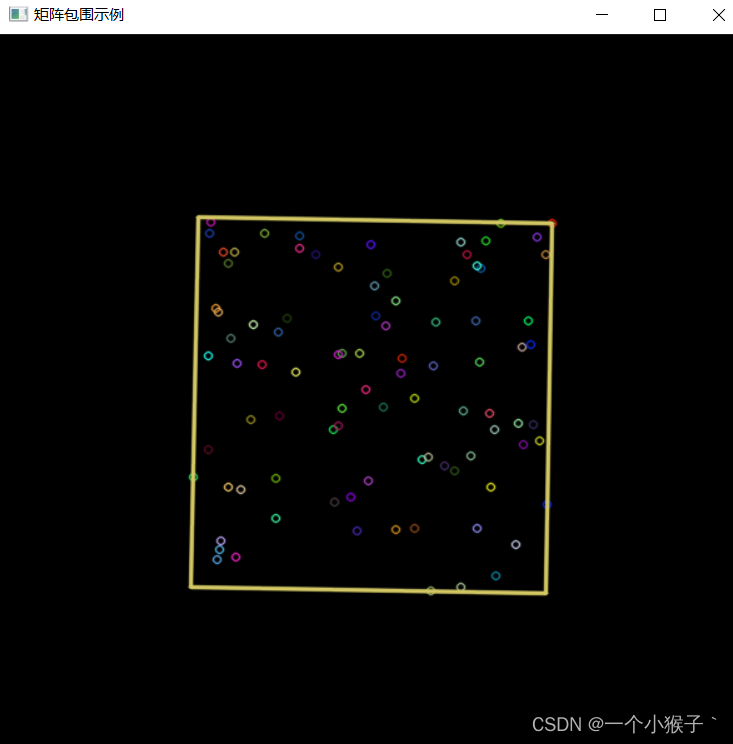
3.6 示例程序：创建包围轮廓的矩形边界

#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;

int main() {
	Mat image(600, 600, CV_8UC3);
	RNG& rng = theRNG();

	//循环，按下ESC，Q，q程序会退出，否则有按键会一直更新
	while (1) {
		int count = rng.uniform(3, 103); //随机生成点的数量
		vector<Point> points; //点值

		for (int i = 0; i < count; i++) {
			Point point;
			point.x = rng.uniform(image.cols / 4, image.cols * 3 / 4);
			point.y = rng.uniform(image.rows / 4, image.rows * 3 / 4);

			points.push_back(point);
		}

		//对给定的2D点集，寻找最小面积的包围矩阵
		RotatedRect box = minAreaRect(Mat(points));
		Point2f vertex[4];
		box.points(vertex);

		//绘制出随机颜色的点
		image = Scalar::all(0);
		for (int i = 0; i < count; i++) {
			circle(image, points[i], 3, Scalar(rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255)),1, LINE_AA);
		}
		
		//绘制出最小面积的包围矩阵
		for (int i = 0; i < 4; i++) {
			line(image, vertex[i], vertex[(i + 1) % 4], Scalar(100, 200, 211), 2, LINE_AA);
		}
		imshow("矩阵包围示例", image);

		//按下ESC或者q、Q程序退出
		char key = (char)waitKey();
		if (key == 27 || key == 'q' || key == 'Q')
			break;
	}
	return 0;
}

在这里插入图片描述

4. 图像的矩

矩函数在图像分析中有着广泛的应用，如模式识别、目标分类、目标识别与方位估计、图像编码与重构等。一个从一幅数字图像中计算出来的矩集，通常描述了该图像形状的全局特征，并提供了大量的关于该图像不同类型的几何特性信息，比如大小、位置、方向及形状等。图像矩的这种特性描述能力被广泛地应用在各种图像处理、计算机视觉和机器人技术领域的目标识别与方位估计中。一阶矩与形状有关，二阶矩显示曲线围绕直线平均值的扩展程度，三阶矩则是关于平均值的对称性的测量。由二阶矩和三阶矩可以导出一组共7个不变矩。而不变矩是图像的统计特性，满足平移、伸缩、旋转均不变的不变性，在图像识别领域得到了广泛的应用。

  • moments计算图像所有的矩（最高到3阶）
  • contourArea计算轮廓面积
  • arcLength来计算轮廓或曲线长度

4.1 矩的计算：moments()函数

moments()函数用于计算多边形和光栅形状的最高达三阶的所有矩。矩用来计算形状的中心、面积、主轴和其他形状特征。
Moments moments(InputArray array, bool binaryImage=false)

  • 第一个参数：输入参数，可以是光栅图像(单通道，8位或浮点的二维数组)或二维数组。
  • 第二个参数：bool类型的binaryImage，有默认值false。若此参数取true，则所有非零像素位为1。此参数仅对于图像使用。

4.2 计算轮廓面积：contourArea()函数

double contourArea(InputArray contour, bool oriented=false)

  • 第一个参数：InputArray类型的contour，输入的向量，二维点(轮廓顶点)，可以为std::vector或Mat类型。
  • 第二个参数：面向区域标识符。若其为true，该函数返回一个带符号的面积值，其正负取决于轮廓的方向。

4.3 计算轮廓长度：arcLength()函数

double arcLength(InputArray curve, bool closed)

  • 第一个参数：InputArray类型的curve，输入的二维点集，可以为std::vector或Mat类型。
  • 第二个参数：bool类型的closed，一个用于指示曲线是否封闭的标识符。

5. 分水岭算法

在这里插入图片描述

5.1 实现分水岭算法：watershed()函数

函数watershed实现的分水岭算法是基于标记的分割算法中的一种。在把图像传给函数之前，我们需要大致勾画标记出图像中的期望进行分割的区域，他们被标记为正指数。所以，每一个区域都会被标记为像素值1、2、3等，表示成为一个或多个连接组件。这些标记的值可以使用findContours()函数和drawContours()函数由二进制掩码检索出来。不难理解，这些标记就是即将绘制出来的分割区域的“种子”，而没有标记清楚的区域，被置为0。在函数输出中，每一个标记中的像素被设置为种子的值，而区域间的值被设置为-1。
在这里插入图片描述

6. 图像修补

6.1 图像修补函数:inpaint()

SSS

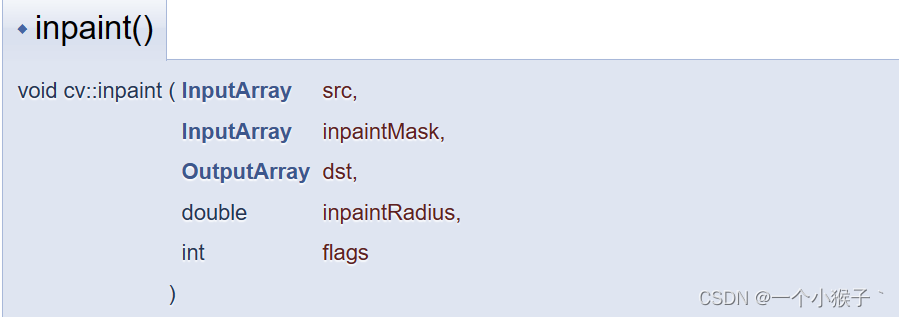
  • 第一个参数：输入图像
  • 第二个参数：修复掩膜,为8位的单通道图像。其中的非零像素表示需要修补的区域。
  • 第三个参数：输出图像
  • 第四个参数：算法所考虑的每个被涂抹的点的圆形邻域的半径。
  • 第五个参数：修补方法的标识

6.2 图像修补案例

#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;

#define WINDOW_NAME1 "原始图"
#define WINDOW_NAME2 "修补后的效果图"

Mat srcImage1, inpaintMask;
Point previousPoint(-1, -1);

//响应鼠标消息的回调函数
static void On_Mouse(int event, int x, int y, int flags, void*) {
	//鼠标左键弹起的消息
	if (event == EVENT_LBUTTONUP || !(flags & EVENT_FLAG_LBUTTON))
		previousPoint = Point(-1, -1);
	//鼠标左键摁下
	else if (event == EVENT_LBUTTONDOWN)
		previousPoint = Point(x, y);

	//鼠标摁下并移动，进行绘制
	else if (event == EVENT_MOUSEMOVE && (flags & EVENT_LBUTTONDOWN)) {
		Point pt(x, y);
		if (previousPoint.x < 0)
			previousPoint = pt;
		//绘制白色线条
		line(inpaintMask, previousPoint, pt, Scalar::all(255), 5, 8, 0);
		line(srcImage1, previousPoint, pt, Scalar::all(255), 5, 8, 0);
		previousPoint = pt;
		imshow(WINDOW_NAME1, srcImage1);
	}
}

int main() {
	Mat srcImage = imread("../../image/1.tif", 1);
	srcImage1 = srcImage.clone();
	inpaintMask = Mat::zeros(srcImage1.size(),CV_8U);
	imshow(WINDOW_NAME1, srcImage1);

	//设置鼠标回调消息
	setMouseCallback(WINDOW_NAME1, On_Mouse, 0);

	while (1) {
		char c = (char)waitKey();
		//Esc:退出		
		if (c == 27)
			break;
		//2:恢复成原始图像
		if (c == '2') {
			inpaintMask = Scalar::all(0);
			srcImage.copyTo(srcImage1);
			imshow(WINDOW_NAME1, srcImage1);
		}

		//1进行修复
		if (c == '1' || c==' ') {
			Mat inpaintedImage;
			inpaint(srcImage1, inpaintMask, inpaintedImage, 3, INPAINT_TELEA);
			imshow(WINDOW_NAME2, inpaintedImage);
		}
	}

	return 0;
}

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/699750.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【前端｜CSS系列第1篇】CSS零基础入门之CSS的基本概念和选择器

【前端｜CSS系列第1篇】CSS零基础入门之CSS的基本概念和选择器

欢迎来到CSS零基础入门系列的第一篇博客&#xff01;在这个系列中&#xff0c;我们将一起学习CSS&#xff08;层叠样式表&#xff09;的基础知识&#xff0c;探索如何为网页添加样式和布局。本篇博客将重点介绍CSS的基本概念和选择器&#xff0c;帮助你理解CSS的核心概念。 1.…
阅读更多...
MAYA活塞（使用骨骼）

MAYA活塞（使用骨骼）

复制骨骼 P父子关系 创建组
阅读更多...
根据数组中对象的某个字段分组最简洁方式

根据数组中对象的某个字段分组最简洁方式

使用map数据结构的&#xff0c;键值唯一性进行操作 //根据年龄分组&#xff0c;获取目标数据格式//[{key:key,data:[{}]}]//{key:[]}const arr [{ name:test1,age:10},{ name:test2,age:20},{ name:test3,age:10},{ name:test4,age:20},{ name:test5,age:10},{ name:test6,age…
阅读更多...
群晖 NAS WebDAV服务手机ES文件浏览器远程访问

群晖 NAS WebDAV服务手机ES文件浏览器远程访问

文章目录 1. 安装启用WebDAV2. 安装cpolar3. 配置公网访问地址4. 公网测试连接5. 固定连接公网地址6. 使用固定地址测试连接 转载自cpolar极点云文章&#xff1a;群晖NAS搭建WebDAV服务手机ES文件浏览器远程访问 有时候我们想通过移动设备访问群晖NAS 中的文件,以满足特殊需求,…
阅读更多...
centos7安装zabbix v4

centos7安装zabbix v4

1.获取rpm包 wget -c https://mirrors.aliyun.com/zabbix/zabbix/4.0/rhel/7/x86_64/zabbix-release-4.0-2.el7.noarch.rpm 2.安装 yum install zabbix-release-4.0-2.el7.noarch.rpm -y 3.关防火墙和selinux 4.下载数据库 yum install mariadb -y 5.启动数据库设置密码 …
阅读更多...
UE4 Cesium离线生成地形

UE4 Cesium离线生成地形

地理空间数据云 首先进这个网址&#xff0c;下载对应的tif以及高程&#xff08;DEM&#xff09; 下载CesiumLab2 在地形切片中点击添加&#xff0c;将黑白图像数据&#xff0c;添加&#xff0c;选择存储类型为散列文件&#xff0c;选择输出路径 再选择影像切片&#xff0c;选择…
阅读更多...
Redis 数据类型 | Navicat 数据编辑器

Redis 数据类型 | Navicat 数据编辑器

Redis 有别于其他键值&#xff08;key-value&#xff09;存储的一个关键特性是它支持多种数据类型&#xff0c;包括字符串&#xff08;string&#xff09;、列表&#xff08;list&#xff09;、集合&#xff08;set&#xff09;、排序集合&#xff08;sorted set&#xff09;和…
阅读更多...
Sparse Fuse Dense: 向高质量的深度补全3D目标检测迈进

Sparse Fuse Dense: 向高质量的深度补全3D目标检测迈进

点云的稀疏性&#xff1a;在远距离和遮挡区域提供的信息较差&#xff0c;导致难以生成精确的3D边界框。 出现了多模态融合。 图像和点云的不同表示方式使得它们难以融合&#xff0c;导致性能不佳。 论文提出了一种新颖的多模态框架SFD&#xff08;Sparse Fuse Dense&#xf…
阅读更多...
Docker学习笔记14

Docker学习笔记14

容器镜像在Docker host的存储位置&#xff1a; 最上面的层&#xff08;layer&#xff09;为读写层&#xff0c;也就是容器。下面的其他的层都是只读层的镜像层。并且除了最下面的一层外&#xff0c;其他的层都有一个指针指向自己下面的一层镜像&#xff08;联合文件系统&#…
阅读更多...
SpringMVC入门篇2 --- 请求与响应

SpringMVC入门篇2 --- 请求与响应

目录 1.请求映射路径 在类上面统一设置RequestMapping注解&#xff0c;统一设置访问路径前缀。 在上文案例的基础上进行修改。 src/main/java/org/example/controller/UserController.java package org.example.controller;import org.springframework.stereotype.Controll…
阅读更多...
寻寻觅觅，彩电厂商能否“智”取未来？

寻寻觅觅，彩电厂商能否“智”取未来？

彩电业&#xff0c;还能不能好&#xff1f; 电视行业的发展&#xff0c;一直伴随着漫长的价格战。从黑白到彩电再到超大屏&#xff0c;从CRT到平板再到液晶&#xff0c;在每一轮技术革新之后&#xff0c;市场总会经历从落到起&#xff0c;从起到落的循环&#xff0c;然后陷入价…
阅读更多...
重磅！2023年影响因子正式发布 , Nature/Science等顶刊普遍下降 (附名单下载)~

重磅！2023年影响因子正式发布 , Nature/Science等顶刊普遍下降 (附名单下载)~

2023年6月28日&#xff0c;科睿唯安&#xff08;Clarivate Analytics&#xff09;发布了最新年度期刊引证报告(JCR), 其中包含我们所关注的最新影响因子(Impact Factor, IF). 科研界对每年影响因子发布可谓是翘首以待&#xff0c;据小编统计发现&#xff0c;今年的影响因子普遍…
阅读更多...
安科瑞故障电弧探测器在建筑电气的设计与应用

安科瑞故障电弧探测器在建筑电气的设计与应用

安科瑞 崔丽洁 【摘要】&#xff1a;电气设备是建筑中不可缺少的一部分&#xff0c;具有较为重要的作用和意义&#xff0c;在应用过程中不仅能够提升建筑本身实用性能&#xff0c;而且可为消费者提供更加优良的生活环境。但设备一旦在运行过程中出现故障&#xff0c;不仅会影响…
阅读更多...
使用python3的sqlalchemy+sqlcipher3对sqlite3数据加密，使用pysqlcipher3编译打建环境，并写项目测试

使用python3的sqlalchemy+sqlcipher3对sqlite3数据加密，使用pysqlcipher3编译打建环境，并写项目测试

一、背景 最近有个想法&#xff0c;想写一个软件&#xff0c;前期本来想用java的springboot加vue来实现&#xff0c;数据库选sqlite来存储&#xff0c;但在用spingboot框架搭好之后&#xff0c;感觉这款软件更适合用python来写&#xff0c;java不适windows桌面系统&#xff0c…
阅读更多...
Spring Boot 中的 Environment

Spring Boot 中的 Environment

Spring Boot 中的 Environment 在 Spring Boot 中&#xff0c;Environment 是一个重要的组件&#xff0c;用于管理应用程序的配置。它是一个接口&#xff0c;提供了访问应用程序配置属性的方法。在本文中&#xff0c;我们将深入探讨 Spring Boot 中的 Environment&#xff0c;…
阅读更多...
Git基本操作总结

Git基本操作总结

0.Git操作关系图 1.初次创建仓库 1)git ini&#xff08;初次提交时使用&#xff0c;项目中会生成.git文件&#xff09; 2)git add . 3)git commit -m “提交代码” 4)git remote add origin “http://xxx.git”&#xff08;关联远程主机&#xff09; / git remote rm origin …
阅读更多...
服务器数据恢复-NetApp FAS存储误删文件夹的数据恢复案例

服务器数据恢复-NetApp FAS存储误删文件夹的数据恢复案例

NetApp存储故障&分析&#xff1a; 某公司一台NetApp存储&#xff0c;工作人员误操作删除一个重要的文件夹。 虽然被删除已经有一段时间了&#xff0c;但是根据NetApp文件系统WAFL的特点&#xff0c;数据被覆盖的可能性不大。 NetApp存储数据恢复过程&#xff1a; 1、由于不…
阅读更多...
自学黑客（网络安全），一般人我劝你还是算了吧（自学网络安全学习路线--第二十章 欺骗攻击及防御技术上）【建议收藏】

自学黑客（网络安全），一般人我劝你还是算了吧（自学网络安全学习路线--第二十章 欺骗攻击及防御技术上）【建议收藏】

文章目录 一、自学网络安全学习的误区和陷阱二、学习网络安全的一些前期准备三、自学网络安全学习路线一、概述二、IP欺骗及防御技术1、基本的IP欺骗2、源路由攻击3、IP欺骗的高级应用——TCP会话劫持4、TCP三步握手连接建立5、TCP会话劫持过程6、IP欺骗攻击的防御7、防范源路由…
阅读更多...
【实用工具】MapStruct—性能无限接近原生手写的对象转换工具

【实用工具】MapStruct—性能无限接近原生手写的对象转换工具

文章目录 优秀借鉴 1、引入2、什么是MapStruct2.1、概述2.2、横向对比2.3、优势 3、快速入门3.1、Maven3.2、POJO3.3、统一映射接口3.4、业务映射接口3.5、测试3.6、输出 4、简单分析5、拓展使用 优秀借鉴 What is a Data Transfer Object (DTO)?Java bean mappings, the easy…
阅读更多...
多元回归预测 | Matlab北方苍鹰算法(NGO)优化极限学习机ELM回归预测，NGO-ELM回归预测，多变量输入模型

多元回归预测 | Matlab北方苍鹰算法(NGO)优化极限学习机ELM回归预测，NGO-ELM回归预测，多变量输入模型

文章目录 效果一览文章概述部分源码参考资料效果一览 文章概述 多元回归预测 | Matlab北方苍鹰算法(NGO)优化极限学习机ELM回归预测，NGO-ELM回归预测，多变量输入模型 评价指标包括:MAE、RMSE和R2等，代码质量极高，方便学习和替换数据。要求2018版本及以上。 部分源码 %% 清…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023