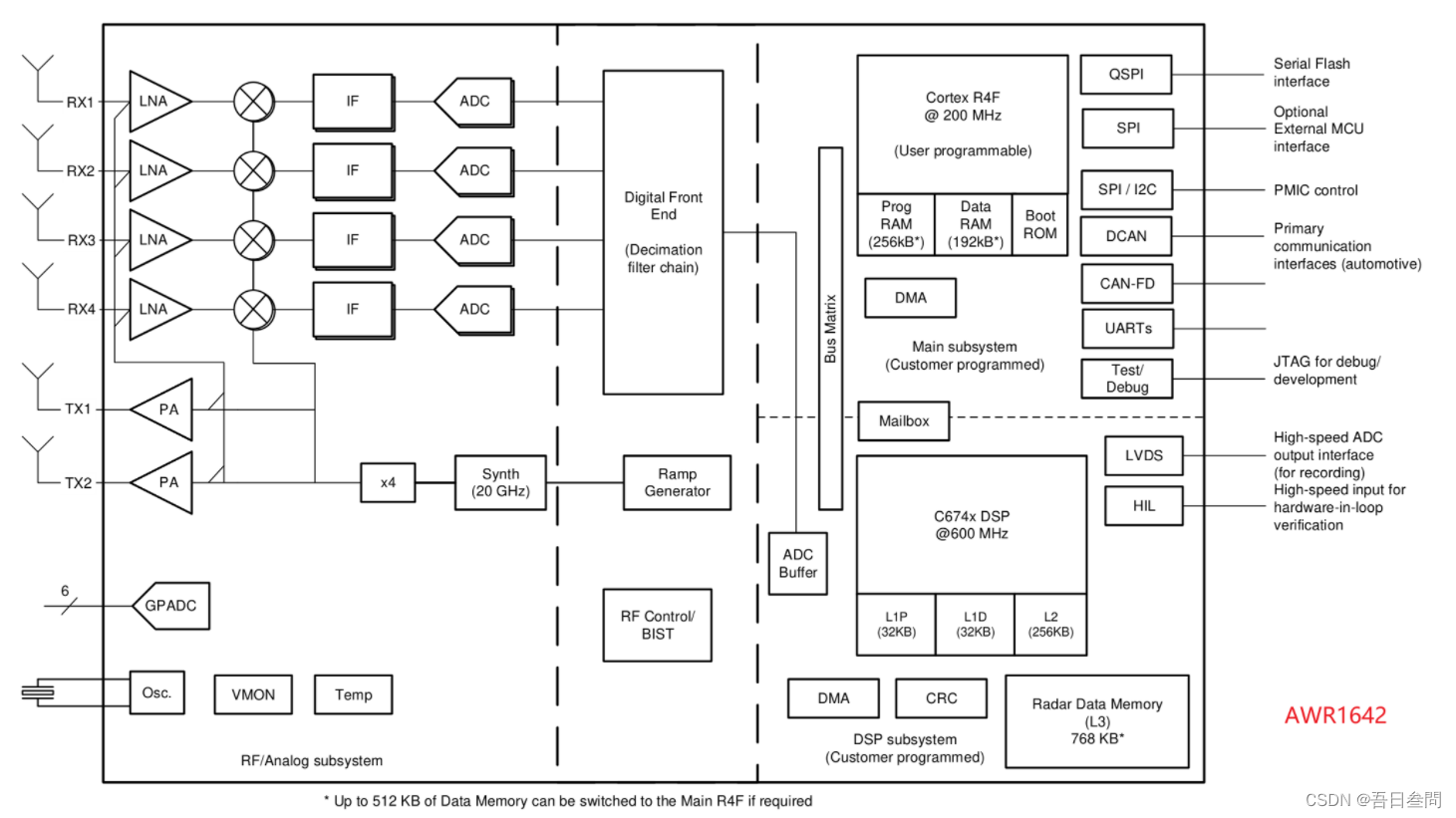
主成分分析(PCA)是一种数据降维技巧,它能将大量相关变量转化为一组很少的不相关变量,这些无关变量称为主成分。最近我们被客户要求撰写关于主成分分析(PCA)的研究报告,包括一些图形和统计输出。例如,使用PCA可将30个相关(很可能冗余)的环境变量转化为5个无关的成分变量,并且尽可能地保留原始数据集的信息。
主成分分析模型,变量(X1到X5)映射为主成分(PC1,PC2)
PCA分析的一般步骤如下:
- 数据预处理。PCA根据变量间的相关性来推导结果。用户可以输入原始数据矩阵或者相关系数矩阵到principal()和fa()函数中进行计算,在计算前请确保数据中没有缺失值。
- 判断要选择的主成分数目(这里不涉及因子分析)。
- 选择主成分(这里不涉及旋转)。
- 解释结果。
- 计算主成分得分。
主成分分析PCA降维方法和R语言分析葡萄酒可视化实例
主成分分析PCA降维方法和R语言分析葡萄酒可视化实例
,时长04:30
PCA的目标是用一组较少的不相关变量代替大量相关变量,同时尽可能保留初始变量的信息,这些推导所得的变量称为主成分,它们是观测变量的线性组合。如第一主成分为:
它是k个观测变量的加权组合,对初始变量集的方差解释性最大。第二主成分也是初始变量的线性组合,对方差的解释性排第二,同时与第一主成分正交(不相关)。后面每一个主成分都最大化它对方差的解释程度,同时与之前所有的主成分都正交.我们都希望能用较少的主成分来解释全部变量。
数据集USJudgeRatings包含了律师对美国高等法院法官的评分。数据框包含43个样本,12个变量:
那么问题来了:是否能够用较少的变量来总结这12个变量评估的信息呢?如果可以,需要多少个?如何对它们进行定义呢?
首先判断主成分的数目,这里使用Cattell碎石检验,表示了特征值与主成数目的关系。一般的原则是:要保留的主成分的个数的特征值要大于1且大于平行分析的特征值。我们直接作图:
评价美国法官评分中要保留的主成分个数。碎石图(直线与x符号)、特征值大于1准则(水平线)和100次模拟的平行分析(虚线)都表明保留一个主成分即可
可以看出只有左上交Component Number为1的特征值是大于1且大于平行分析的特征值的。所以选择一个主成分即可保留数据集的大部分信息。下一步是使用principal()函数挑选出相应的主成分。
可以看出第一主成分(PC1)基本与每个变量都高度相关(除了CONT),也就是说,它是一个可用来进行一般性评价的维度。 h2栏指成分公因子方差——主成分对每个变量的方差解释度。u2栏指成分唯一性——方差无法被主成分解释的比例(1-h2)。 SS loadings行包含了与主成分相关联的特征值,指的是与特定主成分相关联的标准化后的方差值(本例中,第一主成分的值为10)。最后,Proportion Var行表示的是每个主成分对整个数据集的解释程度。此处可以看到,第一主成分解释了12个变量84%的程度。
PC1$scores
主成分得分
由于变量CONT与PC1的相关性太低,即PC1无法代表CONT,所以我们增加一个主成分PC2来代表CONT,结合上期的推送,作图如下:
可以看出,PC1(84.4%)和PC2(9.2%)共可以解释这12个变量的93.6的程度,除了CONT外的其他的11个变量与PC1都有较好的相关性,所以PC1与这11个变量基本斜交,而CONT不能被PC1表示,所以基本与PC1正交垂直,而PC2与CONT基本平行,表示其基本可以表示CONT。