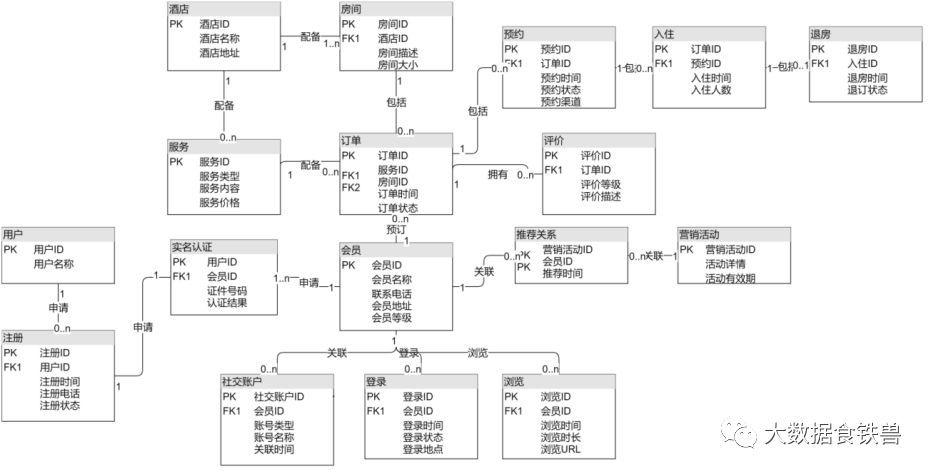
一、回溯算法介绍：一种通过穷举来解决问题的方法，它的核心思想是从一个初始状态出发，暴力搜索所有可能的解决方案，当遇到正确的解则将其记录，直到找到解或者尝试了所有可能的选择都无法找到解为止。

通常采用「深度优先搜索」来遍历解空间（DFS）。在二叉树章节中提到的前序、中序和后序遍历都属于深度优先搜索。

例题一：给定一个二叉树，搜索并记录所有值为 7 的节点，返回节点列表。

 例题二：在二叉树中搜索所有值为 7 的节点，返回根节点到这些节点的路径。

 当走过左下角的节点之后，就会从路径中删掉左下角这个点，并且回到左下角的父节点，进行root.right的遍历，以此类推

复杂的回溯问题还可以加一些约束条件，如例题三：在二叉树中搜索所有值为 7 的节点，返回根节点到这些节点的路径，路径中不能包含值为 3 的节点。

当遇到node.val为3时，提前终止搜索 

回溯算法框架代码：

record_solution是更新res

make_choice是更新state

 用此框架解问题三：

 

二、回溯算法的应用

1.全排列问题：在给定一个集合（如一个数组或字符串）的情况下，找出这个集合中元素的所有可能的排列。

①给定的数组中无重复元素的情况：

从回溯算法代码的角度看，候选集合 choices 是输入数组中的所有元素，状态 state 是直至目前已被选择的元素。注意，每个元素只允许被选择一次，因此在遍历选择时，应当排除已经选择过的元素。

 ②给定的数组中可能包含重复元素，返回所有不重复的排列

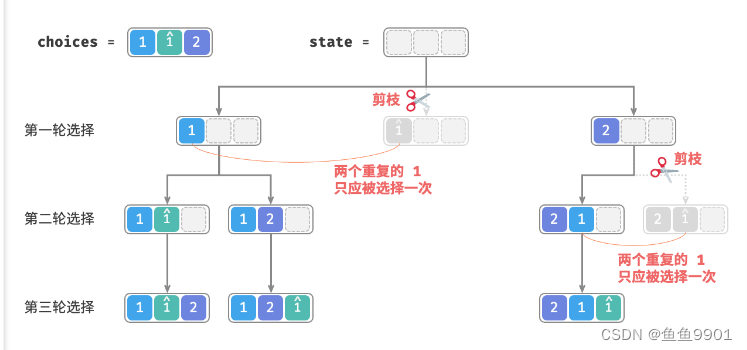
 注意duplicated没有传到backtrack中哦。每轮 backtrack 都包含一个 duplicated 。

 

 假设元素两两之间互不相同，则 n 个元素共有 n! 种排列（阶乘）；在记录结果时，需要复制长度为 n 的列表，使用 O(n) 时间。因此，时间复杂度为 O(n!n) 。

空间复杂度：①是O（n） ②是O（n^2）(因为同一时间可能有n个backtrack中的不同duplicated）

2.子集和问题

①给定一个正整数数组 nums 和一个目标正整数 target ，请找出所有可能的组合，使得组合中的元素和等于 target 。给定数组无重复元素，每个元素可以被选取多次。请以列表形式返回这些组合，列表中不应包含重复组合。

 但这里面可能会有重复的子集，比如{4,5}和{5,4}在这里就被算作了两种子集，所以需要剪枝

 ②给定数组可能包含重复元素，每个元素只可被选择一次。列表中不应包含重复组合和重复元素。

 不允许重复选择元素，所以这里backtrack(state, target - choices[i], choices, i + 1, res)中传回去的不是i而是i+1

 

3.N皇后问题:根据国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。给定 n 个皇后和一个 N×N 大小的棋盘，寻找使得所有皇后之间无法相互攻击的摆放方案。比如：

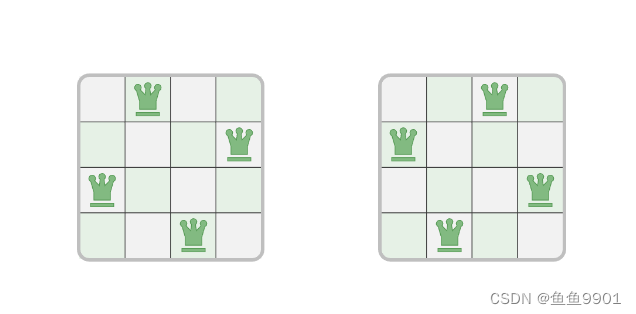
 本题共有三个约束条件：多个皇后不能在同一行、同一列和同一对角线（对角线有两条哦）。

1.逐行放置（剪枝1）

2. 用一个长度为 n的布尔型数组 cols 记录每一列是否有皇后。在每次决定放置前，我们通过 cols 将已有皇后的列剪枝，并在回溯中动态更新 cols 的状态。（剪枝2）

3.若两个格子满足 row1 - col1 == row2 - col2 ，则这两个格子一定处在一条主对角线上。 若row1 + col1 == row2 + col2，则这两个格子一定处在一条次对角线上。（剪枝3）

 

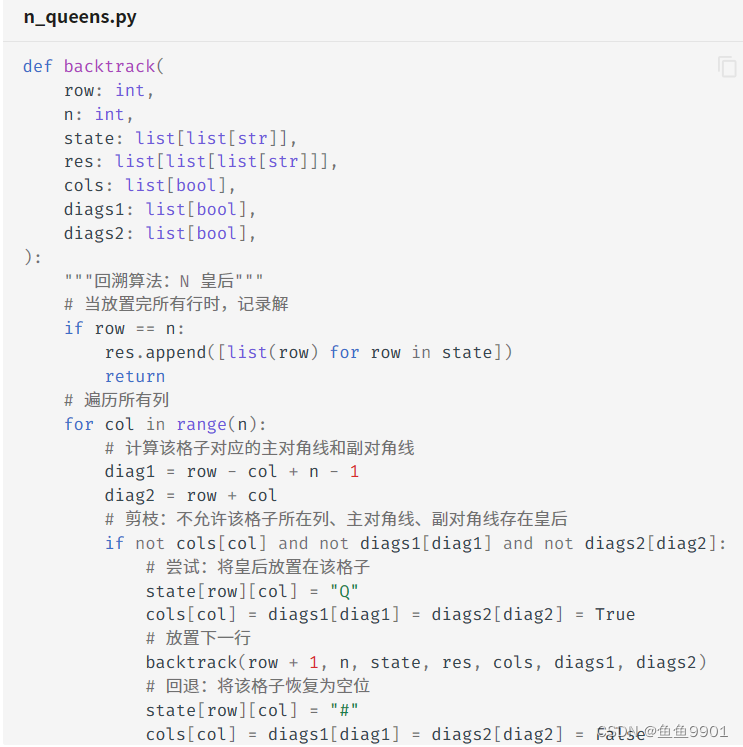
diag1 = row - col + n -1 是因为row - col 最小等于1-n 

时间复杂度O（n!）空间复杂度O（n^2)（state使用O（n^2)的空间）