2015 级考研管理类联考数学真题
一、问题求解(本大题共 15 小题,每小题 3 分,共 45 分)下列每题给出 5 个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。
1.若实数a,b, c 满足
a
:
b
:
c
=
1
:
2
:
5
a:b:c=1:2:5
a:b:c=1:2:5,且a + b + c = 24 ,则
a
2
+
b
2
+
c
2
a^2+b^2+c^2
a2+b2+c2 =( )
A.30
B.90
C.120
D.240
E.270
2.某公司共有甲、乙两个部门.如果从甲部门调10 人到乙部门,那么乙部门人数是甲部门的2 倍;如果把乙部门员工的
1
5
\frac{1}{5}
51调到甲部门,那么两个部门的人数相等.该公司的总人数为( )
A.150
B.180
C.200
D.240
E.250
3.设m, n 是小于20 的质数,满足条件
∣
m
−
n
∣
=
2
|m-n|=2
∣m−n∣=2的{
m
,
n
m,n
m,n}共有( )
A.2 组
B.3 组
C.4 组
D.5 组
E.6 组
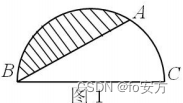
4.如图1, BC 是半圆的直径,且 BC = 4,∠ABC =
3
0
0
30^0
300 ,则图中阴影部分的面积为( )
A.
4
3
π
−
3
\frac{4}{3}π-\sqrt{3}
34π−3
B.
4
3
π
−
2
3
\frac{4}{3}π-2\sqrt{3}
34π−23
C.
2
3
π
+
3
\frac{2}{3}π+\sqrt{3}
32π+3
D.
2
3
π
+
2
3
\frac{2}{3}π+2\sqrt{3}
32π+23
E.
2
π
−
2
3
{2}π-2\sqrt{3}
2π−23
5.在某次考试中,甲、乙、丙三个班的平均成绩分别为80,81和81.5 ,三个班的学生得分之和为6952 ,三个班共有学生( )
A.85 名
B.86 名
C.87 名
D.88 名
E.90 名
6.有一根圆柱形铁管,管壁厚度为0.1 米,内径为1.8 米,长度为2 米,若将该铁管熔化后浇铸成长方体,则该长方体的体积为(单位:
m
3
m^3
m3;π≈3.14 )( )
A.0.38
B.0.59
C.1.19
D.5.09
E.6.28
7.某人驾车从 A 地赶往 B 地,前一半路程比计划多用时45 分钟,平均速度只有计划的80% 。若后一半路程的平均速度为120 千米/小时,此人还能按原定时间到达 B 地. A, B 两地的距离为( )
A.450 千米
B.480 千米
C.520 千米
D.540 千米
E.600 千米
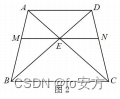
8.如图 2,梯形 ABCD 的上底与下底分别为5, 7 ,E 为 AC 与 BD 的交点,MN 过点 E 且平行于 AD . 则MN ( )
A.
26
5
\frac{26}{5}
526
B.
11
2
\frac{11}{2}
211
C.
35
6
\frac{35}{6}
635
D.
36
7
\frac{36}{7}
736
E.
40
7
\frac{40}{7}
740
9.已知
x
1
,
x
2
x_1,x_2
x1,x2是
x
2
+
a
x
−
1
=
0
x^2+ax-1=0
x2+ax−1=0的两个实根,则
x
1
2
+
x
2
2
x_1^2+x_2^2
x12+x22=( )
A.
a
2
+
2
a^2+2
a2+2
B.
a
2
+
1
a^2+1
a2+1
C.
a
2
−
1
a^2-1
a2−1
D.
a
2
−
2
a^2-2
a2−2
E.
a
+
2
a+2
a+2
10.一件工作,甲、乙合作要2 天,人工费2900 元;乙、丙两人合作需要4 天,人工费2600元;甲、丙两人合作2 天完成了全部工作量的
56,人工费2400 元.甲单独做该工作需要的时间与人工费分别为( )
A.3 天,3000 元
B.3 天,2850 元
C.3 天,2700 元
D.4 天,3000 元
E.4 天,2900 元
11.若直线 y = ax 与圆
(
x
−
a
)
2
+
y
2
=
1
(x-a)^2+y^2=1
(x−a)2+y2=1相切,则
a
2
a^2
a2 = ( )
A.
1
+
3
2
\frac{1+\sqrt{3}}{2}
21+3
B.
1
+
3
2
1+\frac{\sqrt{3}}{2}
1+23
C.
5
2
\frac{\sqrt{5}}{2}
25
D.
1
+
5
2
1+\frac{\sqrt{5}}{2}
1+25
E.
1
+
5
2
\frac{1+\sqrt{5}}{2}
21+5
12.设点 A(0,2)和 B(1,0)在线段 AB 上取一点M(x,y)(0<x<1),则以 x,y 为两边长的矩形面积的最大值为( )
A.
5
8
\frac{5}{8}
85
B.
1
2
\frac{1}{2}
21
C.
3
8
\frac{3}{8}
83
D.
1
4
\frac{1}{4}
41
E.
1
8
\frac{1}{8}
81
13.某新兴产业在 2005 年末至 2009 年末产值的年平均增长率为q ,在 2009 年末至 2013 年末的年平均增长率比前四年下降了40% ,2013 年的产值约为 2005 年产值的
14.46
(
≈
1.9
5
4
)
14.46(≈1.95^4)
14.46(≈1.954)倍,q 约为( )
A.30%
B.35%
C.42%
D.45%
E.50%
- 某次网球比赛的四强对阵为甲对乙、丙对丁,两场比赛的获胜者将争夺冠军. 选手之间相互获胜的概率如下:
| 结果 | 甲 | 乙 | 丙 | 丁 |
|---|---|---|---|---|
| 甲获胜概率 | 0.3 | 0.3 | 0.8 | |
| 乙获胜概率 | 0.7 | 0.6 | 0.3 | |
| 丙获胜概率 | 0.7 | 0.4 | 0.5 | |
| 丁获取概率 | 0.2 | 0.7 | 0.5 |
甲获得冠军的概率为( )
A.0.165
B.0.245
C.0.275
D.0.315
E.0.330
15.平面上有5 条平行直线与另一组n 条平行直线垂直,若两组平行直线共构成280 个矩形,则n =( )
A.5
B.6
C.7
D.8
E.9
二.条件充分性判断:(第 16-25 小题,每小题 3 分,共 30 分)
要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论,A、B、C、D、E 五个选项为判断结果,请选择一项符合试题要求的判断,请在答题卡上将所选的字母涂黑。
(A) 条件(1)充分,但条件(2)不充分
(B) 条件(2)充分,但条件(1)不充分
(C) 条件(1)和(2)都不充分,但联合起来充分
(D) 条件(1)充分,条件(2)也充分
(E) 条件(1)不充分,条件(2)也不充分,联合起来仍不充分
-
圆盘 x 2 + y 2 ≤ 2 ( x + y ) x^2+y^2≤2(x+y) x2+y2≤2(x+y)被直线 L 分成面积相等的两部分.
(1) L:x + y = 2
(2) L:2x - y = 1 -
已知a, b 为实数.则a ≥ 2 或b ≥ 2 .
(1)a + b ≥ 4
(2)ab ≥ 4 -
已知 p, q 为非零实数. 则能确定 p q ( p − 1 ) \frac{p}{q(p-1)} q(p−1)p的值.
(1)p+q=1
(2) 1 p + 1 q = 1 \frac{1}{p}+\frac{1}{q}=1 p1+q1=1 -
信封中装有10 张奖券,只有1张有奖. 从信封中同时抽取2 张奖券,中奖的概率为 P ;从信封中每次抽取1张奖券后放回,如此重复抽取n 次,中奖的概率为Q ,则 P < Q .
(1)n = 2
(2)n = 3 -
设{ a n a_n an}是等差数列,则能确定数列{ a n a_n an}
(1) a 1 + a 6 = 0 a_1+a_6=0 a1+a6=0
(2) a 1 a 6 = − 1 a_1a_6=-1 a1a6=−1 -
已知 M = ( a 1 + a 2 + . . . + a n − 1 ) ( a 2 + a 3 + . . . + a n ) M=(a_1+a_2+...+a{n-1})(a_2+a_3+...+a_n) M=(a1+a2+...+an−1)(a2+a3+...+an), N = ( a 1 + a 2 + . . . + a n ) ( a 2 + a 3 + . . . + a n − 1 ) N=(a_1+a_2+...+a_n)(a_2+a_3+...+a_{n-1}) N=(a1+a2+...+an)(a2+a3+...+an−1),则M>N。
(1) a 1 > 0 a_1>0 a1>0
(2) a 1 a n a_1a_n a1an>0 -
几个朋友外出游玩,购买了一些瓶装水,则能确定购买的瓶装水数量
(1)若每人分3 瓶,则剩余30 瓶
(2)若每人分10 瓶,则只有一人不够 -
已知数列{ a n a_n an}是公差大于零的等差数列,{ S n S_n Sn}是{ a n a_n an}的前n 项和.则 S n ≥ S 10 , n = 1 , 2 , . . . S_n≥S_{10},n=1,2,... Sn≥S10,n=1,2,...
(1) a 10 = 0 a_{10}=0 a10=0
(2) a 11 a 10 < 0 a_{11}a_{10}<0 a11a10<0 -
底面半径为r ,高为h 的圆柱体表面积记为 S 1 S_1 S1,半径为 R 球体表面积记为 S 2 S_2 S2,则 S 1 ≤ S 2 S_1≤S_2 S1≤S2
(1)R≥ r + h 2 {r+h}\over2 2r+h
(2)R≤ r + 2 h 3 {r+2h}\over3 3r+2h -
已知 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3为实数, x x x 为 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3的平均值,则 ∣ x k − x ∣ ≤ 1 , k = 1 , 2 , 3 |x_k-x|≤1,k=1,2,3 ∣xk−x∣≤1,k=1,2,3
(1) ∣ x k ∣ ≤ 1 , k = 1 , 2 , 3 |x_k|≤1,k=1,2,3 ∣xk∣≤1,k=1,2,3
(2) x 1 = 0 x_1=0 x1=0