目录

0.前言

1.什么是OJ

1.1 OJ简述

1.2 OJ的分类（尤其接口型OJ，带你剖析得明明白白）

1.3 接口型OJ的输入型参数

2. 剑指 Offer 56 - I. 数组中数字出现的次数

3. 88. 合并两个有序数组

4. 27.移除元素

5. 26. 删除有序数组中的重复项.

---

0.前言

本文所有代码都已上传至Gitee

1顺序表OJ题 · onlookerzy123456qwq/data_structure_practice_primer - 码云 - 开源中国 (gitee.com)https://gitee.com/onlookerzy123456qwq/data_structure_practice_primer/tree/master/1%E9%A1%BA%E5%BA%8F%E8%A1%A8OJ%E9%A2%98

1.什么是OJ

1.1 OJ简述

OJ主要其实就是我们在刷题网站上，例如leetcode，牛客网，洛谷等所刷的题。

OJ题，也是我们之后校招社招进行笔试的主要形式。

OJ题的判定方式，就是拿你实现的程序，在经过多个测试用例的测试之后，看你程序的运行结果是否全部符合预期。

1.2 OJ的分类（尤其接口型OJ，带你剖析得明明白白）

OJ题主要分为IO型和接口行两类。

IO型最好理解，就是从#include包含头文件，到main函数的实现，到scanf/cin输入数据，以及printf/cout打印结果，都由你自己完成，测试的方式是检测你最终打印出的结果是否符合预期。这个是我们大多数人一开始刷题所最初接触到的一类OJ题。

OJ题还有一种接口型的。接口型OJ说白了就是实现出一个函数，比如我们给了一个int Add(int x,int y)函数让你实现，这就是接口型的OJ。

在接口型的OJ题中，不需要我们#include头文件以及主函数main的实现，这些都不用写，你只需要把这个函数接口实现出来就可以了。那具体是什么技术做到了这一点呢？一个程序肯定必须有main函数进入执行呀，怎么会不需要实现呢？事实上，main函数在服务器当中。

我们是在浏览器上写好了这个函数，然后通过浏览器，通过网络传输到比如Leetcode官网率的服务器当中。而Leetcode的服务器会专门针对这个题，有专门配套的文件。首先你传来的是一个这个函数实现的.c文件，比如ojfunc.c，然后在服务器这里，有一个main.c以及ojfunc.h这两个文件，然后在ojfunc.h中已经声明了这个接口函数，并且已经包好了各种通用的头文件，比如<stdio.h>,<string.h>,<stdlib.h>等，然后main.c中包含了ojfunc.c这个头文件，在main.c中有main函数，main调用这个实现的接口函数，传入测试数据进行测试。

1.3 接口型OJ的输入型参数

 

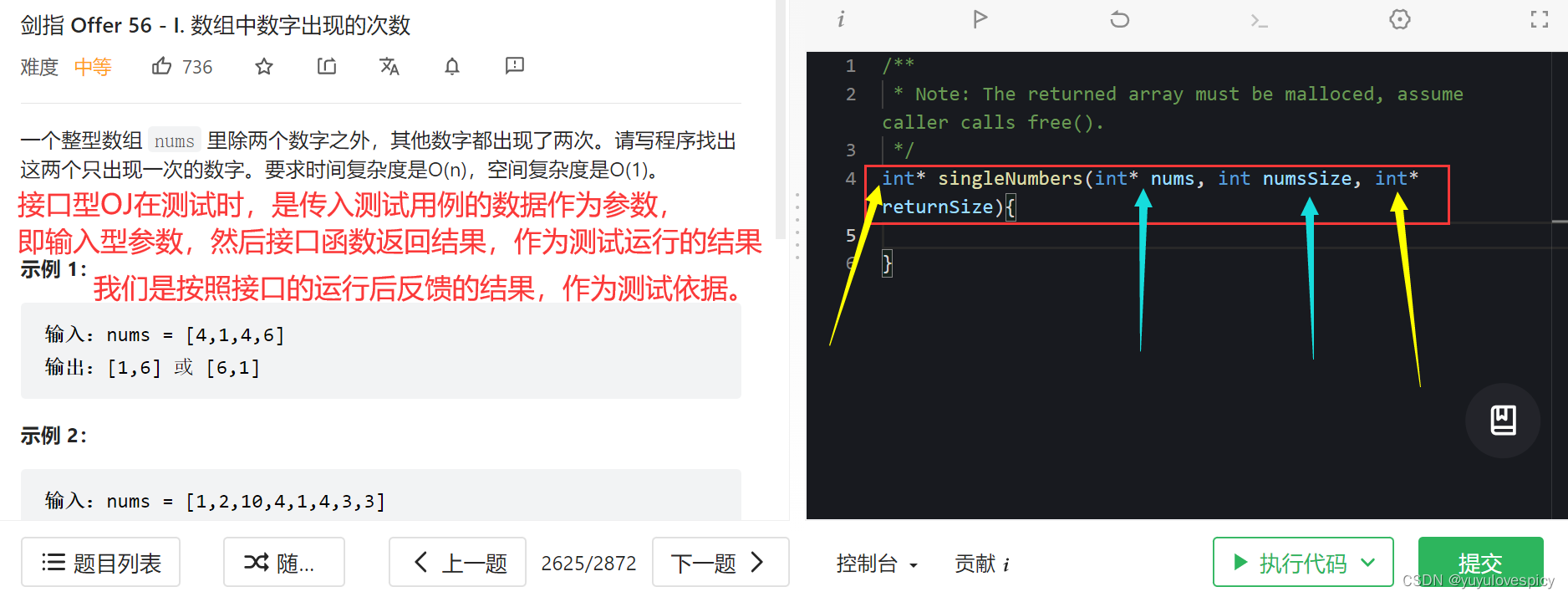
我们实现的一个函数接口，对之传入测试的源数据，然后接口根据传入的数据返回运行的结果，然后就可以根据运行结果与正确的结果进行对照，判断自己实现的接口是否能通过一个个的测试用例。 

接口函数的运行结果，我们是通过这个函数的返回值来获取。可是接口函数的运行结果一定只有一个吗？当然不一定，有时候一个函数接口需要返回多个运行结果，可是函数的返回值只有一个，所以此时我们就需要借助输出型参数。

输出型参数就是，在接口函数的外部定义一个变量，然后在接口函数中传入这个变量的地址，然后解引用这个地址，可以我们在接口函数内部对这个外部的变量进行赋值。所以输出型参数也是一种反馈运行结果的方式。

比如在这个例子当中，返回值int*，就是返回的一个数组指针，int* returnSize，就是输出型参数，代表你返回数组的大小，这两个都是反馈给上层的运行结果。而int* nums,int numsSize就是输入型参数，是上层传给这个接口的数据源，就是一个numsSize大小的nums数组。

2. 剑指 Offer 56 - I. 数组中数字出现的次数

剑指 Offer 56 - I. 数组中数字出现的次数 - 力扣（LeetCode）https://leetcode.cn/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-lcof/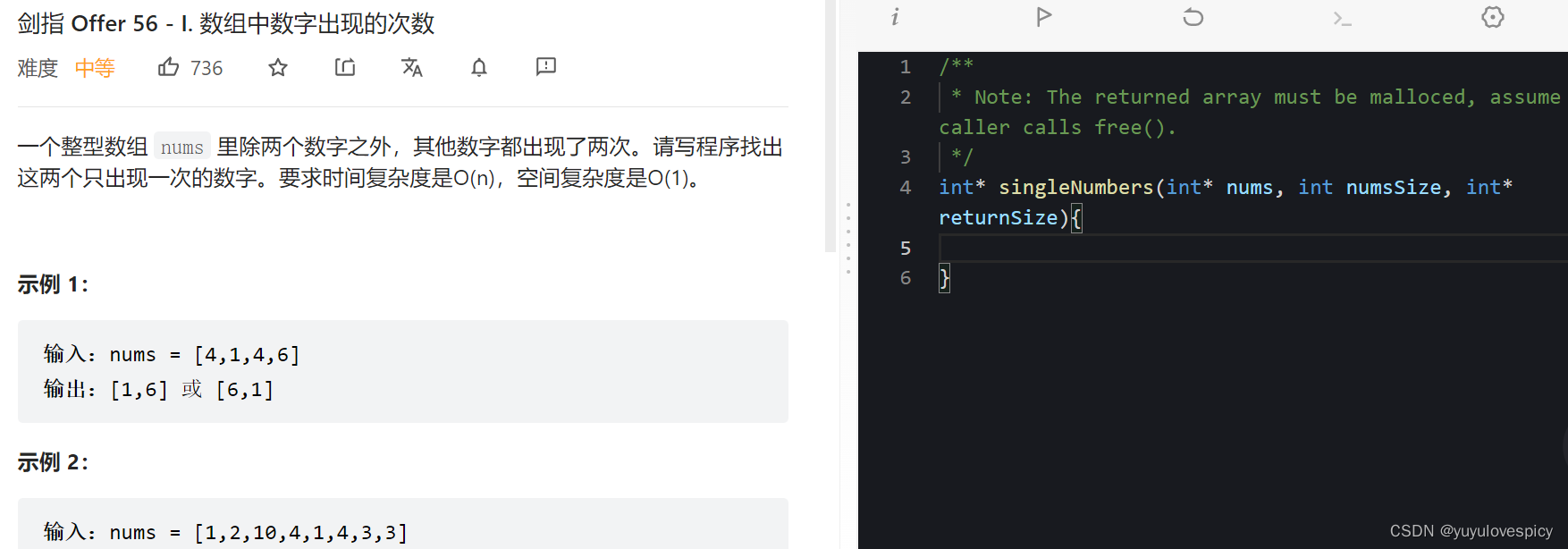

我们首先分析接口的实现，传入的是大小为numsSize的数组nums，然后需要我们返回一个大小为*returnSize的数组指针int*。分析这是找到数组nums当中的两个只出现一次的数，所以我们返回的数组是存储这两个数字的数组，这个数组我们在堆区开辟，最后返回这个数组指针。我们知道这个返回的数组的大小一定是2，所以我们给传入的输出型参数*returnSize的赋值一定是2。

如何找到这个两个只出现一次的数呢？

我们依靠的是异或的特性：

1.两个相同的数异或的值都是0，a^a = 0，b^b = 0，c^c^d^d = 0。

2.任何数异或0，都是这个数，a^0 = a，c^d^d = c^0 = c。

针对要寻找的只出现一次的两个数字，这是两个不同的整形数字，他们32个bit位必定有至少一位是不相同的（因为他们不是同一个数值），所以我们需要找到这是32个bit位的第几个比特位：让nums数组中的所有数异或，最后得到的结果一定是两个只出现一次的数的异或的结果，然后我们根据这个结果的32bit位，找出第一个是1的bit位，这一位就是这两个只出现一次的数，不同的bit位位置。

我们在根据这个bit位的数值，对nums中所有的数进行分类，最后一定是这个bit位是0的数都被分在了一起，bit为都是1的数据都被分在了一组。这两个只出现一次的数必然被分在了两个不同的组中，所有每一个出现两次的同值的数，也必然是分在了同一组。

然后我们对两个组中的所有数进行异或，最后两个组分别异或出的数，就是所求的两个只出现一次的数。

例如 nums[1,2,10,4,1,4,3,3]，2和10的第4个bit位不一样，2的第四个比特位是0，10的第四个比特位是1。所以天然就可以分组为 [1,2,4,1,4,3,3] VS [10]两个组，然后1^2^4^1^4^3^3 = 2，10 = 10。从而得到了这两个只出现一次的数。

int* singleNumbers(int* nums, int numsSize, int* returnSize){
    //找出这两个数字,利用异或的特性，找到a^b的Val
    int ret = 0;
    for(int i=0;i<numsSize;++i)
    {
        ret ^= nums[i];
    }
    //pos标识32bit位中a不同于b的那一位
    int pos = 0;
    for(int i=0;i<32;++i)
    {
        if((ret>>i)&0x1 == 1)
        {
            pos = i;
            break;
        }
    }
    //按照第pos个bit位，分为两位
    int ret1 = 0,ret2=0;
    for(int i=0;i<numsSize;++i)
    {
        if(((nums[i]>>pos)&0x1)==0)
        {
            ret1^=nums[i];
        }
        else //if((nums[i]>>pos)==1)
        {
            ret2^=nums[i];
        }
    }
    //ret1,ret2分别就是两个一次的数
    int *ptmp = (int*)malloc(2*sizeof(int));
    ptmp[0]=ret1;
    ptmp[1]=ret2;
    *returnSize=2;
    return ptmp;
}

3. 88. 合并两个有序数组

88. 合并两个有序数组https://leetcode.cn/problems/merge-sorted-array/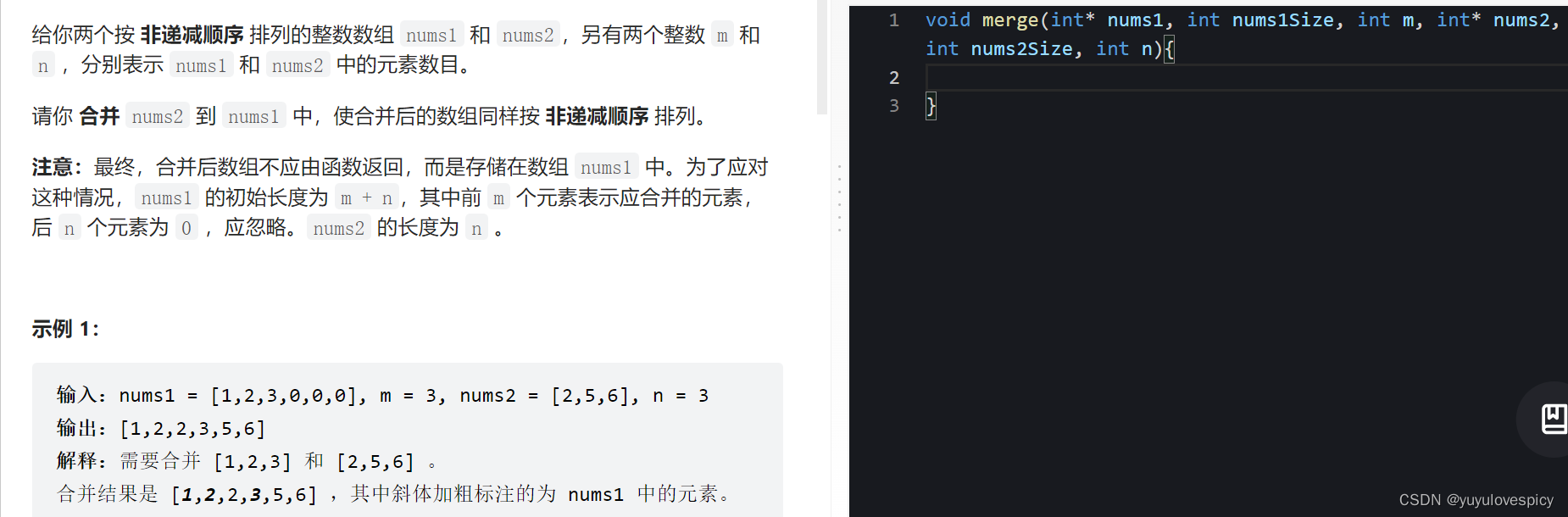

 分析题目的OJ，我们看到题目给了我们一个有有效元素m个的数组nums1，有有效元素n个的数组nums2，nums1，nums2的元素都是升序的，然后我们让两个数组的元素合并到nums1当中（nums1数组有效元素本来有m个，但是可以存nums1Size个元素，即m+n个元素），且按照升序排列。

最简单粗暴的两种方法，第一种是直接把nums2的所有元素，紧接着nums1数组所有元素的后面拷贝过去，然后对nums2进行排序即可，但是这样的时间复杂度就一定会达到O（N*log2N）,这样时间复杂度就太高了。

第二种是把新开辟一块nums1Size，即m+n大小的空间，然后定义两个指针，分别指向nums1和nums2的首，把nums1和nums2的数据比对大小，谁小就填入这个新空间当中，一次比对，直到两个数组都是空，全部填入新空间当中，这时新空间的元素就是对m+n个数据有序排序，最后再把新空间的数据拷贝到nums1中即可，可是这样空间复杂度就达到了O(N)，效果也并不是很好。

我们要在空间复杂度是O(1)，时间复杂度是O(N)的算法下完成这个接口的实现，就需要使用下面这第三种方法。我们设计src1，src2分别指向nums1，和nums2，的最后一个有效数据，作为数据源，然后设计dest指向nums1的末尾，作为填入数据的地方，我们在nums1和nums2这两个数据源中，挑选大的数据选入到dest指向的位置上。哪个作为了一次数据源填入到了dest当中，则哪个src--，同时dest也--，最后到nums2即src2到0最后被赋值完毕之后，最后nums1就是有序的所有m+n个数据的数组。

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
    //m是nums1有效数据个数，n是nums2有效数据个数。
    //从nums1的最后面开始赋值
    int dest = m+n-1;
    int src1 = m-1;
    int src2 = n-1;
    while(src1>=0&&src2>=0)
    {
        if(nums1[src1]<=nums2[src2])
        {
            nums1[dest--] = nums2[src2];
            --src2;
        }
        else{
            nums1[dest--] = nums1[src1];
            --src1;
        }
    }
    //拷贝nums的数据到nums1中一遍[nums1提前被赋值完毕的情况]
    while(src2>=0)
    {
        nums1[dest--]=nums2[src2--];
    }
}

4. 27.移除元素

27. 移除元素https://leetcode.cn/problems/remove-element/

 分析题目：这道OJ题给了我们一个有numsSize有效元素大小的数组nums，然后让我们删除这个数组当中值为int val的值。

首先我们给出暴力的方法，就是直接开辟出来一个数组，然后遍历这个数组，让数组当中的不是val的数据填入到这个新开辟的数组当中，最后这个数组就是去除val的数组。可是这样需要付出O(N)的空间复杂度，这对我们是十分不利的，有没有一种方法可以让我们不开辟新的空间，直接在原数组nums中进行操作呢？

 

我们可以直接把原来的nums当做新开辟的数组空间看！何出此言：我们定义两个指针，一个src，一个dest，src作为数据源，dest作为对nums赋值的指针。src往前寻找非val的值，每次src++往前寻找，如果遇到的是要删除的val数据，就直接++跳过去，如果是非val的有效数据，则会给src位置的数据赋值给dest指向的位置，然后src数据源和dest赋值处同时++往前跳。这样我们就同时把nums作为了数据源，也把nums作为了新开辟的空间，即直接往nums中进行值填充。

int removeElement(int* nums, int numsSize, int val){
    int src = 0;
    int dest = 0;
    while(src<numsSize)
    {
        if(nums[src]!=val)
        {
            nums[dest++]=nums[src++];
        }
        else{
            src++;
        }
    }
    return dest;
}

5. 26. 删除有序数组中的重复项.

26. 删除有序数组中的重复项https://leetcode.cn/problems/remove-duplicates-from-sorted-array/

这个题目中给了有numsSize个数据的nums数组，然后这个数组是升序排序的。要求我们对这个数组进行去重，最后保证这个数组仍然是升序的。而且要求我们 原地修改数组，不开辟额外的空间，即在O(1)的空间复杂度下完成。 

所以我们必须同时把这个数组nums，作为数据源以及作为填充赋值的区域。所以我们仍然需要一个src指针作为数据源，dest指针作为填充值的单元引导。然后我们知道这个nums数组当中，会有连续的重复同等大小的元素，我们不能重复的填入这几个值，这就需要我们再定义一个变量记录这个我们最近一次填入过dest的值，防止重复填入。

src往前探索作为数据源，如果此时和我们记录的最近一次填入过dest的值相同，那就不会填入，如果不同那就是找到了新的数据源，此时就会给dest处赋值，然后dest++，进入下一个赋值处。然后src继续++往前寻找新的数据源，而我们也要更新最近一次填入到dest的值。

int removeDuplicates(int* nums, int numsSize){
    if(numsSize==0||numsSize==1)
    return numsSize;
    int remember_flag = nums[0];
    int dest = 0;
    int src = 0;
    while(src<numsSize)
    {
        if(nums[src]==remember_flag)
        {
            ++src;
        }
        else
        {
            ++dest;
            nums[dest]=nums[src];
            remember_flag = nums[src];
            ++src;
        } 
    }
    return dest+1;
}