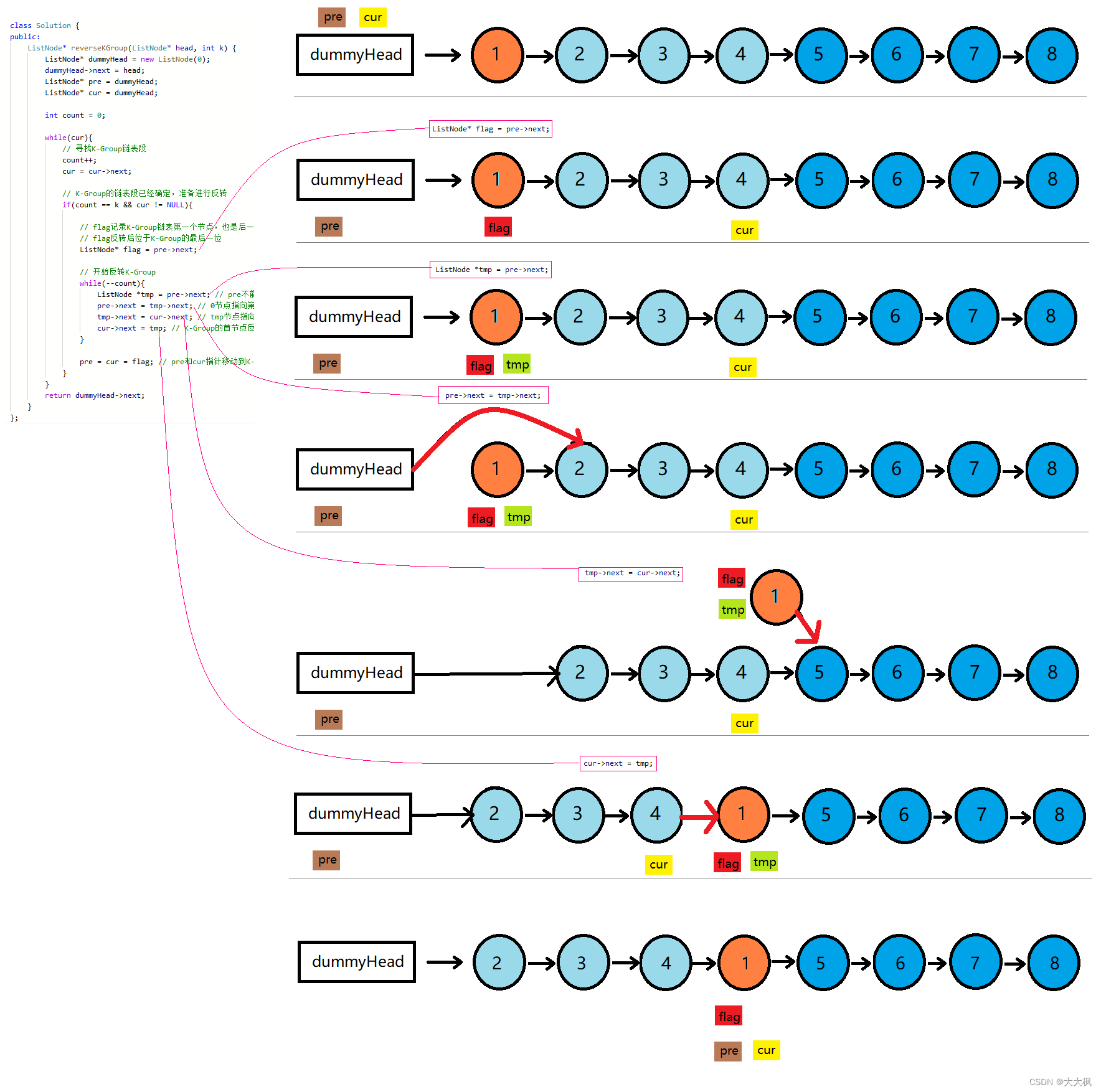
37.解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字 1-9 在每一行只能出现一次。
- 数字 1-9 在每一列只能出现一次。
- 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
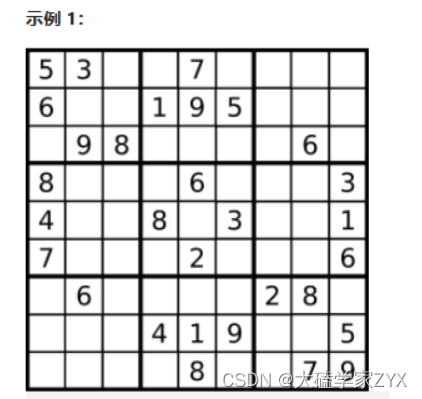
输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:

提示:
board.length== 9board[i].length== 9board[i][j]是一位数字或者'.'- 题目数据 保证 输入数独仅有一个解
思路
本题与之前做过的回溯题目都不同。棋盘搜索问题可以使用回溯法暴力搜索,只不过这次我们要做的是二维递归。
例如:77.组合(组合问题) (opens new window),131.分割回文串(分割问题) (opens new window),78.子集(子集问题) (opens new window),46.全排列(排列问题) (opens new window),以及51.N皇后(N皇后问题) (opens new window),其实这些题目都是一维递归。
包括N皇后问题,实际上也是一维递归,因为每一行只放一个皇后。因此,我们只需要一层for循环遍历一行row,递归来遍历列,然后一行一列确定皇后的唯一位置。
但是本题不一样,本题棋盘的每一个位置都要放一个数字,并检查数字是否合法。解数独的树形结构要比N皇后更宽更深。
也就是说,本题我们需要一个for循环遍历行,一个for循环遍历列,此时才能确定一个点!
确定一个点之后,递归再用来遍历这个空格,能不能放1/2/3/……9。因此,本题,我们需要两层for循环来遍历这个9*9的格子!
树形图
本题树形结构非常庞大,先画示意图大概看一下。
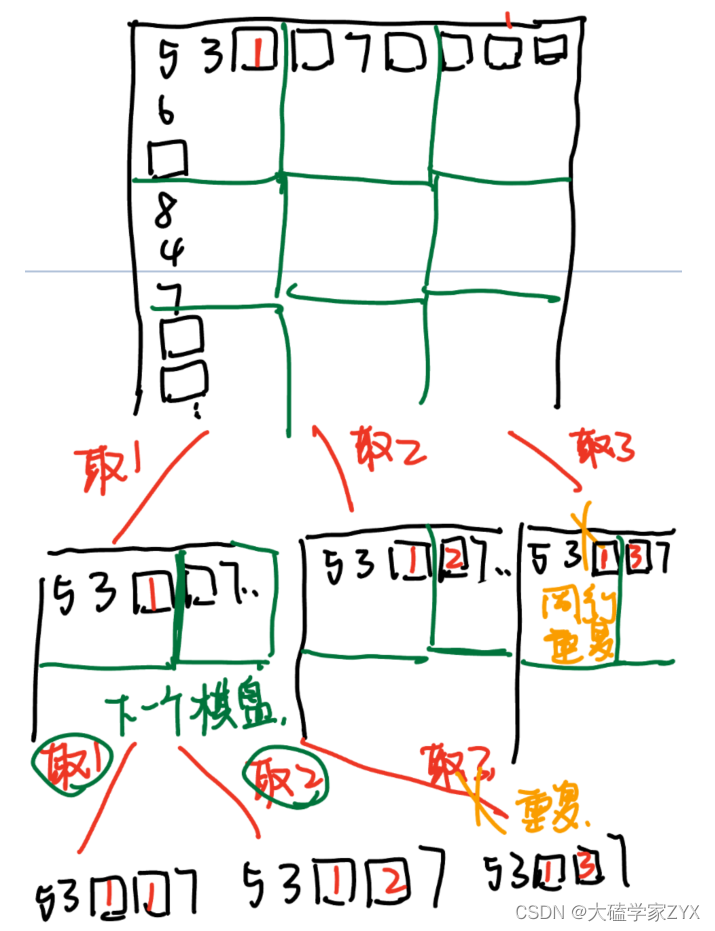
因为本题要求数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。因此,其实本题的9*9格子内还包含多个3*3的棋盘。例图里面取完了第一个格子之后,来到同行的第二个格子处理第二个棋盘。
大致逻辑就是,遍历一个空格,123456789都试一遍,如果全试过了都不满足条件,就return false。
返回值类型问题
我们之前涉及到的组合/分割/子集/排列问题,包括N皇后问题,都是有多个结果,需要用结果集把全部结果收集起来,一起返回。
多个结果意味着结果散落在树形结构里面,需要搜索整棵树,才能返回我们想要的结果。
但是本题不同,本题有一个数独就立刻返回,相当于只搜索到一个树枝的结果,就立刻返回,其他结果不搜了。因此,本题的递归函数是需要返回值的,并且返回值是bool类型,相当于做了标记,找到结果立刻返回,不需要再搜索。
搜索整个树形结构用void,搜索单个树枝用bool。
这里在代码随想录二叉树章节有讲解:代码随想录 (programmercarl.com)是路径总和这道题目,搜索单条路径用bool,搜索所有路径用void。
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。(113.路径总和ii)
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。 (236. 二叉树的最近公共祖先 )
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。(17.路径总和)
输入分析
输入:board = [[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”],[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”],[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”],[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”],[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”],[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”],[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”],[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”],[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
这个输入是一个vector<vector<char>>,因此我们想要锁定格子里的某一个空格,需要先board[i]确定是哪一行,再进入for循环遍历这一行里面的每一个元素(也就是行里的每一列)。
因此,处理每一个空格的情况,需要两层for循环锁定位置,也就是二维的递归。
回溯部分
- 因为本题只求解一个数独,因此得到一个解之后直接返回即可,因此本题递归有返回值且返回值是bool类型
- 处理逻辑:遍历一个空格,123456789都试一遍,如果全试过了都不满足条件,就return false。
- 逻辑比较复杂的题目,都是合法性判断单独写一个函数,递归的时候只进行函数调用看看该位置是不是合法。本题也是这样
bool backtracking(vector<vector<char>>&board){
//终止条件:本题有return,而且棋盘填满之后自己就会返回,所以不用终止条件
//直接开始二维递归
//行遍历
for(int i=0;i<board.size();i++){
//列遍历
for(int j=0;j<board[i].size();j++){
if(board[i][j]=='.'){
//char类型也可以向Int一样递增
for(char k='1',k<='9',k++){
//这个空格位置放k是否合法的判断
if(isValid(board,i,j,k)==true){
board[i][j]=k;
//合法才进入下层递归
//本题递归有返回值,需要接收返回值
bool result = backtracking(vector<vector<char>>&board);
//找到结果立即return ,其他树枝都不搜索!
if(result==true){
return true;
}
//回溯
board[i][j]='.';
}
}
//如果这个格子,9个数都不行,就return false
return false;
}
}
}
//如果遍历完了没有return false,那么应该return true
return true;
}
return true放最后的逻辑
Q:backtracking 的结果是 true,直接返回 true的前提,不是第一个true会产生吗?这样的情况下,第一个true如何产生?
A:当调用 backtracking 函数时,它会尝试填充第一个空格,然后调用自身来填充下一个空格,依此类推,直到找到一个完全符合数独规则的解决方案,此时返回 true。如果在尝试填充任何空格时都找不到解决方案,那么它会返回 false,并回溯到上一步,尝试填充上一个空格的下一个可能的值。
假设遍历到了最后,棋盘只有最后一个位置没有填满,此时调用 backtracking(board),并在这个位置上找到一个合法的数字填入后,将会再次调用 backtracking(board) 进行递归。
当这次递归开始的时候,棋盘已经填满了(也就是if(board[i][j] == '.')不会再执行了!),因此,这次调用会跳过所有的外层和内层循环,直接执行到最后的 return true;。这个 “true” 就是 “第一个true”。
也就是说,当棋盘填满的时候,return false语句就不会执行了(因为return false语句写在if棋盘没满的语句块最后),直接进行return true。这样也做到了类似终止条件的效果!
为什么char类型也能像int一样递增
在C++中,char类型实际上是一种整数类型,只不过它通常用于表示ASCII字符。
char类型的变量在内存中存储的是字符对应的ASCII值,例如字符’1’对应的ASCII值是49,字符’2’对应的ASCII值是50,以此类推。
当我们对一个char类型的变量进行加法操作时,实际上是在对这个变量的ASCII值进行加法操作。例如,如果有一个char变量k,其值为’1’,当执行k++时,k的ASCII值会增加1,变成50,对应的字符就是’2’。
凡是int可以进行的操作,char都可以进行。
详情见博客:
https://blog.csdn.net/CFY1226/article/details/131444907?spm=1001.2014.3001.5502
回溯的另一种写法
- 这种写法是在开头写终止条件,判断棋盘是不是还有空格,没有空格就说明满了,直接return true
- 这种写法相对好理解一些,但是开头两个for循环增加了一些时间复杂度。但是,解数独问题本身时间复杂度已经很高,两层for循环的O(mn)复杂度并不会影响总体!
bool backtracking(vector<vector<char>>&board){
// 终止条件:检查棋盘是否已经被填满
bool isFull = true;
//这里相当于两层for循环
for(const auto &row : board) {
if(std::find(row.begin(), row.end(), '.') != row.end()) {
isFull = false;
break;
}
}
if(isFull) {
return true;
}
// 剩余的递归和回溯过程
// 行遍历
for(int i=0;i<board.size();i++){
// 列遍历
for(int j=0;j<board[i].size();j++){
if(board[i][j]=='.'){
// char类型也可以向Int一样递增
for(char k='1';k<='9';k++){
// 这个空格位置放k是否合法的判断
if(isValid(board,i,j,k)==true){
board[i][j]=k;
// 合法才进入下层递归
// 本题递归有返回值,需要接收返回值
bool result = backtracking(board);
// 找到结果立即return ,其他树枝都不搜索!
if(result==true){
return true;
}
// 回溯
board[i][j]='.';
}
}
// 如果这个格子,9个数都不行,就return false
return false;
}
}
}
}
for(const auto &row : board)含义
auto 关键字用于自动推导变量的类型。在这个例子中,auto 会被编译器自动推导为 vector<char>,因为 board 是一个 vector<vector<char>> 类型的变量,所以 row 是其中的一个 vector<char>。
const 关键字表示这个变量是常量,不可以被修改。在这个例子中,我们没有任何修改 row 的操作,所以我们可以将 row 声明为 const,这样可以提高程序的安全性,避免不小心修改了 row。
& 关键字表示引用。如果没有 &,那么在每次循环中,board 的每一行都会被复制一份给 row,这会增加额外的开销。通过使用引用,我们可以避免这种复制,提高程序的效率。同时,因为 row 是 const,我们也不用担心会不小心修改了 board。
const auto &row : board 的意思是:在 board 的每一行上执行循环,每次循环中,row 是对当前行的一个常量引用。
时间复杂度问题
第二个版本开头的判断代码相当于两层 for 循环。但是并不影响总体的时间复杂度。
解决数独的问题本身的时间复杂度是 O(9^(m*n)),其中 m 和 n 是棋盘的行数和列数,也就是9^81。这是因为每个空格有9个可能的选择(1-9),并且需要搜索所有的可能性。
首先,让我们看看较容易理解的第二个版本。在主递归结构(也就是三个嵌套的for循环)之前,添加了一个检查棋盘是否已满的过程。这个过程包含两个for循环,因此它的时间复杂度是 O(m*n)。
然而,即使这个过程每次递归都会执行,它的时间复杂度仍然远远小于主递归结构的时间复杂度。因此,第一个版本的总体时间复杂度仍然是 O(9^(mn))。
对于第一个版本,它的时间复杂度也是 O(9^(m*n))。这是因为它的主递归结构与第一个版本完全相同,只是没有了检查棋盘是否已满的过程,直接return true了。
总的来说,尽管这两个版本在实现上有些不同,但他们的时间复杂度都是 O(9^(m*n))。这意味着,对于一个给定的数独问题,这两个版本的算法都会在相似的时间内找到解决方案(假设他们都找到了解决方案)。
合法性判断部分
判断棋盘是否合法有如下三个维度:
- 同行是否重复
- 同列是否重复
- 9宫格里是否重复
九宫格的判断方式
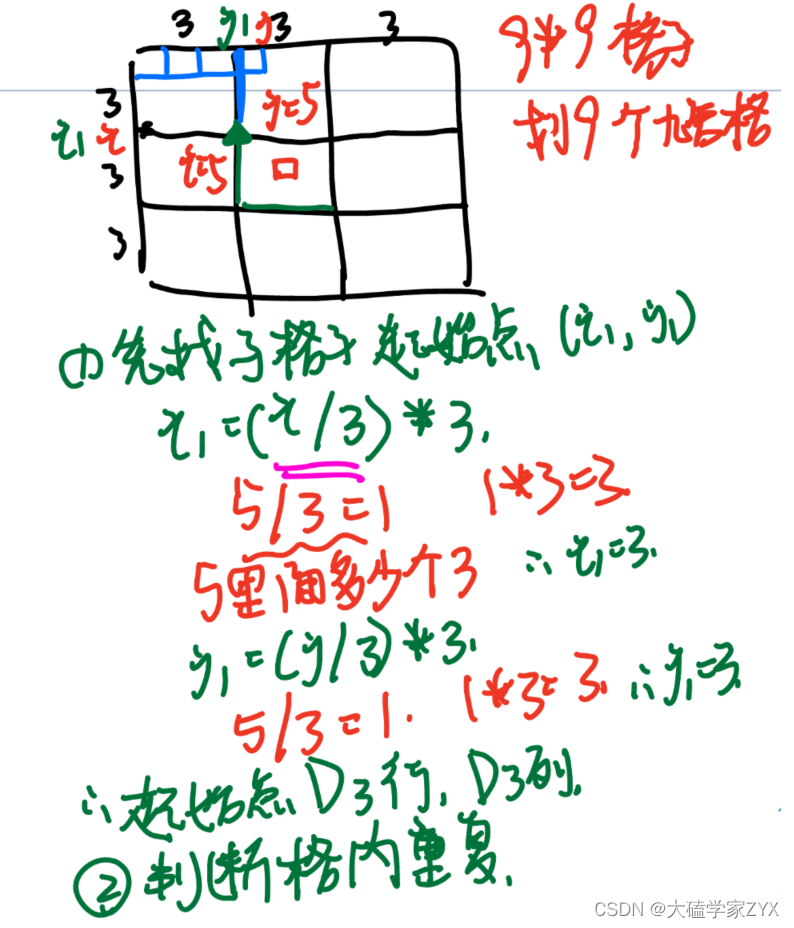
原题目是规定了9*9的格子里,九宫格的划分方式。需要在已经划分好的九宫格内部进行判断。

因此,九宫格内部的去重判断,只需要找到目前元素[row,col]属于哪个子格子,这个子格子的起始点是第几行第几列就可以了!
判断逻辑如图。
注意:取余运算和取模运算
- 取3余的目的就是为了得知这个数字里有几个3!例如图中行号5对3取余,5/3=1,也就是说5里面有一个3,这个子格子的*起始点行号应该是5/3 3 !
- 一定要注意区分取余和取余数的区别,取余/结果是商,不是余数!如果想要得到余数,我们应该用取模运算符%,例如5%3=2。但是本题并不需要取模,我们只需要对3取余,看有几个3就能确定子格子的起始行号!
- 例如i=5的情况,其所在的格子,起始点是本行的第四个格子,而不是第三个,所以下标为3是正确的,不用-1。
bool isValid(vector<vector<char>>&board,int row,int cal,char val){
//判断同行是否重复
for(int i=0;i<9;i++){
if(board[row][i]==val){
return false;
}
}
//同列
for(int j=0;j<9;j++){
if(board[j][cal]==val){
return false;
}
}
//同九宫格,这里一定要画个图看看,才能搞清楚下标和边界条件
int startRow = (row/3)*3;
int startCol = (col/3)*3;
for(int i=startRow;i<startRow+3;i++){
for(int j=startCol;j<startCol+3;j++){
if(board[i][j]==val){
return false;
}
}
}
//都不重复
return true;
}
- 注意取模和取余的问题,本题选择取余,因为并不需要知道当前格子位置,只需要判断当前格子属于的子格子的起始点!!
- 注意下标的问题,本题中中间的子格子也是从第四个格子开始,所以也不存在下标-1的问题
- 遇到九宫格这种问题一定要画图!画图才能看清楚下标!
完整版
class Solution {
public:
bool isValid(vector<vector<char>>&board,int row,int col,char val){
//同行同列
for(int i=0;i<board.size();i++){
if(board[row][i]==val) return false;
}
for(int j=0;j<board.size();j++){
if(board[j][col]==val) return false;
}
//九宫格
int startRow = (row/3)*3;
int startCol = (col/3)*3;
for(int i=startRow;i<startRow+3;i++){
for(int j=startCol;j<startCol+3;j++){
if(board[i][j]==val) return false;
}
}
return true;
}
//只搜索一条路径即可,所以需要返回值
bool backtracking(vector<vector<char>>& board){
//终止条件可以不写
//单层搜索
for(int i=0;i<board.size();i++){
for(int j=0;j<board[i].size();j++){
if(board[i][j]=='.'){
for(char num='1';num<='9';num++){
if(isValid(board,i,j,num)==true){
board[i][j]=num;
bool result = backtracking(board);
if(result==true){
return true;
}
board[i][j]='.';
}
}
return false;
}
}
}
return true;
}
void solveSudoku(vector<vector<char>>& board) {
backtracking(board);
}
};
为什么本题递归不传入i+1或j+1参数?
在这个具体的数独解题程序中,每次递归调用backtracking(board)函数时,都会从整个棋盘的左上角开始遍历。虽然在一个递归层次中找到一个可以填入数字的空格并填入后,下一次递归调用依然从棋盘的左上角开始,但实际上已经填入数字的位置在后续递归中都会被跳过。
这种方法的好处是代码逻辑简洁清晰,每次处理都是在整个棋盘上进行,不需要维护当前遍历到的具体位置。尽管存在一定的性能损失(因为需要反复遍历已经处理过的位置),但由于数独棋盘的规模较小(9x9),因此这种性能损失在实际运行中并不明显。
当然,也可以选择优化这部分逻辑,通过显式地维护当前处理到的位置(比如使用i和j作为参数传入递归函数),从而避免反复遍历已处理过的位置。这样可以进一步提高程序的运行效率,但同时也会增加代码的复杂度。
也就是说,从左上角开始遍历确实会有一些性能损失,但因为数独棋盘的大小是固定的(9x9),所以这种方法的时间复杂度是可以接受的。
优化尝试:每次递归不遍历整个棋盘
如果想优化这个算法,可以使用一个方法来显式地追踪当前的位置,从而避免反复遍历已经填入数字的格子。
一个可能的方法是将当前的行和列作为额外的参数传入 backtracking 函数。这样,可以从最后填入数字的地方开始遍历,而不是从棋盘的左上角开始。
bool backtracking(vector<vector<char>>& board, int row, int col) {
// Check if we have reached the end of the board
if (row == 9) {
return true;
}
// Check if we have reached the end of the row
if (col == 9) {
return backtracking(board, row + 1, 0);
}
// Skip the cells that are already filled
if (board[row][col] != '.') {
return backtracking(board, row, col + 1);
}
for (char num = '1'; num <= '9'; num++) {
if (isValid(board, row, col, num)) {
board[row][col] = num;
if (backtracking(board, row, col + 1)) {
return true;
}
// undo the choice for the next exploration
board[row][col] = '.';
}
}
return false;
}
在优化后的代码中,我们没有显式地在代码中写出第二个for循环。然而,我们通过递归调用 backtracking(board, row, col + 1) 创建了一个隐式的列遍历循环。当我们遍历到棋盘上的一个新列时,我们会进行一次新的递归调用来继续解数独。当我们达到一行的末尾时(即 col == 9),我们会开始遍历下一行,这是通过递归调用 backtracking(board, row + 1, 0) 实现的。
所以,尽管在代码中只看到了一个显式的循环(即遍历1-9的数字),实际上我们还有两个隐式的循环(行和列的遍历),它们是通过递归调用实现的。这样的设计使得我们可以在遍历每一行的同时,跳过已经填入数字的格子,这样可以避免了原始版本的代码中的一些重复遍历。
但是这种优化实际上没什么意义,时间复杂度不变,但是代码复杂性提升了很多。
时间复杂度
优化版本的算法的时间复杂度和原始版本的算法相比并没有明显的差别。
因为都是在最坏情况下需要遍历数独棋盘上的所有可能的数字配置,所以它们的时间复杂度都是 O(9^(n*n)),其中 n 是数独棋盘的边长(在这个例子中,n=9)。然而,由于优化版本的算法减少了重复的遍历,所以在实际的运行中,它可能会比原始版本的算法更快一些。
值得注意的是,虽然优化版本的算法可以减少一些不必要的计算,但同时也增加了代码的复杂度。在很多情况下,简洁清晰的代码比微小的性能优化更重要。在选择优化策略时,需要根据具体的应用场景和需求来做决定。