1、训练误差和泛化误差

训练误差（training error）是指， 模型在训练数据集上计算得到的误差。 泛化误差（generalization error）是指， 模型对位置数据项预测的误差，泛化误差体现出了模型的泛化能力。

2、模型复杂性

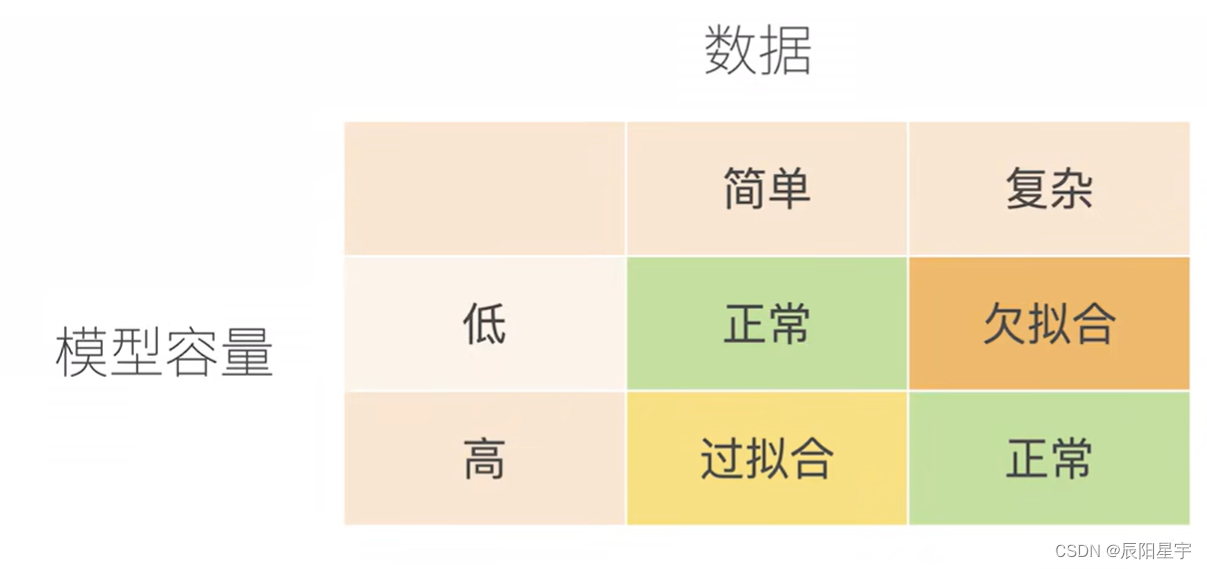
当我们有简单的模型和大量的数据时，我们期望泛化误差与训练误差相近。 当我们有更复杂的模型和更少的样本时，我们预计训练误差会下降，但泛化误差会增大。 模型复杂性由什么构成是一个复杂的问题。

一个模型是否能很好地泛化取决于很多因素。 例如，具有更多参数的模型可能被认为更复杂， 参数有更大取值范围的模型可能更为复杂。 通常对于神经网络，我们认为需要更多训练迭代的模型比较复杂， 而需要早停（early stopping）的模型（即较少训练迭代周期）就不那么复杂。

我们很难比较本质上不同大类的模型之间（例如，决策树与神经网络）的复杂性。 就目前而言，一条简单的经验法则相当有用： 统计学家认为，能够轻松解释任意事实的模型是复杂的， 而表达能力有限但仍能很好地解释数据的模型可能更有现实用途。

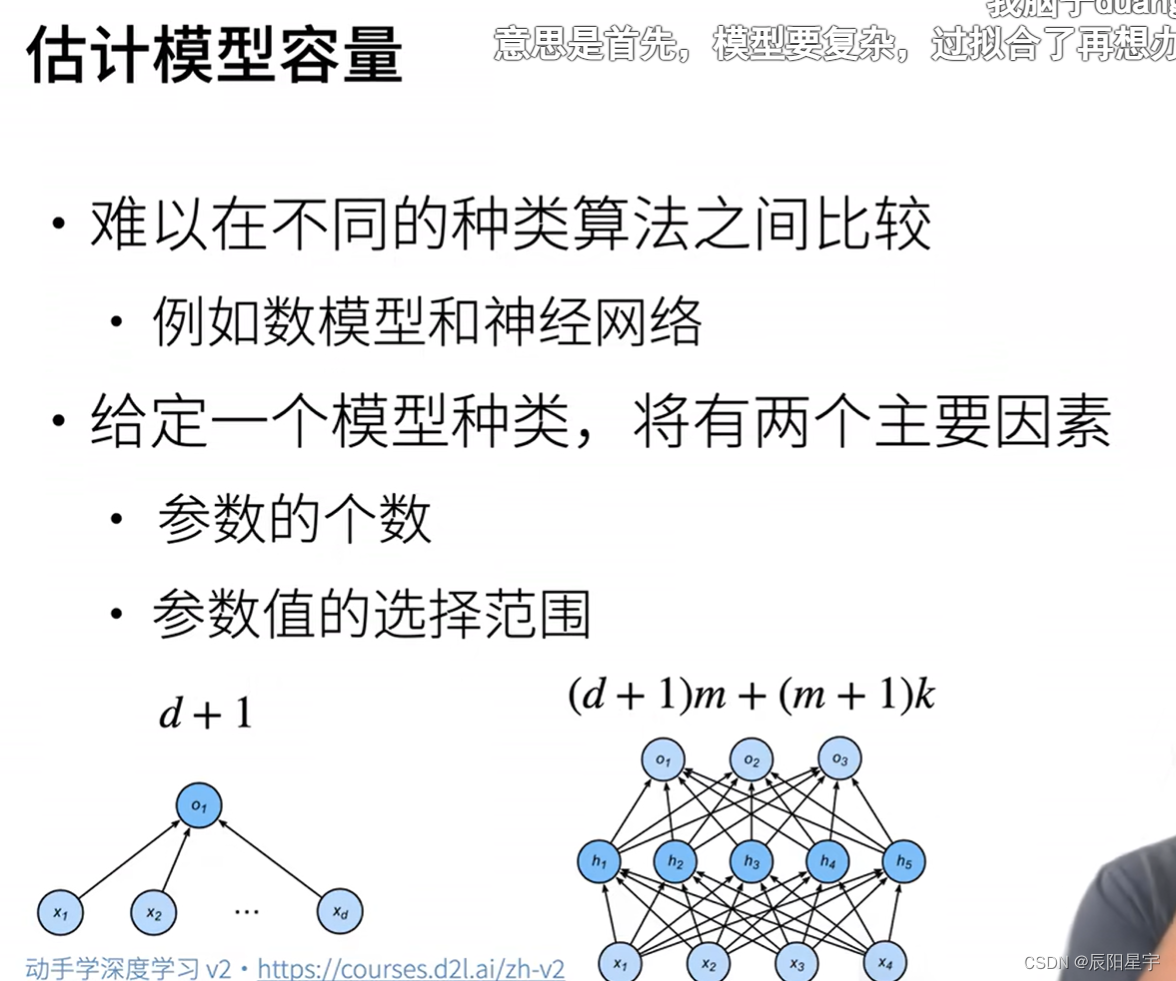
泛化性的影响因素：

1. 可调整参数的数量。当可调整参数的数量（有时称为自由度）很大时，模型往往更容易过拟合。
2. 参数采用的值。当权重的取值范围较大时，模型可能更容易过拟合。
3. 训练样本的数量。即使模型很简单，也很容易过拟合只包含一两个样本的数据集。而过拟合一个有数百万个样本的数据集则需要一个极其灵活的模型。

为了说明一些关于过拟合和模型复杂性的经典直觉，我们给出一个多项式的例子。给定由单个特征$x$和对应实数标签$y$组成的训练数据，我们试图找到下面的$d$阶多项式来估计标签$y$。

$$\hat{y}=\sum _{i=0}^d{x}^i{w}_i$$

这只是一个线性回归问题，我们的特征是$x$的幂给出的，模型的权重是$w_i$给出的，偏置是$w_0$给出的（因为对于所有的$x$都有$x^0=1$）。由于这只是一个线性回归问题，我们可以使用平方误差作为我们的损失函数。

高阶多项式函数比低阶多项式函数复杂得多。高阶多项式的参数较多，模型函数的选择范围较广。因此在固定训练数据集的情况下，高阶多项式函数相对于低阶多项式的训练误差应该始终更低（最坏也是相等）。事实上，当数据样本包含了$x$的不同值时，函数阶数等于数据样本数量的多项式函数可以完美拟合训练集。

我们直观地描述了多项式的阶数和欠拟合与过拟合之间的关系。

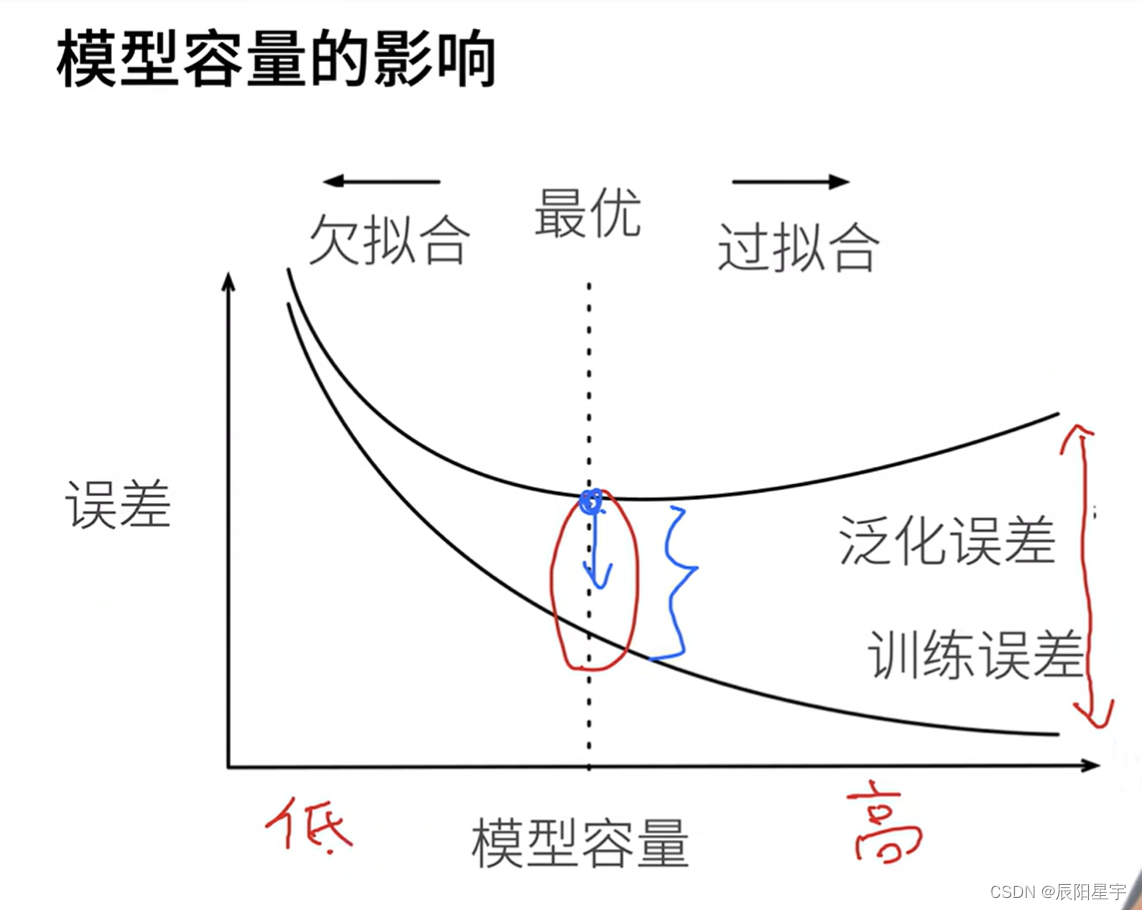
将模型在训练数据上拟合的比在潜在分布中更接近的现象称为过拟合（overfitting）， 用于对抗过拟合的技术称为正则化（regularization）。 当模型在测试数据上拟合的误差过大时，称为欠拟合（underfitting），解决方法是增加模型复杂度，增加训练数据量。

3、数据复杂性

训练数据集中的样本越少，我们就越有可能（且更严重地）过拟合。 随着训练数据量的增加，泛化误差通常会减小。 此外，一般来说，更多的数据不会有什么坏处。 对于固定的任务和数据分布，模型复杂性和数据集大小之间通常存在关系。 给出更多的数据，我们可能会尝试拟合一个更复杂的模型。 能够拟合更复杂的模型可能是有益的。 如果没有足够的数据，简单的模型可能更有用。 对于许多任务，深度学习只有在有数千个训练样本时才优于线性模型。 从一定程度上来说，深度学习目前的生机要归功于 廉价存储、互联设备以及数字化经济带来的海量数据集。

1. 模型验证集

在我们确定所有的超参数之前，我们不希望用到测试集。 如果我们在模型选择过程中使用测试数据，可能会有过拟合测试数据的风险，那就麻烦大了。我们决不能依靠测试数据进行模型选择。 然而，我们也不能仅仅依靠训练数据来选择模型，因为我们无法估计训练数据的泛化误差。

解决此问题的常见做法是将我们的数据分成三份， 除了训练和测试数据集之外，还增加一个验证数据集（validation dataset）， 也叫验证集（validation set）。 但现实是验证数据和测试数据之间的边界模糊得令人担忧。

我们将数据分为三份，分别是：训练集、验证集和测试集。用训练集训练数据，用验证集确定模型参数，最后用测试机来评估模型性能。一般分配比例为0.6:0.2:0.2。

2. K折交叉验证

当训练数据稀缺时=，我们甚至可能无法提供足够的数据来构成一个合适的验证集。 这个问题的一个流行的解决方案是采用K折交叉验证。 这里，原始训练数据被分成K个不重叠的子集。 然后执行K次模型训练和验证，每次在K-1个子集上进行训练， 并在剩余的一个子集（在该轮中没有用于训练的子集）上进行验证。

4、多项式回归探索模型和数据

我们现在可以通过多项式拟合来探索这些概念。

import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l

1. 生成数据集

给定$x$，我们将使用以下三阶多项式来生成训练和测试数据的标签：
$$y=5+1.2x-3.4\frac{x^2}{2!}+5.6\frac{x^3}{3!}+ϵ\text{ where }ϵ\sim \mathcal{N}(0,0.1^2).$$

噪声项$ϵ$服从均值为0且标准差为0.1的正态分布。

在优化的过程中，我们通常希望避免非常大的梯度值或损失值。这就是我们将特征从$x^i$调整为$\frac{x^i}{i!}$的原因，这样可以避免很大的$i$带来的特别大的指数值。我们将为训练集和测试集各生成100个样本。

max_degree = 20  # 多项式的最大阶数
n_train, n_test = 100, 100  # 训练和测试数据集大小
true_w = np.zeros(max_degree)  # 分配大量的空间
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])

features = np.random.normal(size=(n_train + n_test, 1))		# 生成数据集
np.random.shuffle(features)									# 进行随机打乱
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))		
for i in range(max_degree):
    poly_features[:, i] /= math.gamma(i + 1)  # gamma(n)=(n-1)!
# labels的维度:(n_train+n_test,)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)

（1）poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))：
首先，np.arange(max_degree)生成一个从0到max_degree-1的数组，然后通过reshape(1, -1)将其转换为一个1行max_degree列的矩阵，这个矩阵表示了多项式的指数部分。
接下来，np.power(features, np.arange(max_degree).reshape(1, -1))将特征矩阵的每个元素与指数矩阵对应元素进行幂运算。这样得到的矩阵的每一列代表了一个特征的多项式展开。

（2）for循环：
通过循环遍历每一列，将多项式矩阵的每个元素除以math.gamma(i + 1)。这里使用了math.gamma()函数来计算阶乘。这一步的目的是对多项式进行归一化，使得每一项的系数都在合理的范围内。

同样，存储在poly_features中的单项式由gamma函数重新缩放，其中$\Gamma (n)=(n-1)!$。从生成的数据集中查看一下前2个样本，第一个值是与偏置相对应的常量特征。

# NumPy ndarray转换为tensor
true_w, features, poly_features, labels = 
[torch.tensor(x, dtype=torch.float32) 
for x in [true_w, features, poly_features, labels]]

2. 多模型进行训练和测试

首先让我们实现一个函数来评估模型在给定数据集上的损失。

def evaluate_loss(net, data_iter, loss):  #@save
    """评估给定数据集上模型的损失"""
    metric = d2l.Accumulator(2)  # 损失的总和,样本数量
    for X, y in data_iter:
        out = net(X)
        y = y.reshape(out.shape)
        l = loss(out, y)
        metric.add(l.sum(), l.numel())
    return metric[0] / metric[1]

定义训练函数

def train(train_features, test_features, train_labels, test_labels,
          num_epochs=400):
    loss = nn.MSELoss(reduction='none')
    input_shape = train_features.shape[-1]
    # 不设置偏置，因为我们已经在多项式中实现了它
    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
    batch_size = min(10, train_labels.shape[0])
    train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),
                                batch_size)
    test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),
                               batch_size, is_train=False)
    trainer = torch.optim.SGD(net.parameters(), lr=0.01)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
                            xlim=[1, num_epochs], ylim=[1e-3, 1e2],
                            legend=['train', 'test'])
    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
                                     evaluate_loss(net, test_iter, loss)))
    print('weight:', net[0].weight.data.numpy())

3. 拟合情况

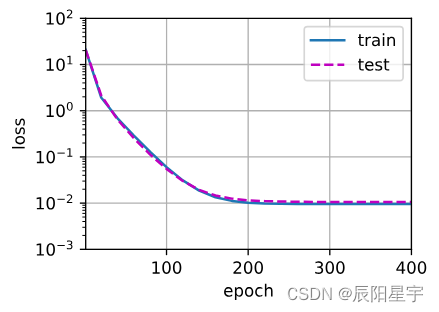
（1）三阶多项式函数拟合(正常)

# 从多项式特征中选择前4个维度，即1,x,x^2/2!,x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
      labels[:n_train], labels[n_train:])

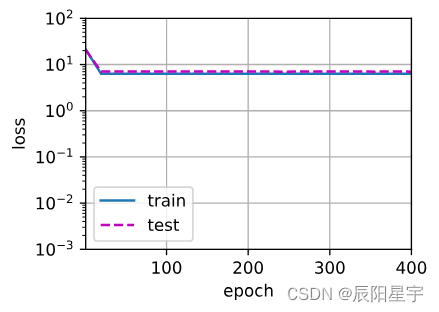
（2）线性函数拟合(欠拟合)

# 从多项式特征中选择前2个维度，即1和x
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
      labels[:n_train], labels[n_train:])

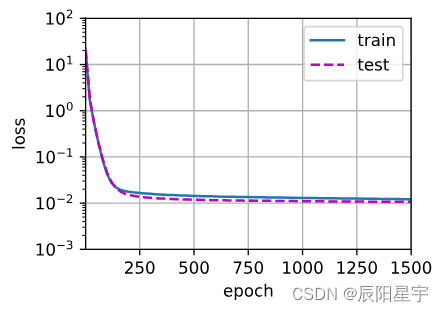
（3）高阶多项式函数拟合(过拟合)

# 从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:, :],
      labels[:n_train], labels[n_train:], num_epochs=1500)

参考文章：4.4. 模型选择、欠拟合和过拟合