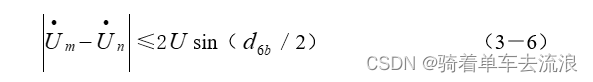算法介绍

我们前一天写了一道桶排序，今天开始看它的进化版：基数排序，为啥会有这个算法呢?因为我们桶排序有一部是需要统计每个数字出现的次数因此需要开一个相对大的数组

for(int i=0;i<n;i++){
        s[q[i]]++; 
    }

但是就像快速排序这道题，它的数值到了10的9次方了，咋映射呢？总不可能再开这么大一个数组吧？会溢出的。那咋办呢？于是就有了基数排序。

那么基数排序是啥意思呢？这个基数其实是指的进制中的基数，我们所做的其实就是将原本10进制的数转换为以r为基数的进制也就是r进制，然后再作比较。但是也并不是就直接排序，而是每个位进行排序：

举个例子：321 456 789 123 341 这五个数排序，那么基数排序的过程就是从低位向高位开始排，也就是根据最低位(个位)排序：321 341 123 456 789 然后根据10位排序：321 123 341 456 789然后根据百位排序：123 321 341 456 789 这样就排好了。当然这个例子是易于理解的，因为我们只是将10进制转换到了10进制而已，但是是每个位上比较(这样每一位上做投影就不需要开那么大的数组)。

算法题目

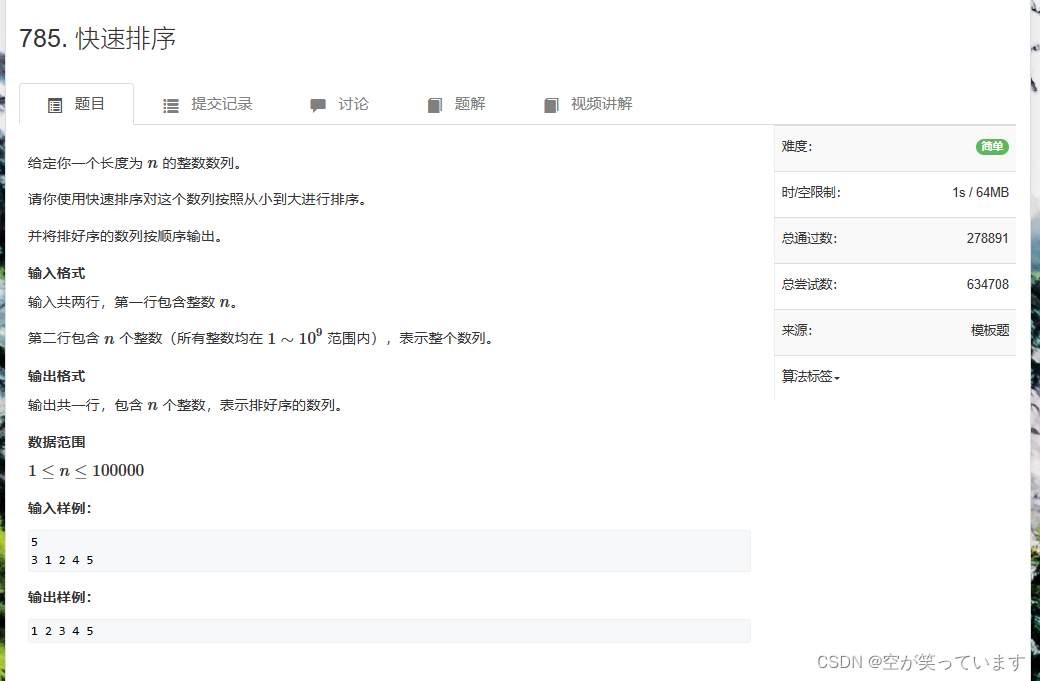
ac代码：

#include <iostream>

using namespace std;

const int N = 1000010;
int q[N], w[N],s[N];
//第一位参数d:根据参数大小和进制大小确定需要多少位
//第二位参数r:进制的基数。
void radix_sort(int d,int r,int n){
     int radix = 1;
     for(int i=1;i<=d;i++){
         for(int j=0;j<r;j++) s[j]=0;
         for(int j=0;j<n;j++) s[q[j]/radix%r]++;
         for(int j=1;j<r;j++) s[j] = s[j-1] + s[j];
         for(int j=n-1;j>=0;j--) w[--s[q[j]/radix%r]] = q[j];
        //  for(int j=1;j<n;j++) w[--s[q[j]/radix%r]] = q[j];
        //被注释这一行，如果按照这样写就是从大到小排序
         for(int i=0;i<n;i++) q[i] = w[i];
         radix = radix * r;
     }
    return;
}
int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++)scanf("%d",&q[i]);
    radix_sort(5,100,n);
    for(int i=0;i<n;i++)printf("%d ",q[i]);
    return 0;
}