一、单向循环链表

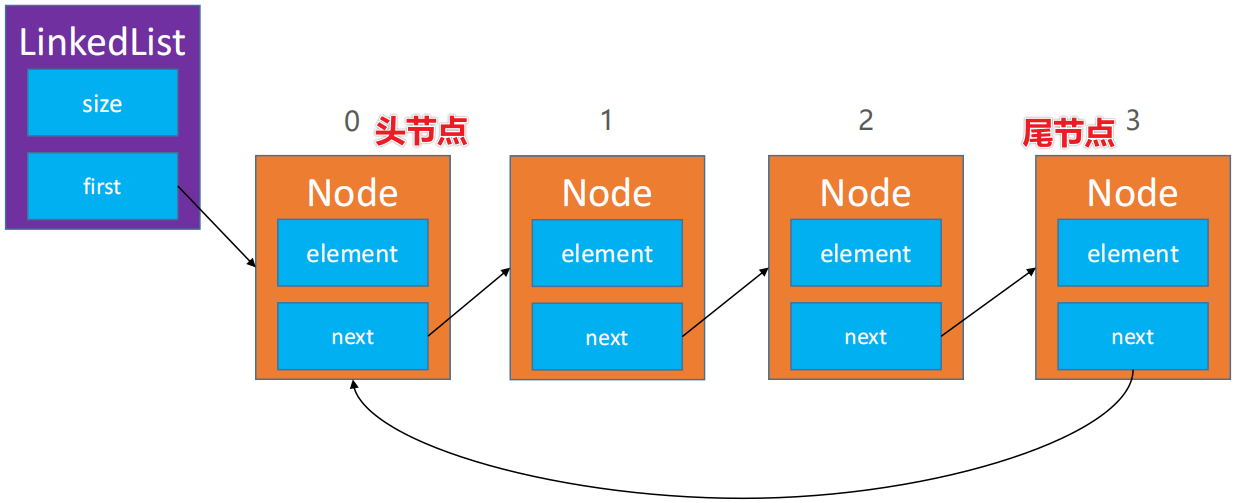
🌿 单向循环链表在单链表的基础上，尾节点的 next 指向头节点

(1) add()

🌿 只用考虑添加头节点的情况
🌿 要考虑一个节点都没有，插入第一个节点的情况

  @Override
  public void add(int index, E element) {
      rangeCheck4Add(index);

      if (index == 0) { // 把元素插入到头节点的位置
          Node<E> head = new Node<>(element, first);

          // 拿到尾节点
          Node<E> tail = (size == 0) ? head : node(size - 1);
          tail.next = head;
          first = head; // 头指针指向头节点
      } else {
          // 拿到【index - 1】位置的节点
          Node<E> prev = node(index - 1);
          prev.next = new Node<>(element, prev.next);
      }

      size++;
  }

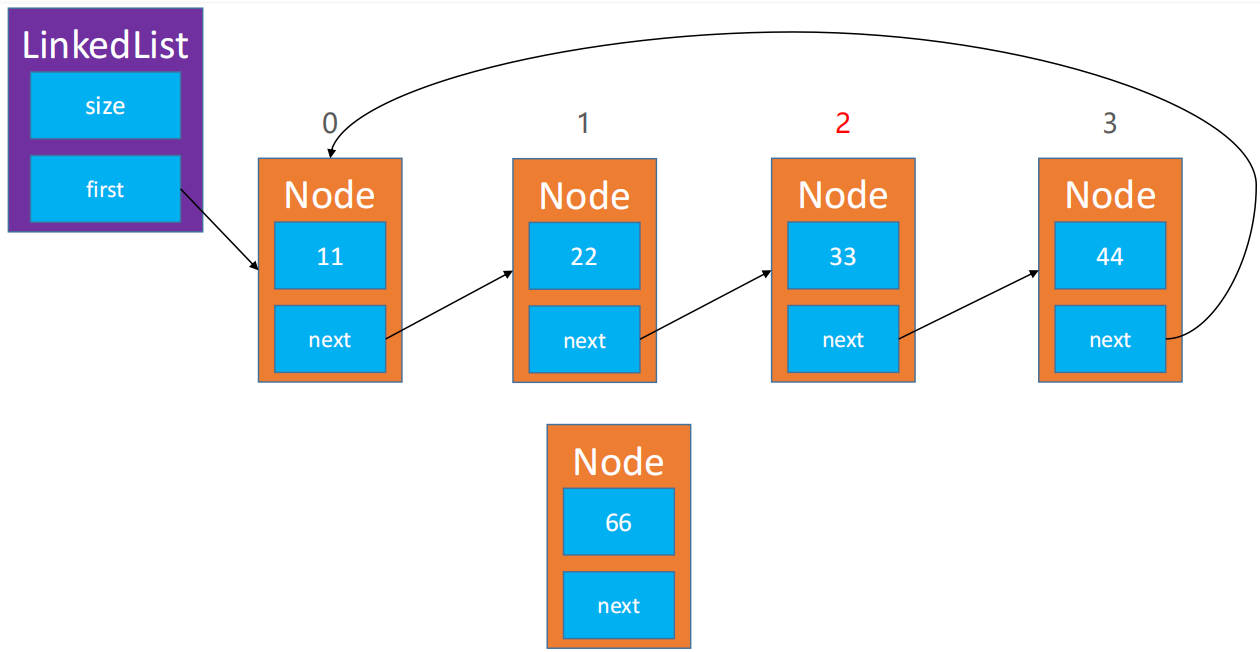
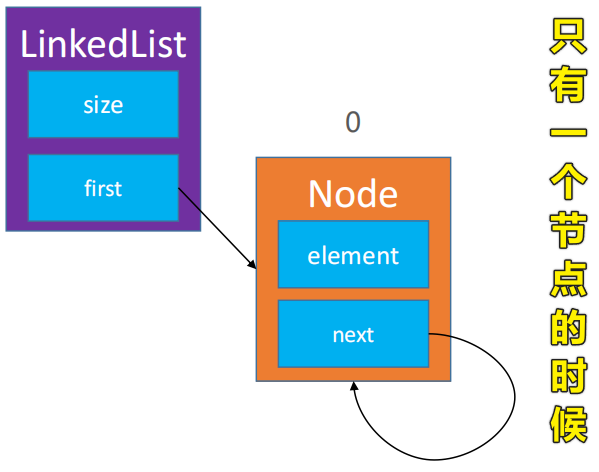
🌿 假如链表中一个节点都没有的时候，插入的第一个节点的 next 指向它本身

(2) remove()

🌿 只用考虑删除头节点的情况
🌿 假如只有一个节点，且要删除该节点的时候，只需要让头指针 first 指向为 null 即可

  @Override
  public E remove(int index) {
      rangeCheck(index);

      Node<E> node = first;

      if (index == 0) { // 删除头节点
          if (size == 1) {
              first = null;
          } else {
              // 拿到尾节点
              // node() 方法中使用到了 first 头指针
              Node<E> tail = node(size - 1);

              first = node.next;
              // 尾节点指向头节点
              tail.next = first;
          }
      } else {
          Node<E> prev = node(index - 1);
          node = prev.next;

          prev.next = node.next;
      }

      size--;

      return node.element;
  }

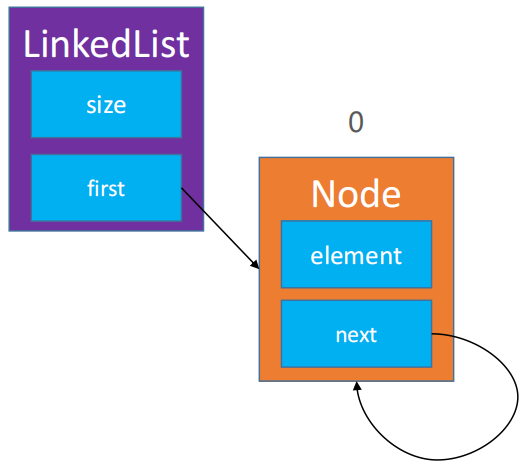
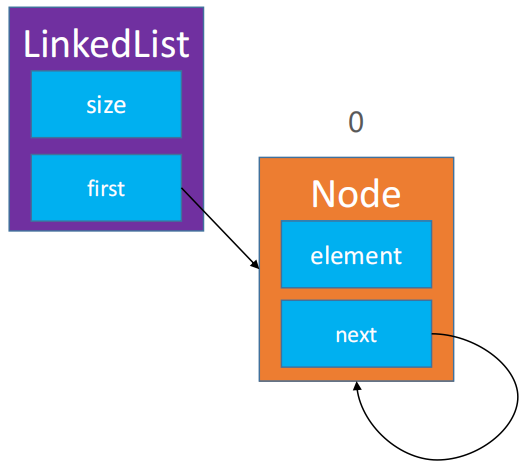
🌿 当要删除的链表中只有一个节点的时候，直接让头指针 first 等于 null

(3) 单向循环链表特点

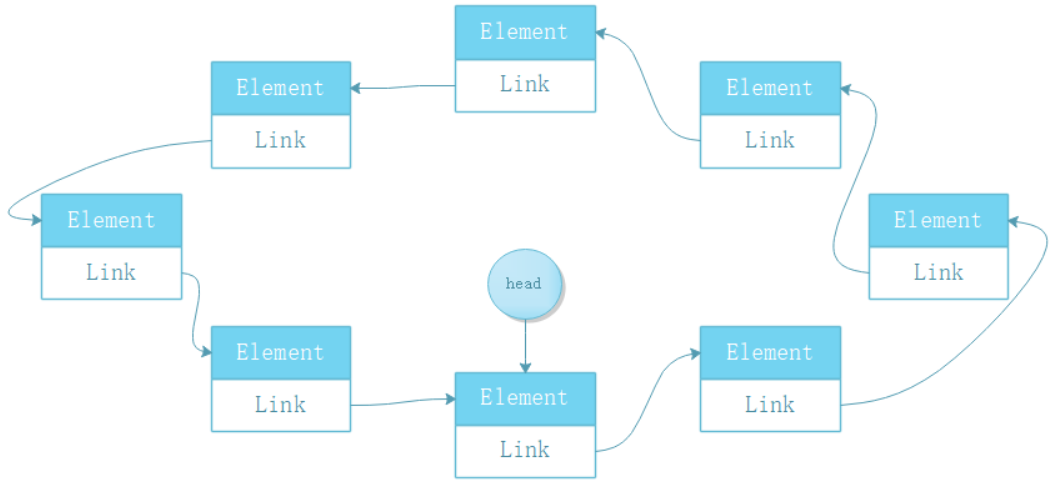
🌱 相比单链表的尾节点的 next 指向 null 而言，单向循环链表的尾节点的 next 是指向头节点
🌱 这样一来的话，从单向循环链表的任意一个节点出发都可以获取到整个链表中的全部节点

二、双向循环链表

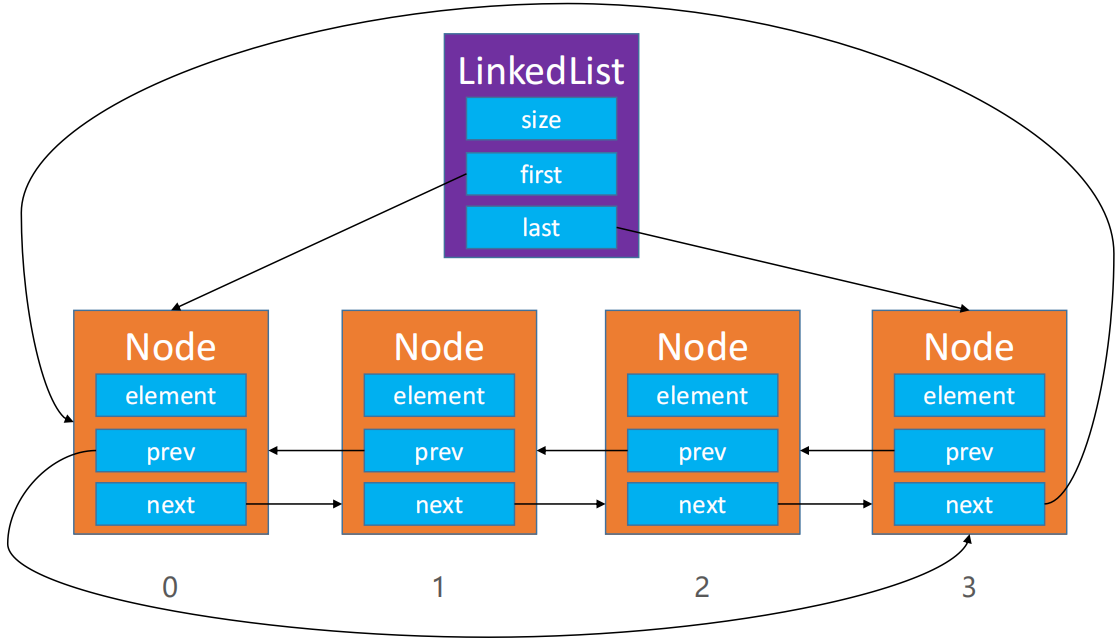
🍀 双向循环链表本身也是双向链表
🍀 双向循环链表的头节点的 prev 指向尾节点
🍀 双向循环链表的尾节点的 next 指向头节点

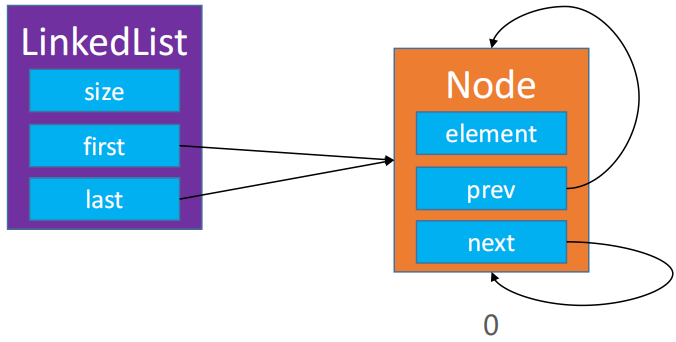
代码太恶心了： 🤮🤧

/**
 * 双向循环链表
 */
public class DoubleCircleLinkedList<E> extends AbstractList<E> {
    private Node<E> first; // 头指针
    private Node<E> last; // 尾指针

    @Override
    public E get(int index) {
        return node(index).element;
    }

    @Override
    public E set(int index, E element) {
        Node<E> node = node(index);
        E old = node.element;
        node.element = element;
        return old;
    }

    @Override
    public void add(int index, E element) {
        rangeCheck4Add(index);

        if (size == 0 || (first == null && last == null)) { // 添加第一个节点
            Node<E> head = new Node<>(element, null, null);
            head.prev = head;
            head.next = head;
            first = last = head;
        } else {
            if (index == size) { // 往最后插入新节点
                Node<E> oldLast = last;
                last = new Node<>(element, oldLast, null);
                oldLast.next = last;
                // 新节点的 next 指向头节点
                last.next = first;
                // 头节点的  prev 指向新节点
                first.prev = last;
            } else {
                Node<E> next = node(index);
                Node<E> prev = next.prev;
                Node<E> newNode = new Node<>(element, prev, next);

                next.prev = newNode;
                prev.next = newNode;

                if (index == 0) {
                    first = newNode; // 头指针指向新节点
                }
            }
        }

        size++;
    }

    @Override
    public E remove(int index) {
        rangeCheck(index);

        Node<E> node = null;

        if (size == 1) { // 删除的链表中只有一个节点的时候
            node = first;
            first = null;
            last = null;
        } else {
            node = node(index);
            Node<E> prev = node.prev;
            Node<E> next = node.next;

            prev.next = next;
            next.prev = prev;

            if (index == 0) { // 删除头节点
                first = next;
            }

            if (index == (size - 1)) { // 删除尾节点
                last = prev;
            }
        }

        size--;

        return node.element;
    }

    @Override
    public int indexOf(E element) {
        return 0;
    }

    @Override
    public void clear() {
        size = 0;
        first = null;
        last = null;
    }

    private static class Node<E> {
        E element;
        Node<E> prev;
        Node<E> next;

        Node(E element, Node<E> prev, Node<E> next) {
            this.element = element;
            this.prev = prev;
            this.next = next;
        }

        @Override
        public String toString() {
            if (prev == null) {
                return "null" + " ←【" + element + "】→ " + next.element + ", ";
            }

            if (next == null) {
                return prev.element + " ←【" + element + "】→ " + "null";
            }

            return prev.element + " ←【" + element + "】→ " + next.element + ", ";
        }
    }

    /**
     * 根据索引找节点
     */
    private Node<E> node(int index) {
        rangeCheck(index);

        if (index < (index >> 1)) { // 找左边的节点
            Node<E> node = first;
            for (int i = 0; i < index; i++) {
                node = node.next;
            }
            return node;
        } else {
            Node<E> node = last;
            for (int i = size - 1; i > index; i--) {
                node = node.prev;
            }
            return node;
        }
    }

    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        sb.append("{size=").append(size).append(", [");

        Node<E> moveNode = first;

        for (int i = 0; i < size; i++) {
            sb.append(moveNode);
            moveNode = moveNode.next;
        }

        sb.append("]}");
        return sb.toString();
    }

}

三、约瑟夫问题（Josephus Problem）

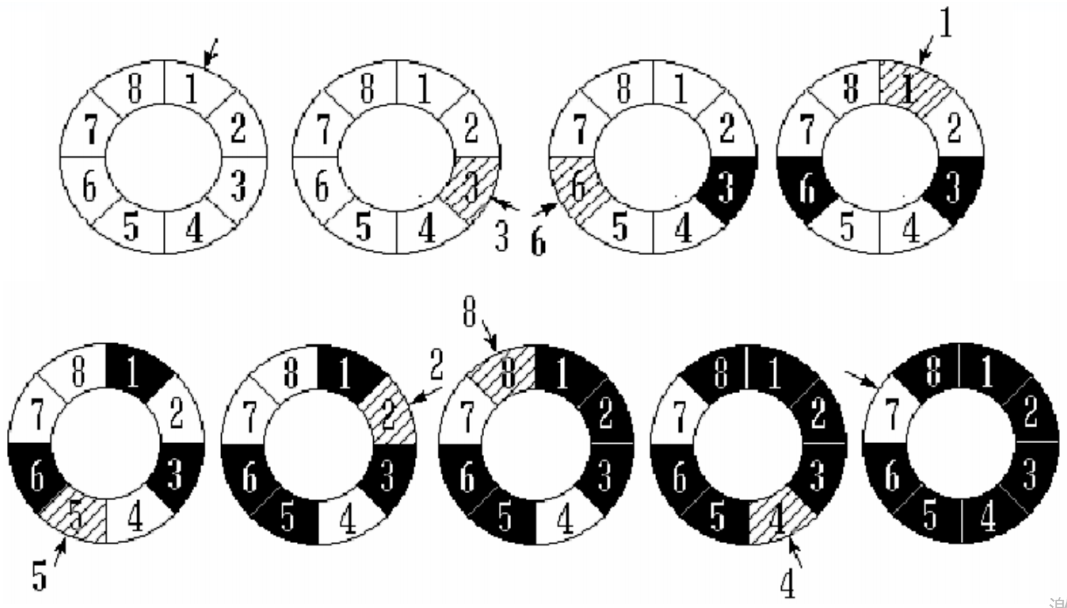
❄️ 在双向循环链表的基础上增加1个成员变量、3个方法，以便解决约瑟夫问题
❄️ current 成员变量：用于指向某个节点
❄️void reset()：让 current 指向头节点 first
❄️ E next()：让 current 往后走一步（current = current.next）
❄️E remove()：删除 current 指向的节点，删除成功后让 current 指向下一个节点，并返回被删除的节点值

四、静态链表

🌱 前面所学习的链表，是依赖于指针（引用）实现的
🌱 有些编程语言是没有指针的，比如早期的 BASIC、FORTRAN 语言

🌱 没有指针的情况下，如何实现链表？

• 可以通过数组来模拟链表，称为静态链表
• 数组的每个元素存放 2 个数据：① 值、② 下个元素的索引
• 数组 0 位置存放的是头节点信息

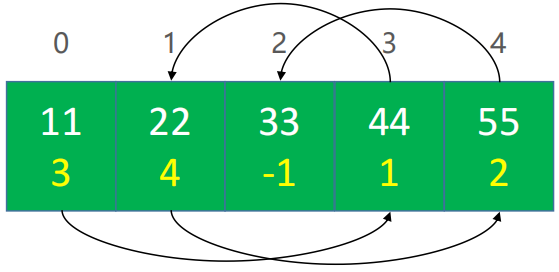
❓ 如果数组的每个元素只能存放 1 个数据呢 ❓
🌱 使用 2 个数组，1 个数组存放索引关系，1 个数组存放值

基于这种思路可以对 ArrayList 做进一步优化

---

• 我学习数据结构与算法的全部代码：https://gitee.com/zgq666good/datastructureandalgorithm.git
• 学习资料来自于我偶像 ~ 李明杰（小码哥教育）
  

🌿如有错误，请不吝赐教🌿